Logik, Geometrie

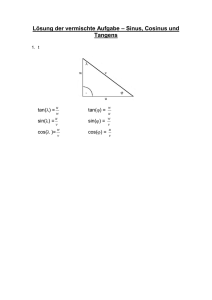
Stephan Peter
Wirtschaftsingenieurwesen WS 15/16
Mathematik
Serie 6
Logik & Geometrie
Auf einer Zugfahrt durch Schottland sitzen ein Philosoph, ein Physiker und ein Mathematiker gemeinsam in einem Eisenbahnabteil, als auf einer Wiese draußen ein schwarzes
Schaf zu sehen ist.
Philosoph: Öh! Alle schottischen Schafe sind schwarz."Physiker: "Nein! In Schottland gibt
es wenigstens ein schwarzes Schaf!"Mathematiker: "Nein, auch falsch! In Schottland gibt
es mindestens eine Wiese mit mindestens einem Schaf, das auf mindestens einer Seite
schwarz ist..."
1 Logik
Aufgabe 1
Wenn eine Aussage B aus einer Aussage A folgt, kurz: A ⇒ B, so sagt man „A ist eine
hinreichende Bedingung für B“ und „B ist eine notwendige Bedingung für A“.
Wir betrachten die Aussagen:
A ”Die Zahl n ist durch 6 teilbar.”
B ”Die Zahl n ist durch 3 teilbar.”
C ”Die Zahl n ist durch 2 teilbar.”
Welche der Aussagen ist notwendig bzw. hinreichend für die jeweils andere?
Aufgabe 2
Formulieren Sie folgende Aussagen in Worten und bestimmen Sie ihren Wahrheitswert:
a) ∀x ∈ R : x2 ≥ 1
b) ∃n ∈ N : 2n > 100
c) ∃a, b, c ∈ N : a2 + b2 = c2
d∗ ) ∀x ∈ R ∃y ∈ R : x = y 2
Aufgabe 3
Negieren Sie folgende Aussage:
Bei der letzten Ziehung der LOTTO-Zahlen war keine Zahl größer als 30.
1
2 Winkel & Bögen
Aufgabe 4
Folgende Winkel sind im Bogenmaß bzw. Gradmaß (dezimale bzw.sexagesimale Teilung)
anzugeben.
a) 217◦
b) π6
c) 175◦ 450 000
d) 270◦ 300 000
e) 300◦ 150 000
f) 175, 5◦
g) 175, 25◦
h) 175, 75◦
i) 0, 2◦
j) 0, 4◦
Aufgabe 5
Berechnen Sie die fehlenden Winkel:
(a)
(b)
Aufgabe 6
Berechnen Sie, welche Strecke man zurücklegen müsste, um auf der Erdoberfläche von
dem Punkt mit den Koordinaten (0◦ 000 000 N, 0◦ 00 000 O) (Nebenbei, wo liegt der?) nach
Berlin-Mitte (52◦ 310 1000 N, 13◦ 240 2400 O) zu laufen, indem man so lange auf dem Äquator
entlangläuft, bis man nur noch nach Norden laufen muss. Nehmen Sie die Erde als Kugel
mit einem Radius von 6371 km an. (Die Sekunden in den Koordinaten können Sie der
Einfachheit halber auch weglassen.)
Aufgabe 7
Um wieviel Grad dreht sich ein genau auf einem der Schnittpunkte der Erdeigenrotationsachse mit der Erdoberfläche stehender Mensch aufgrund der Erdrotation in einer
Stunde um die eigene Achse? Was passiert in dieser Zeit mit einem Menschen, der genau
auf dem Äquator steht?
2
3 Strahlensätze
Aufgabe 8
Zwei Geländepunkte A und B sind durch einen See getrennt (Abbildung (c)). Ihr Abstand
x soll mit Hilfe geeignet gewählter Punkte Q, R und S bestimmt werden.
Aufgabe 9
Um die Entfernung zweier Punkte zu bestimmen, von denen einer unzugänglich ist oder
zwischen denen sich ein Hindernis befindet, verfährt man nach dem in der Abbildung (d)
unten dargestellten Verfahren. a) Worauf muss man bei diesem Verfahren unbedingt achten? b) Berechne die Entfernung der Punkte A und B, wenn die folgenden Streckenlängen
vermessen wurden: m = 270m, n = 90m, a = 60m.
Aufgabe 10
Berechne die die Länge des Teichs in Abbildung (e).
Aufgabe 11
Die Dicke von dünnen Drähten kann man mit einem sogenannten ‚Keilausschnitt’ bestimmen (Abbildung (g)). Wie dick ist der Draht in der obenstehenden Abbildung, wenn
der Einschnitt vorne 2mm breit ist?
Aufgabe 12
Die Breite von kleinen Öffnungen kann man mit einem sogenannten ‚Messkeil’ bestimmen
(Abbildung (g)). Bestimme die Breite der Öffnung aus den in der Zeichnung angegebenen
Werten.
4 Winkelfunktionen
Aufgabe 13
Bestimmen Sie in einer Tabelle sin α, cos α und tan α für α = 0◦ , 30◦ , 45◦ , 60◦ , 90◦ , 120◦ , 135◦ ,
1
150◦ , 180◦ , 210◦ , 225◦ , 240◦ , 270◦ sowie für α = 35 π, 74 π, 11
6 π, 2π, 2 6 π.
Aufgabe 14
Vervollständige die Gleichungen zu den untenstehenden Abbildungen. Berechne dann für
Abbildung b) für sin α = 0, 5 und hc = 3 die Länge b. (Fortgeschrittene können schon
p, q, a, c berechnen.)
3
Lösungen
1 A hinreichend für B, A hinreichend für C, B notwendig für A, C notwendig für A,
A⇔B∧C
2 a) falsch b) wahr c) wahr d) falsch
3 Bei der letzten Ziehung der LOTTO-Zahlen war (mindestens) eine Zahl größer als 30.
4 a) 3, 787
b) 25, 714◦ = 25◦ 420 5000
c) 3, 058
8
9
10
11
12
14 a) sin δ =
b) sin α = ac
d
f
cos ε = fd
cos β = aq =
a
c
tan ε = de
tan α =
hc
c
oder tan β =
hc
q
=
b
a
12. Januar 2016, 11:02 Uhr
4
(c)
(d)
(e)
(f)
(g)
5