F20 Reflexions-Anisotropie

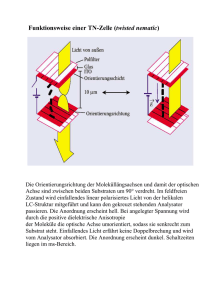
F20 Reflexions-Anisotropie-Spektroskopie
(RAS)
Betreuer: Matthias Wahl
1
Einführung
Reflexions-Anisotropie-Spektroskopie (RAS) ist eine zerstörungsfreie optische Meßmethode, mit der in erster Linie die Oberfläche von Festkörpern
untersucht werden kann. RAS benötigt im Gegensatz zu auf Elektronenbeugung basierenden Techniken wie LEED oder RHEED kein Vakuum und ist
daher relativ problemlos an verschiedenste Wachstums-’Umgebungen’ anpaßbar. Im Gegensatz zur spektroskopischen Ellipsometrie benötigt man im Wesentlichen nur ein einzelnes optisches Fenster, welches senkrechten Lichteinfall auf die Probe ermöglichen muß. Das ermöglicht eine leichte und schnelle
Justage der Apparatur.
RAS wird daher in zunehmendem Maße in der Halbleiterindustrie zur in situKontrolle der einzelnen Wachstumsschritte eingesetzt, d.h. man kann Qualität und Eigenschaften einer auf einem Wafer aufgebrachten Schicht bereits
während des Wachstums kontrollieren und gegebenenfalls gegensteuern bzw.
den Prozeß abbrechen. Im Gegensatz dazu können herkömmliche Untersuchungen nur ex situ, also nach dem Wachsen und Ausschleusen, vorgenommen
werden.
2
Theorie
RAS dient zur Bestimmung anisotroper (d.h. polarisationsabhängiger) Eigenschaften der dielektrischen Funktion von Festkörpern. Wie bei der spektroskopischen Ellipsometrie wird bei der RAS der Polarisationszustand des
von einer Probe reflektierten Lichtes spektral ausgewertet.
Besondere Bedeutung erlangt die RAS bei Untersuchungen an Festkörpern
kubischer Kristallstruktur. Die dielektrischen Eigenschaften des Volumenkristalls (bulk) kubischer Festkörper sind in erster Nährung isotrop (unabhängig
1
Probe
a
b
Ei
Er
Abbildung 1: Entstehung der Polarisationsellipse bei der RAS. Die anisotropen Achsen der Probe sind mit a und b gekennzeichnet.
von der Polarisation des Lichts). Anisotropien entstehen in diesem Fall bevorzugt an der Oberflächen und an Grenzflächen verschiedener Schichten, da
dort die Symmetrie des Volumenkristalls reduziert ist. Das macht die RAS zu
einer oberflächensensitiven Meßmethode. Anisotropien an Oberflächen entstehen beispielsweise
• durch eine u nterschiedliche Anordung der Atome an der Oberfläche im
Vergleich zum Volumen (Rekonstruktion),
• durch anisotrope Filme,
• durch elektronische Zustände an Oberflächen, die unterschiedliche Dispersion im k-Raum entlang der Symmetrieachsen der Oberfläche besitzen.
Abb. 1 zeigt den Effekt einer Reflexions-Anisotropie auf den Polarisationszustand des reflektierten Lichtes. Linear polarisiertes Licht ist nach der Reflexion in der Regel elliptisch polarisiert, wobei die Hauptachsen der Ellipse
um einen kleinen Winkel gegenüber der ursprünglichen Achse verdreht sind.
Dies ergibt sich bei unterschiedlichen komplexen fresnellschen Reflexionskoeffizenten 1 ra , rb in Richtung a und b auf der Probe. Darüber wird das RAS
Signal definiert:
ra − r b
∆r
∆r
∆r
= 1
+ i · Im
(1)
= Re
r
r
r
(r + rb )
2 a
1
Die Fresnel-Koeffizienten verknüpfen die Vektoren der elektrischen Feldstärke des Lichtes vor und nach der Reflexion.
2
0°
PEM
state of
polarization
Analyser
45°
[110]
[001]
−45°
45 °
Sample
0°
Monochromator
Polarizer
Lamp
Abbildung 2: Schematischer Aufbau der RAS-Apparatur. Die anisotropen
Achsen der Probe sind mit Millerschen Indizes gekennzeichnet, bei der Probe
handelt es sich um eine [110]-Oberfläche. Die Funktionsweise der einzelnen
optischen Komponenten wird später beschrieben.
Das RAS Signal ist also eine komplexe Größe und mißt die Reflektivitäten
zweier orthogonal aufeinanderstehender Richtungen (normiert auf die Gesamtreflektivität). Allgemein sind Anisotropien im Vergleich zur Gesamtreliegen im Bereich
flektivität sehr klein. Typische Größen für das Verhältnis ∆r
r
von 10−3 . Der Realteil des RAS-Signals entspricht einer unterschiedlichen Absorption in Richtung a und b, der Imaginärteil entspricht einem Phasenschub
zwischen Richtung a und b. Der Unterschied in der Absorption bewirkt eine
Drehung der Polarisationsachse des Lichtes, während die Phasenverschiebung
für die Elliptizität des Lichts verantwortlich ist.
3
Meßaufbau und optische Komponenten
Abb. 2 zeigt den prinzipiellen Aufbau der RAS-Apparatur. Das Licht einer
75W Xe-Hochdrucklampe wird über einen Hohlspiegel auf die Probe fokussiert. Das Licht sollte möglichst senkrecht auf die Probe treffen. Beim Durchlaufen des Polarisatorprismas wird das Licht senkrecht zur Einfallsebene linear polarisiert. Das reflektierte Licht durchläuft die Analysatoreinheit, be-
3
Photomultiplier (CaF2 −Fenster)
Vorverstärker
Monochromator (UV)
Xenon−Hochdrucklampe
Detektoren (Si und InGaAs)
Halogenlampe
Polarisator
(MgF2 )
zur Probe
Monochromator (IR)
Monochromator−Wechsler
Photoelastischer
Modulator(PEM)
(CaF2 )
Analysator
(MgF2 )
Abbildung 3: Photo einer RAS-Apparatur des Institutes. Um den spektralen
Bereich zu erweitern, werden zwei Monochromatoren und drei Detektoren
(Photomultiplier, Si- und InGaAs-Diode) verwendet. Mittels eines fahrbaren
Spiegels kann zwischen den beiden Monochromatoren gewechselt werden. Der
spektrale Bereich umfaßt die Energien von 0.75 eV bis 6.5 eV.
stehend aus photoelastischem Modulator (PEM) und Analysatorprisma. Die
optische Achse des PEM steht dabei ebenfalls senkrecht zur Einfallsebene des
Lichts, der Analysator im 45◦ -Winkel dazu. Das modulierte und analysierte
Licht wird über weitere Spiegel in den Eintrittsspalt des Monochromators
fokussiert und detektiert. Abb. 3 zeigt ein Photo einer RAS-Apparatur.
Das detektierte Signal besteht aus einem (sehr kleinen) modulierten Anteil
(AC) und einer überlagerten Gleichspannung (DC). Mittels eines Lock-InVerstärkers wird der modulierte Anteil in eine zu AC proportionale Gleichspannung umgewandelt. Diese ist proportional zu ∆r (siehe Gleichung 1).
Der Gleichspannungsanteil wird über eine AD-Wandlerkarte aufgezeichnet
und entspricht der Gesamtreflektivität r = 21 (ra + rb ). Das Meßprogramm
berechnet aus diesen Größen das RAS-Signal.
Im Folgenden soll auf die einzelnen optischen Komponenten genauer eingegangen werden und die Signalentstehung diskutiert werden.
4
Polarisator
ordentlich
ausserordentlich
Analysator
ausserordentlich
ordentlich
Abbildung 4: Wirkungsweise der Rochonprismen als Polarisator und Analysator. Beim Polarisator ist das Licht nach dem Austritt vollständig linear
polarisiert. Beim Analysator wird das Polarisationsverhältnis in ein Intensitätsverhältnis transformiert. Die Ausrichtung der optischen Achse ist in
den Ecken der Teilprismen angedeutet.
3.1
Polarisatorprismen
Die verwendeten Polarisationsprismen sind zumeist Rochon-Prismen, so daß
diese im Folgenden etwas näher beschrieben werden (siehe dazu Abb. 4).
Rochonpolarisatoren bestehen aus zwei Teilprismen, deren optische Achsen
senkrecht aufeinander stehen, wobei eine der Achsen in Ausbreitungsrichtung
des Lichts orientiert ist. Durch Doppelbrechung an der Grenzfläche der Teilprismen entstehen am Prismenausgang zwei Strahlenbündel: der ordentliche
(o für ordinary) und der außerordentliche (e für extraordinary) Strahl. Der
elektrische Feldvektor des ordentlichen Strahls schwingt senkrecht zur den
optischen Achsen beider Teilprismen.
Der Brechungswinkel φ am Übergang der beiden Teilprismen läßt sich mit
Hilfe des Brechungsgesetzes berechnen:
sin φ =
no
cos S
ne
(Polarisator)
5
(2)
beziehungsweise
ne
cos S
(Analysator)
(3)
no
wobei S der Schnittwinkel der Schräge ist. Der außerordentliche Strahl ist
immer farblich aufgespalten, da ne (wie auch no ) abhängig von der Wellenlänge ist (Dispersion) – dies bedeutet unterschiedliche Brechungswinkel
für den außerordentlichen Strahl beim Austritt aus dem rechten Teilprisma.
Der ordentliche Strahl geht immer senkrecht durch das Prisma und wird nie
gebrochen.
Je nach Wellenlängenbereich müssen unterschiedliche Materialien verwendet
werden. In den RAS-Apparaturen im Institut bestehen die Rochonprismen
zumeist aus kristallinem Quarz oder Magnesiumfluorid (MgF2 , transparent
vom Infraroten bis ins UV). Eine Auswahl an Materialien zeigt Abb. 5.
sin φ =
3.1.1
Das Rochon-Prisma als Polarisator
Die vertikalen (|) und horizontalen (•) Anteile treten in die linke Hälfte des
Prismas ein (siehe dazu Abb. 4 oben). Der Brechungsindex ist für beide Polarisationsanteile derselbe, da die optische Achse senkrecht zu den beiden
Polarisationsrichtungen gerichtet ist.
Aufgrund der optischen Aktivität des Kristalls (Ausbreitungsrichtung entlang der optischen Achse) kommt es jedoch zu einer Drehung der Polarisationsanteile (Drehung stark wellenlängenabhängig). Die an der Grenzfläche
der beiden Prismenhälften ankommende Polarisation hat nichts mehr mit der
ursprünglich durch die Stirnfläche getretenen gemein.2 Trifft nun ein solches
Gemisch von Polarisationsanteilen auf die Grenzfläche, so sehen“die vertika”
len Anteile keinerlei Änderung im Brechungsindex (n = no ). Die horizontalen
Anteile hingegen bewegen sich in der rechten Prismenhälfte mit nm re > nm ro
(im Falle von optisch positiven Kristallen wie Quarz oder MgF2 ), so daß der
Strahl zum Lot hin gebrochen wird (Übergang in ein optisch dichteres Medium).
3.1.2
Das Rochon-Prisma als Analysator
In diesem Fall (siehe Abb. 4 unten) kommt es schon bei Eintritt des Lichts
in die linke Hälfte zu einer Phasenverschiebung zwischen beiden Polarisationsanteilen. Da der Eintritt aber senkrecht verläuft, kommt es nicht zu einer
2
An dieser Stelle wird auch klar, warum man ein Rochonprisma in dieser Konfiguration nicht als Analysator betreiben kann - man bekommt bei Einstrahlung von linear
polarisiertem Licht keine Auslöschung.
6
Abbildung 5: Brechungsindizes zweier uniaxialer, doppelbrechender Kristalle:
kristalliner Quarz (α-Quarz) und Magnesiumfluorid. Der außerordentliche
Brechungsindex ist mit ne , der ordentliche mit no bezeichnet. Beides sind im
dargestellten Spektralbereich optisch positive Kristalle (ne > no ). MgF2 ist
in einem größeren spektralen Bereich doppelbrechend.
7
Spannungs− und
Doppelbrechungseigenachsen
zum Oszillator−Steuerteil
Strahlengang
Piezoquartz
spannungsdoppelbrechender
Kristall
Abbildung 6: Aufbau des PEM der Firma HINDS. Die Spannungsdoppelbrechung wird in diesem Fall durch eine einzige Piezokeramik erzeugt. Die
Spannung bzw. Dehnung wird longitudinal im Kristall aufgebaut.
räumlichen Aufspaltung beider Teilstrahlen. Dies geschieht erst an der Grenzfläche der beiden Teilprismen, wo der vertikale Anteil keinen Unterschied im
Brechungsindex sieht, der horizontale jedoch vom Lot weggebrochen wird
(Übergang zum optisch dünneren Medium).
In der rechten Hälfte des Prismas kommt nun wieder die optische Aktivität
des Kristalls ins Spiel. Sie bewirkt wieder eine Drehung für die zum ordentlichen Strahl parallelen Anteile, so daß sowohl im ordentlichen als auch im
außerordentlichen Strahl beide Polarisationsanteile enthalten sind. Ihre Intensität ist aber proportional zu den ins Rochonprisma eingetretenen Polarisationsanteilen, so daß man hier eine Auslöschung erhalten kann.3 Die
Polarisation des austretenden Lichts entspricht eben nur nicht der des eingetretenen.
Benutzt man einen polarisationsunabhängigen Detektor hinter dem Prisma,
kann das Rochonprisma also als Analysator verwendet werden.
3.2
Photoelastischer Modulator (PEM)
Der PEM besteht aus spannungsdoppelbrechendem Quarzglas oder Kalziumfluorid, das periodisch mit der Frequenz ωPEM (meistens 50 kHz) durch
eine Piezokeramik unter mechanische Spannung gesetzt wird. (siehe Abb.
6). Dadurch ergibt sich ein sich periodisch ändernder Laufzeitunterschied4
δ = δ0 sin(ωPEM t) zwischen Licht polarisiert entlang der Achse des PEM
3
Auslöschung des ordentlichen Strahls bei horizontaler Polarisation, Auslöschung des
außerordentlichen Strahls bei vertikaler Polarisation.
4
wird auch als Retardierung bezeichnet
8
und senkrecht dazu (siehe Abb. 7). Die Größe des Laufzeitunterschiedes wird
durch die Wellenlänge und Stärke der mechanischen Spannung bestimmt und
kann variiert werden.
Abb. 8 zeigt den Polarisationszustand innerhalb einer Schwingungsperiode des PEM. Wird ein RAS-Spektrum aufgenommen, muß für jede Wellenlänge die Retardierung neu eingestellt werden, damit bei jeder Wellenlänge
gleich retardiert wird. Das liegt im Wesentlichen an den unterschiedlichen
optischen Weglängen innerhalb des Kristalls. Das Meßprogramm macht dies
automatisch. Von Zeit zu Zeit jedoch muß der PEM in dieser Hinsicht neu
kalibriert werden.
3.3
Signalentstehung
Wie weiter oben erwähnt ist das RAS-Signal eine komplexe Größe. Mit Hilfe von PEM und nachgestelltem Analysator können sowohl der Realteil als
auch Imaginärteil getrennt detektiert werden. Der Realteil des RAS-Signals
wird vom PEM mit 2ωPEM moduliert, während der Imaginärteil mit einfacher PEM-Frequenz moduliert wird. Wie das Signal in doppelter Frequenz
entsteht, wird in Abb. 9 für eine Retardierung von δ0 = λ2 anschaulich verdeutlicht. Abb. 10 verdeutlicht die Entstehung des imaginären RAS-Signals
am Detektor bei kleinem Phasenschub zwischen den Richtungen a und b auf
der Probe (es entsteht also elliptisch polarisiertes Licht). Hier ist die Retardierung des PEM auf λ4 gesetzt, bei der die einfache Frequenzkomponente
ungefähr ihr Maximum erreicht.
Nach Reflexion an der Probe ist das Licht durch unterschiedliche Absorption in Richtung a und b auf der Probe leicht unterschiedlich polarisiert. Im
Falle des Realteils entstehen Maxima in der Intensität zum Zeitpunkt maximaler Spannung und Dehnung. Das Detektorsignal besteht dann aus einer
Gleichspannung (DC), welche proportional zur Gesamtreflektivität ist und
einem mit doppelter PEM-Frequenz moduliertem Anteil (AC), der mittels
des Lock-In ausgewertet wird. Im Falle des Imaginärteils entstehen Maxima/Minima zum Zeitpunkt maximaler Spannung/Dehnung. Der AC Anteil
des Signals ist also mit einfacher PEM Frequenz moduliert.
In der Realität enthalten Real- und Imaginärteil aufgrund der sinusförmigen
Modulation des PEM weitere Frequenzanteile, und zwar im Falle des Realteils
die 2-,4-,6-,...fache PEM-Frequenz und die 1-,3-,5-,...fache PEM Frequenz im
Falle des Imaginärteils. Die normierte AC-Anteil der Intensität am Detektor
9
Keine Spannung:
PEM−Achsen
E
Ey
45°
Ex
PEM
x und y Komponente
in Phase
Spannung durch Kompression:
E
Ey
45°
Ex
x Komponente eilt y Komponente
voraus
Spannung durch Dehnung:
E
Ey
45°
Ex
y Komponente eilt x Komponente
voraus
Abbildung 7: Arbeitsweise des PEM für linear polarisiertes Licht. Das einfallende Licht ist in diesem Fall 45◦ zu den Modulatorachsen polarisiert. Bei
Doppelbrechung (durch Kompression und Dehnung) entsteht ein Laufzeitunterschied zwischen den beiden Vektorkomponenten parallel zu den Achsen.
10
λ
2
Zeit
λ
2
Polarisationszustand
linear
rechts
zirkular
linear
rechts
zirkular
linear
links
zirkular
linear
links
zirkular
linear
Abbildung 8: Arbeitsweise des PEM für linear polarisiertes Licht bei einer
Retardierung von δ0 = λ2 . Es ist eine Schwingungsperiode gezeigt. Der Polarisationszustand wechselt mit doppelter PEM-Frequenz zwischen linear und
zirkular polarisiert.
läßt sich näherungsweise folgendermaßen ausdrücken:
∆r
∆I
= −2 Im
J1 (δPEM ) sin ωPEM t
I
r
∆r
J2 (δPEM ) cos 2ωPEM t + . . . ,
+ 2 Re
r
(4)
wobei hier J1 und J2 die Besselfunktionen erster bzw. zweiter Ordung sind.
Diese Vorfaktoren sind abhängig von der Retardierung δPEM des PEM. Das
RAS-Signal ist also proportional zum gemessenen Intensitätsverhältnis ∆I
.
I
Die einfache bzw. doppelte PEM-Frequenz wird dann als Referenz für den
nachgeschalteten Lock-In verwendet, um den Imaginär bzw. Realteil getrennt
aufzunehmen. Manche Apparaturen haben auch zwei Lock-In-Verstärker, um
Real- und Imaginärteil simultan aufzunehmen. In diesem Fall wird die Retardierung zwischen λ4 und λ2 gewählt.
3.4
Systematische Fehler
Systematische Fehler entstehen durch Bauteileigenschaften oder Dejustage
optischer Elemente im Strahlengang. Man kann folgende im Vergleich zu (4)
11
ursprünglicher Polarisationszustand:
Polarisation nach Reflexion:
PEM Achse
Kristallachse a
Kristallachse b
45°
PEM Achse
Analysator Achse
Polarisation nach Durchlaufen des PEM:
PEM Achse
Detektorspannung
PEM Achse
AC
Analysator Achse
Retardierung um
λ /2
DC = Mittelwert
keine Retardierung
Zeit
PEM Periode
Abbildung 9: Schematische Entstehung des RAS Realteil-Signals bei einer
Retardierung von λ2 . Eigentlich erhält das Signal weitere Frequenzkomponenten, hier sind nur Frequenzen in doppelter Modulatorfrequenz gezeigt. Die
Projektionen des modulierten Lichts auf die Analysatorachse lassen Maxima
beim retardiertem und Minima beim nicht retardiertem Polarisationszustand
erkennen. Unten rechts ist das Signal des Detektors skizziert. Es besteht aus
einem Offset (DC) und dem modulierten Anteil (AC). Der Effekt ist in diesem
Bild stark übertrieben gezeichnet.
12
ursprünglicher Polarisationszustand:
Polarisation nach Reflexion:
PEM Achse
Kristallachse a
Kristallachse b
45°
PEM Achse
Analysator Achse
Polarisation nach Durchlaufen des PEM:
PEM Achse
Detektorspannung
PEM Achse
AC
Analysator Achse
Retardierung um
λ /4
DC
Retardierung um
−λ /4
Zeit
PEM Periode
Abbildung 10: Entstehung des RAS Imaginärteil-Signals in einfacher
PEM-Frequenz bei einer Retardierung von λ4 . Innerhalb einer PEMSchwingungsperiode entstehen Maxima und Minima bei maximaler Stauchung bzw. Dehnung des Kristalls. Auch hier enthält das RAS-Signal weitere
Frequenzkomponenten, die hier nicht gezeigt sind. Der Effekt ist stark übertrieben dargestellt.
13
erweiterte Formel für die relative Gesamtintensität angeben (höhere Ordnungen weggelassen):
∆I
∆r
= 2 −Im
+ δ1 cos 2Θ1 + δ2 cos 2Θ2 − 2αp J1 (δPEM ) sin ωPEM t
I
r
∆r
+ 2 Re
+ 2∆M + 2∆P J2 (δPEM ) cos 2ωPEM t + . . .
r
(5)
Hierbei bezeichnet ∆P bzw. ∆M eine Fehlstellung des Polarisators bzw.
PEM, αp ist der durch einen nichtidealen Polarisator verursachte Restanteil
zirkularer Polarisation. Diese Fehlerquellen können durch Messung an isotropen Proben eliminiert werden.
Bei Messungen von Proben in der Gasphasenepitaxie (MOVPE) oder im Ultrahochvakuum (UHV) muß ein Fenster zur Wachstumskammer durchlaufen
werden. Diese Fenster zeigen aufgrund ihrer Einspannung immer eine mehr
oder weniger starke Spannungsdoppelbrechung auf, so daß eine Phasendifferenz δ1 und δ2 zwischen Licht der ’langsamen’ und ’schnellen’ Achse entsteht.
Der Azimutwinkel dieser Achsen zur Einfallsebene ist Θ1 und Θ2 . Diese Beiträge sind von Fenster zu Fenster sehr unterschiedlich (sie hängen auch vom
durchstrahlten Bereich des Fensters ab) und können nur durch Drehung der
Probe um 90◦ eliminiert werden, was leider oftmals im UHV nicht möglich
ist.
4
Versuchsablauf und Auswertung
Der Ablauf der Experimente hängt stark von der benutzten RAS-Apparatur
und der gerade zur Verfügung stehenden Epitaxieanlage ab. Genaueres wird
in der Vorsprache erklärt.
5
Kontrollfragen
Diese Kontrollfragen sollen helfen, das Gelesene kritisch zu reflektieren.
1. Wie entsteht aus linear polarisiertem Licht durch Reflexion elliptisch
polarisiertes Licht?
2. Wie sehen die Fresnell-Formeln aus und welche Bedeutung hat der senkrechte Lichteinfall?
3. Wozu benötigt man den Lock-In-Verstärker?
14
4. Nach welchem Prinzip funktionieren Polarisationsprismen (speziell der
Rochon-Polarisator)?
5. Wie werden Real- und Imaginärteil des RAS-Signals getrennt?
6. Wie verhält sich das Signal am Detektor, wenn der PEM ausgeschaltet
ist (keine Retardierung)?
7. Wie ändert sich das RAS-Signal, wenn die Probe um 180◦ gedreht wird?
8. Was passiert mit dem RAS-Signal, wenn die Probe um 90◦ gedreht
wird?
9. Welche Änderung des Signals ist zu erwarten, wenn sich die Intensität
der Lichtquelle ändert?
10. Welche Bedeutung haben die Besselfunktionen?
11. Warum (und wie) hängt die Retardierung des PEM von der Wellenlänge
ab?
6
Weitere Literatur für Interessierte
In der Arbeitsgruppe Richter existieren diverse Diplomarbeiten und Laborpraktikumsberichte über RAS und polarisationsabhängige Reflexionsmessungen im Allgemeinen, die auch zum Teil als Quelle dieses Skriptes dienten.
Genannt seien hier nur einige (in chronologischer Reihenfolge):
Literatur
[1] Stefan Scholz: Polarisationsmodulierte Reflexion an Halbleiteroberflächen, Diplomarbeit 1992
[2] Jens Rumberg: RAS und andere Kleinigkeiten, Laborpraktikumsbericht
1993
[3] Knut Stahrenberg: Messen mit der RAS, Laborpraktikumsbericht 1994
[4] Jens Rumberg: RAS für Doofe, 1994
Bei Interesse fragen sie bitte den Betreuer ihres Vertrauens.
15