1 AVL-Bäume

1 AVL-Bäume
1.1 Aufgabentyp
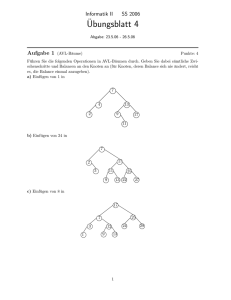
Fügen Sie in einen anfangs leeren AVL–Baum die folgenden Schlüssel ein:
...
Wenden Sie hierbei konsequent den Einfüge–/Balancierungsalgorithmus an und dokumentieren Sie die ausgeführten Operationen.
Nutzen Sie die Abkürzungen:
i(x) - für das Einfügen des Knotens mit dem Schlüsselwert x,
L(x) - für die Linksrotation um den Knoten mit dem Schlüsselwert x,
R(x) - für die Rechtsrotation um den Knoten mit dem Schlüsselwert x.
1.2 Überblick
1. i(x): neues Element als Blatt einfügen, sodass Suchbaumeigenschaft erfüllt bleibt
2. Balancewerte auf Einfügepfad Richtung Wurzel berechnen (bn =maximale Pfadlänge
rechts - maximale Pfadlänge links), solange bn ∈ {1, 0, −1} bzw. Wurzel erreicht
3. Falls bn = −2 oder bn = 2, wähle eine Variante:
bn = −2 bn−1 = 1:
Doppelrotation: L(n − 1), R(n)
bn = 2
bn−1 = −1: Doppelrotation: R(n − 1), L(n)
bn = −2 bn−1 = −1: Einfachrotation: R(n)
bn = 2
bn−1 = 1:
Einfachrotation: L(n)
4. Bei Rotation abgetrennte Nachfolger wieder normal“ in Suchbaum einfügen
”
1.3 Grundidee
Ein naiver Algorithmus zum Suchen besteht darin, einfach alle Elemente aus der Datenmenge mit dem zu suchenden Element zu vergleichen. Dies ist natürlich sehr ineffizent.
Besser ist es, wenn die Daten schon sortiert sind. Da dies jedoch relativ aufwändig ist,
bieten Suchbäume einen guten Mittelweg an. Für jeden Knoten eines Suchbaums gilt: alle
Schlüssel im linken Teilbaum sind kleiner und alle Schlüssel im rechten Teilbaum sind
größer als der Schlüssel des Knotens. Somit ist es also möglich in O(log n) statt O(n)
Schritten die Suche abzuschließen. Normale Suchbäume haben allerdings das Problem,
dass sie sehr schnell entarten können. Wird ein solcher Suchbaum aus einer schon aufsteigend sortierten Liste erstellt, entsteht als Baum“ wiederum nur eine Liste (bzw. alle
”
Knoten des Baumes haben keinen linken Nachfolger). Damit hat der Baum gegenüber
der Liste keine Verbesserung gebracht. Balancierte Bäume sollen dieses Problem beheben,
indem bei jeder Einfüge/Lösche-Operation darauf geachtet wird, dass der Baum nicht
entartet“, also die Anzahl der linken bzw. rechten Nachfolger jedes Knotens in etwas
”
gleich ist.
Die AVL-Bäume, benannt nach Adelson-Velskij und Landis, sind solche balancierten Bäume,
1
bei denen sich die Höhen des linken und rechten Teilbaums um höchstens 1 unterscheiden.
Die in der Übung behandelten Operationen beziehen sich ausschließlich auf das Einfügen
von Elementen in einen AVL-Baum. Die Schrittfolge hierbei ist recht einfach: Zuerst wird
der Wert so eingefügt, dass die Suchbaumeigenschaft erhalten bleibt, danach wird geprüft,
ob die AVL-Eigenschaft noch gilt (also ob der Baum ausbalanciert ist). Wenn dies nicht
der Fall ist, wird durch Rotationen eine Balance geschaffen.
1.4 Erklärung am Beispiel
In einen anfangs leeren AVL–Baum sollen folgende Zahlen eingefügt werden: 8, 4, 2, 0, 1,
3, 5, 9, 6, 7, 10.
Zuerst soll die 8 (in den noch leeren) Baum eingefügt werden. Die Suchbaumeigenschaft
ist offenbar immer erfüllt, wenn der Baum nur aus einem Wurzelknoten besteht. Also wird
der neue Baum nur aus der 8 als Wurzel bestehen. Als nächstes ist zu prüfen, ob der Baum
auch noch die AVL-Eigenschaft erfüllt. Dafür muss für jeden Knoten auf dem Einfügepfad
die Balance berechnet werden. Der Einfügepfad besteht hier offenbar nur aus dem Knoten
mit der 8 selber. Dieser ist jedoch ein Blatt und hat somit die Balance 0 (rechter-linker
Nachfolger=0-0=0). Damit ergibt sich:
80
i(8)
−→
Als nächstes soll die 4 eingefügt werden. 4 ist offenbar kleiner als 8, muss also im linken
Teilbaum der 8 zu finden sein (Suchbaumeigenschaft). Da die 8 noch keine Nachfolger hat,
wird die 4 selber der direkte linke Nachfolgerknoten der 8. Nun muss auf dem Einfügepfad
(8,4) in Richtung Wurzel (4,8) die Balance berechnet werden. Der Knoten 4 ist ein Blatt
hat also die Balance 0. Die 8 hat keinen rechten Nachfolger, aber einen linken Nachfolger,
also ergibt sich als Balance 0-1=-1:
8−1
i(4)
−→
40
Nun wird die 2 hinzugefügt: 2 ist kleiner als 8, also in den linken Teilbaum. 2 ist kleiner als
4, also in den linken Teilbaum der 4. Da dieser nicht existiert, wird dort die 2 angehängt:
8−2
i(2)
−→
4−1
20
Die Berechnung der Balance (Reihenfolge: 2,4,8) ergibt einen Widerspruch der AVLEigenschaft an der 8 (Da der Balancewert nicht -1,0 oder 1 ist). Da der letzte“ und
”
vorletzte“ betrachtete Balancewert jeweils negativ ist, erfolgt eine einfache Rotation. Of”
fenbar ist der Baum stark linkslastig“, sodass nach rechts (d.h. im Uhrzeigersinn) gedreht
”
werden muss. Die Rotationsachse“ ist bei einer Einfachrotation der Knoten, bei dem der
”
AVL-Fehler zuerst aufgetreten ist, hier also die 8:
2
40
R(8)
−→
20
80
Nun wird die 0 hinzugefügt. Da 0 kleiner als 4 und kleiner als 2 ist, wird sie links an
die 2 gehängt. Die Balancewerte werden nun in der Reihenfolge 0,2,4 berechnet und die
AVL-Eigenschaft bleibt erhalten:
4−1
i(0)
−→
2−1
8
00
Da die 1 kleiner 4, kleiner 2 aber größer als 0 ist, wird sie rechts an die 0 angehängt.
Die Berechnung der Balancewerte erfolgt wieder entlang des Einfügepfades in Richtung
Wurzel, wobei bei der 2 schon ein Fehler“ auftritt. An dieser Stelle kann die Berechnung
”
abgebrochen werden, da bereits klar ist, welche Rotation erfolgen muss:
4
i(1)
−→
2−2
8
01
10
Offenbar hat ein Vorzeichenwechsel bei den Balancewerten (-2 und 1) stattgefunden, sodass
eine Doppelrotation ausgeführt werden muss. Eine Doppelrotation beginnt bei dem vor”
letzten“ betrachteten Element (bezüglich der Balancewerte) mit einer Rotation. Danach
wird auf das letzte“ Element die genau gegenläufige Rotation ausgeführt. Das vorletzte“
”
”
Element ist hier offenbar die 0. Der der Teilbaum der 0 rechtslastig“ ist, erfolgt zuerst
”
eine Linksrotation um die 0, danach eine Rechtsrotation um die 2:
4
4
L(0)
−→
2
1
8
R(2)
−→
1
0
8
2
0
Balancewerte müssen hier nicht (zwangsläufig) neu berechnet werden, da eine korrekte
Rotation die AVL-Eigenschaft erzwingt. Zur Überprüfung ist dies jedoch trotzdem empfehlenswert.
Jetzt wird die 3 hinzugefügt. Da 3 kleiner 4, aber 3 größer als 1 und 2 wird diese als
rechter Nachfolger an die 2 angehängt. Die Berechnung der Balancewerte ergibt wieder
einen Fehler, da die 4 den Wert -2 hat:
3
4−2
i(3)
−→
11
8
21
0
30
Offenbar hat auch hier ein Vorzeichenwechsel stattgefunden, sodass es sich um eine Doppelrotation handeln muss. Der vorletzte“ Teilbaum (Knoten 1) ist wieder stark rechtslastig,
”
sodass zuerst eine Linksrotation um die 1 ausgeführt werden muss und dann eine Rechtsrotation um die 4. Bei letzterer ergibt sich das Problem, dass der Baumknoten 3 abgespalten
wird. Dieser muss nach der Rotation unter der Beachtung der Suchbaumeigenschaft wieder
hinzugefügt werden (3 größer 2, aber 3 kleiner 4, also als linker Nachfolger der 4):
2
4
2
L(1)
−→
1
8
1
R(4)
−→
3
0
4
3
8
0
Das Hinzufügen der 5 und 9 erfolgt nun ohne, dass eine Rotation nötig wird:
21
41
1
i(5)
−→
0
3
8−1
50
21
41
1
i(9)
−→
0
80
3
5
90
Das Einfügen der 6 hat wiederum eine zu schlechte Balance zur Folge. Durch die verschiedenen Vorzeichen (2 und -1), ist eine Doppelrotation nötig. Da der Teilbaum mit Knoten
8 linkslastig ist, erfolgt zuerst eine Rechtsrotation um die 8. Danach eine Linksrotation
um die 4:
4
2
2
42
1
i(6)
−→
0
3
1
R(8)
−→
8−1
0
51
2
4
3
5
9
0
8
60
1
L(4)
−→
5
4
3
8
6
9
9
6
Nach dem Einfügen der 7 liegt ein einfacher“ Fehler vor, da kein Vorzeichenwechsel statt”
gefunden hat (die letzten Balancewerte sind 2 und 1). Offenbar ist der Baum mit Wurzelknoten 2 rechtslastig, also muss eine Linksrotation um die 2 erfolgen. Dabei wird jedoch
der Baum mit dem Wurzelknoten 4 abgespalten“, sodass dieser nach erfolgter Rotation
”
wieder angefügt werden muss (unter Einhaltung der Suchbaumeigenschaft, also als rechter
Nachfolger der 2):
22
51
1
i(7)
−→
0
5
4
8−1
61
3
2
L(2)
−→
1
9
0
8
4
3
6
9
7
70
Das Einfügen der 10 ändert nichts an der vorhandenen AVL-Eigenschaft, sodass keine
Rotation nötig ist:
50
80
2
i(10)
−→
1
0
4
91
6
3
7
100
1.4.1 Eigenschaften
Komplexität: O(log n) (für Suchen, Einfügen und Löschen)
5