Ubungsblatt 4 - AG CGVR Uni

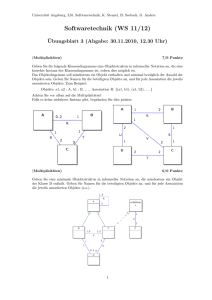
Informatik II
SS 2006
Übungsblatt 4
Abgabe: 23.5.06 - 26.5.06
Aufgabe 1
(AVL-Bäume)
Punkte: 4
Führen Sie die folgenden Operationen in AVL-Bäumen durch. Geben Sie dabei sämtliche Zwischenschritte und Balancen an den Knoten an (für Knoten, deren Balance sich nie ändert, reicht
es, die Balance einmal anzugeben).
a) Einfügen von 1 in
PSfrag replacements
7
4
13
2
9
17
11
PSfrag replacements
b) Einfügen von 24 in
7
17
2
11
3
25
13 22
9
PSfrag replacements
27
c) Einfügen von 8 in
17
25
7
3
1
24
12
9
13
1
29
PSfrag replacements
d) Einfügen von 16 in
11
20
6
4
12
Aufgabe 2
24
15
8
17 23
(B-Bäume)
Punkte: 3+1+1
a) Fügen Sie in einen zu Begin leeren B-Baum der Klasse τ (1, h), h ≥ 0 die folgenden Elemente
ein: 9, 23, 15, 17, 90, 4, 40, 36, 75, 25, 54, 1.
b) Löschen Sie in dem folgenden B-Baum der Klasse τ (1, 4) nacheinander die Elemente 14 und
45.
PSfrag replacements
29
13
46
9
2
18
10
14
44
25
35
71
45
60
87
PSfrag replacements
c) Führen Sie für den folgenden B-Baum der Klasse τ (2, h), h ≥ 0 nacheinander die Operationen
“Einfügen von 25” und “Löschen von 11” aus.
12
8
Aufgabe 3
11
15
16
18
31
17
19
(AVL-Bäume in Python)
20 21
24
33 34
Punkte: 8
Laden Sie die Datei avl tree incomplete.tar.gz von der Homepage und entpacken Sie diese. Sie finden in der entpackten Datei 2 Klassen(Node und AVLTree). Letztere ist unvollständig. Ergänzen
Sie überall, wo “TODO” steht, den Code. An einigen Stellen stehen Fragezeichen(?) welche auch
ersetzt werden müssen.
Überlegen Sie sich zunächst wie das rekursive Einfügen eines Elementes in einen Baum funktioniert und wie die Balancen korrigiert werden müssen. Wie ändert sich die Balance an den
Knoten, an dem das neue Element als Kindknoten angehängt wird? Wann ändert sich die Balance auch am Vaterknoten, an dessen Vaterknoten usw.?
Überlegen Sie sich sinnvolle Testbeispiele(Folge von Elementen) und ergänzen Sie den Testcode
um diese.
2
Aufgabe 4
(Kurzfragen)
Punkte: 1,5
Definition: Ein Baum heisst vollständig ausgeglichen gdw
• für alle Knoten unterscheidet sich die Anzahl der Knoten in den Teilbäumen höchstens um
1
• alle Blätter des Baumes unterscheiden sich in ihrem Abstand zur Wurzel um höchstens 1
a) Gibt es AVL-Bäume, die nicht vollständig ausgeglichen sind?
b) Gibt es vollständig ausgeglichene Bäume, die keine AVL-Bäume sind?
c) Wieviele Ausgleichsoperationen sind maximal notwendig, um einen Baum, der vor einer
Einfügeoperation die AVL-Eigenschaft besitzt, nach dieser Operation wieder in einen AVL-Baum
zu überführen?
3