trigonometrische Funktionen x tan x arctan x cot x arccot x arcsec x

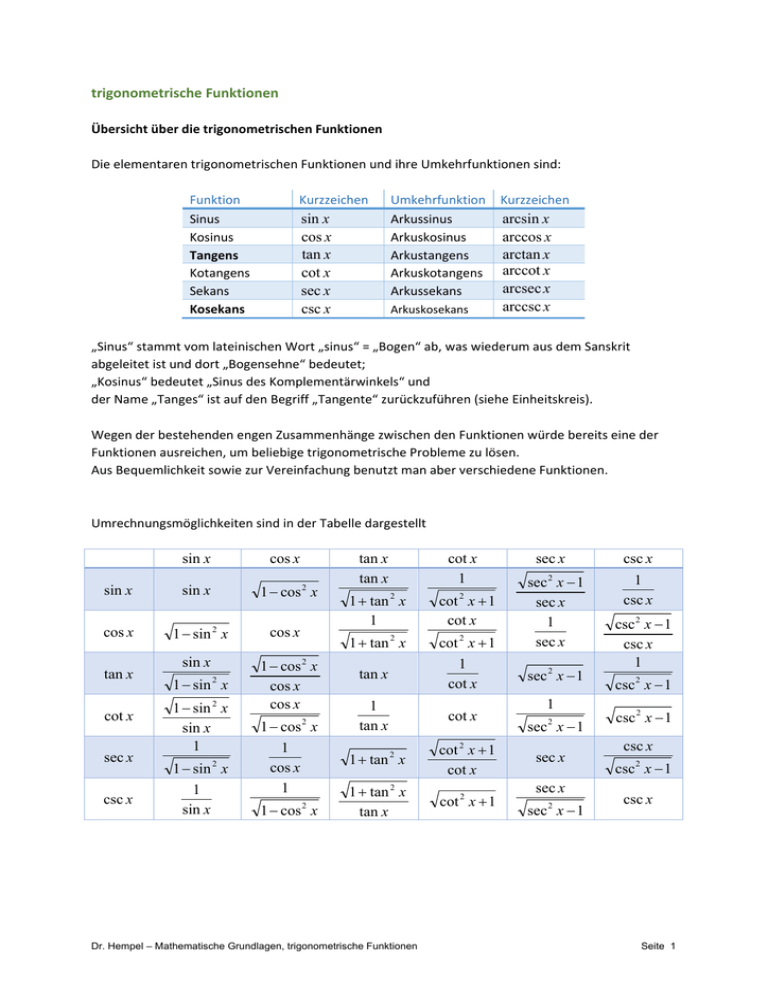
trigonometrische Funktionen Übersicht über die trigonometrischen Funktionen Die elementaren trigonometrischen Funktionen und ihre Umkehrfunktionen sind: Funktion Kurzzeichen Umkehrfunktion Kurzzeichen sin x arcsin x Sinus Arkussinus cos x arccos x Kosinus Arkuskosinus tan x arctan x Tangens Arkustangens Kotangens cot x Arkuskotangens arccot x arcsec x sec x Sekans Arkussekans arccsc x csc x Kosekans Arkuskosekans
„Sinus“ stammt vom lateinischen Wort „sinus“ = „Bogen“ ab, was wiederum aus dem Sanskrit abgeleitet ist und dort „Bogensehne“ bedeutet; „Kosinus“ bedeutet „Sinus des Komplementärwinkels“ und der Name „Tanges“ ist auf den Begriff „Tangente“ zurückzuführen (siehe Einheitskreis). Wegen der bestehenden engen Zusammenhänge zwischen den Funktionen würde bereits eine der Funktionen ausreichen, um beliebige trigonometrische Probleme zu lösen. Aus Bequemlichkeit sowie zur Vereinfachung benutzt man aber verschiedene Funktionen. Umrechnungsmöglichkeiten sind in der Tabelle dargestellt sin x cos x tan x cot x sec x csc x sin x sin x cos x 2
tan x cot x sec x csc x 1 sin x sin x
1  sin x
2
1  sin 2 x
sin x
1
1  sin x
1
sin x
2
1 cos 2 x cos x 1  cos 2 x
cos x
cos x
1  cos x
1
cos x
1
2
1  cos 2 x
tan x
1
1  tan x
1
cot x  1
cot x
1  tan 2 x
cot 2 x  1
1
cot x
2
tan x 2
1
tan x
cot x 1 tan 2 x cot 2 x  1
cot x
1  tan 2 x
tan x
cot 2 x  1 sec 2 x  1
sec x
1
sec x
sec 2 x  1 1
sec 2 x  1
sec 2 x  1
csc 2 x  1
csc x
1
csc 2 x  1
csc 2 x  1 csc x
sec x sec x
1
csc x
csc 2 x  1
csc x Dr. Hempel – Mathematische Grundlagen, trigonometrische Funktionen
Seite 1
Die trigonometrischen Funktionen lassen sich bezüglich Größe und Vorzeichen recht gut am Einheitskreis darstellen:  für beliebige Winkel ist der Sinus am Einheitskreis als Quotient aus Gegenkathete und Hypotenuse definiert; bei einer Hypotenuse der Länge 1 (Einheitskreis!) entspricht das der y‐Koordinate des Schnittpunktes am Einheitskreis. 
für beliebige Winkel ist der Kosinus am Einheitskreis als Quotient aus Ankathete und Hypotenuse definiert; bei einer Hypotenuse der Länge 1 (Einheitskreis!) entspricht das der x‐Koordinate eines Punktes am Einheitskreis. Dr. Hempel – Mathematische Grundlagen, trigonometrische Funktionen
Seite 2

der Tangens entspricht dem Quotienten aus Sinus und Kosinus; er ist damit das Längenverhältnis der Gegenkathete zur Ankathete; bei einer Ankathete der Länge 1 (Einheitskreis!) entspricht das der y‐Koordinate des Schnittpunktes des Schenkels unseres Winkels mit der senkrechten Tangente am Einheitskreis: 
reziprok zum Tangens entspricht der Kotangens dem Quotienten aus Kosinus und Sinus; er ist damit das Längenverhältnis der Ankathete zur Gegenkathete; bei einer Gegenkathete der Länge 1 (Einheitskreis!) entspricht das der x‐Koordinate des Schnittpunktes des Schenkels unseres Winkels mit der waagerechten Tangente am Einheitskreis: Dr. Hempel – Mathematische Grundlagen, trigonometrische Funktionen
Seite 3

der Sekans entspricht dem Reziprokwert des Cosinus, also dem Quotienten aus Hypotenuse und Ankathete. Bei einer Ankathete der Länge 1 (Einheitskreis!) entspricht das der Länge des Schenkels unseres Winkels bis zum Schnittpunkt mit der senkrechten Tangente am Einheitskreis: 
der Kosekans entspricht dem Reziprokwert des Sinus, also dem Quotienten aus Hypotenuse und Gegenkathete. Bei einer Gegenkathete der Länge 1 (Einheitskreis!) entspricht das der Länge des Schenkels unseres Winkels bis zum Schnittpunkt mit der waagerechten Tangente am Einheitskreis: Dr. Hempel – Mathematische Grundlagen, trigonometrische Funktionen
Seite 4
Additionstheoreme  kein Additionstheorem, aber gern und häufig genutzt wird ein Zusammenhang, der aus dem Satz des Pythagoras folgt: sin 2   cos 2   1 Mindestens genauso häufig und gern genutzt werden Formeln, welche die trigonometrischen Funktionen von Winkelsummen und ‐differenzen angeben, die sogenannten Additionstheoreme:  sin(   )  sin  cos   sin  cos   sin(   )  sin  cos   sin  cos  sin(   )  sin(   )  sin 2  cos 2   cos 2  sin 2  
  (1  cos 2  ) cos 2   cos 2  (1  cos 2  )   cos 2   cos 2 


cos(   )  cos cos   sin  sin  cos(   )  cos  cos   sin  sin   cos(   )  cos(   )  cos 2   sin 2  Ein Beweis kann mit Hilfe der Formel von Euler‐Moivre (siehe unten) e i  cos   i  sin  geführt werden: cos(   )  i  sin(   )  e i (   )
 e i  e i
 (cos   i  sin  )(cos   i  sin  )
 (cos   cos   sin   sin  )  i  (sin   cos   sin   cos  )
Ein Vergleich der reellen sowie der imaginären Komponente ergibt die oben dargestellten Additionstheoreme für Sinus und Kosinus. 



tan   tan 
sin(   )

1  tan  tan  cos(   )
tan   tan 
sin(   )

tan(   ) 
1  tan  tan  cos(   )
tan(   ) 
cot  cot   1 cos(   )

cot   cot 
sin(   )
 (cot  cot   1) cos(   )

cot(   ) 
cot   cot 
sin(   )
cot(   ) 
Dr. Hempel – Mathematische Grundlagen, trigonometrische Funktionen
Seite 5
Formel von Euler‐Moivre, Eulersche Identität: e ix  cos x  i  sin x Wieso? ‐ Wir betrachten die Funktion f ( x) 
cos x  i  sin x
e ix
Die Eulersche Identität besagt, dass f ( x)  1 für alle x gilt. Beweisen lässt sich das, wenn man zeigt, dass  der Nenner nie Null wird,  für mindestens ein ausgewähltes x f ( x )  1 ist. f (x) für alle x konstant, d.h. f ( x)  0 ist. 
Damit wäre gezeigt, dass die Behauptung der Eulerschen Identität stimmt.  Der Nenner ist nie Null, denn es gilt e ix  e  ix  e 0  1 
f (0) 
cos 0  i  sin 0
 1 ‐ für das Argument x  0 ist die Forderung f ( x)  1 erfüllt. e i0
 Betrachten wir die Ableitung der Funktion: f ( x) 
( sin x  i  cos x)  e ix  (cos x  i  sin x)  i  e ix

(e ix ) 2
 sin x  e ix  i  cos x  e ix  i  cos x  e ix  i 2  sin x  e ix

0
(e ix ) 2
Da die Ableitung überall Null ist, ist f (x) konstant und mit Punkt 2: f ( x)  1 . Damit kann die Eulersche Identität als bewiesen gelten. Dr. Hempel – Mathematische Grundlagen, trigonometrische Funktionen
Seite 6
Identitäten Aus den Additionstheoremen lassen sich Identitäten ableiten, mit denen die Summe zweier trigonometrischer Funktionen als Produkt aufgefasst werden kann: 



sin   sin   2 sin
 
 cos
 
2
2
 
 
 sin
sin   sin   2 cos
2
2
 
 
 cos
cos   cos   2 cos
2
2
 
 
 sin
cos   cos   2 sin
2
2




sin(   )
cos   cos 
sin(   )
tan   tan  
cos   cos 
sin(   )
cot   cot  
sin   sin 
 sin(   )
cot   cot  
sin   sin 
tan   tan  
Produkte der Winkelfunktionen In Umkehrung zu den eben beschriebenen Identitäten lassen sich Produkte der trigonometrischen Funktionen unter Verwendung ihrer Summe und Differenzen darstellen: 





1
sin   sin   [cos(   )  cos(   )] 2
1
cos   cos   [sin(   )  sin(   )] 2
1
sin   cos   [sin(   )  sin(   )] 2
tan   tan 
tan   tan 
tan   tan  

cot   cot 
cot   cot 
cot   cot 
cot   cot 
cot   cot  

tan   tan 
tan   tan 
tan   cot 
tan   cot 
tan   cot  

cot   tan 
cot   tan 
Dr. Hempel – Mathematische Grundlagen, trigonometrische Funktionen
Seite 7
Umkehrfunktionen  Mit jeder der vorgestellten trigonometrischen Funktionen lässt sich einem vorgegebenen Winkel ein Funktionswert zuweisen. Am Einheitskreis wurde das durch entsprechende Streckenabschnitte veranschaulicht.  Umgekehrt erscheint es häufig nützlich, die umgekehrte Zuordnung vorzunehmen ‐ man weist einer physikalischen Größe (am Einheitskreis z.B. eine Strecke) einen Winkel zu. Dabei gibt es allerdings ein Problem: Als Funktion ist eine Zuordnung nur dann zulässig, wenn sie eindeutig ist. Das funktioniert z.B. bei der Bildung des Sinus ganz gut. Jedem Winkel wird ein Funktionswert zugeordnet ‐ diese sind allerdings für ausgewählte Winkelwerte gleich. Dreht man nun die Zuordnung um, müsste man dem gleichen Wert (hier Streckenabschnitt am Einheitskreis) mehrere Winkelwerte zuweisen. Das geht natürlich nicht. Daher die Forderung: Im Bereich, in dem eine Umkehrfunktion gebildet werden soll, muss der anfängliche funktionale Zusammenhang eineindeutig sein!  Diese Forderung nach Eineindeutigkeit ist jeweils nur für ausgewählte Intervalle des Definitionsbereichs einer trigonometrischen Funktion erfüllt.  Aus der Grafik lässt sich entnehmen, dass der Sinus z.B. im Intervall zwischen   / 2 ... / 2 eineindeutig ist. Für den Kosinus trifft das im Intervall 0 ... zu und für den Tangens zwischen ‐
  / 2 ... / 2 . 


In diesen Bereichen sollten die genannten Funktionen also eine Umkehrfunktion haben; die Zuordnung Strecke  Winkel sollte also funktionieren. Die Umkehrfunktionen werden Arkusfunktionen genannt. Der Name wurde gewählt, weil der Funktionswert einen Winkel darstellt, der häufig im Bogenmaß (Arcus = Bogen) ausgedrückt wird. Entsprechend heißen die Umkehrfunktionen: arcsin  , arccos , arctan  , arc cot  , arc sec  , arccsc . Entstanden sind diese Umkehrfunktionen durch Vertauschen der Zuordnung von unabhängiger und abhängiger Variable; die grafische Darstellung der Umkehrfunktionen sollte sich (im Definitionsbereich!) also auch durch Vertauschen von Abszisse  Ordinate gewinnen lassen. Stellt man danach die unabhängige Variable wieder auf der Abszisse und die abhängige auf der Ordinate dar, hat man die Lösung. In der Grafik lässt sich das durch Spiegelung des Ausgangsgraphen an der Funktion y  x erreichen. Dr. Hempel – Mathematische Grundlagen, trigonometrische Funktionen
Seite 8
Umkehrfunktionen der trigonometrischen Funktionen (Grafik) Dr. Hempel – Mathematische Grundlagen, trigonometrische Funktionen
Seite 9
Für die Arkusfunktionen gelten unter anderem folgende Formeln:  sin(arcsin( ))   ; cos(arccos( ))   ; tan(arctan( ))   ; cot(arc cot( ))   
sin(arccos( ))  1   2 denn mit y  arccos( )  sin y  1  cos 2 y 
cos(arcsin( ))  1   2 denn mit y  arcsin( )  cos y  1  sin 2 y 
sin(arctan( )) 

1  2
denn mit y  arctan( )  sin y 
tan y
1  tan 2 y

cos(arctan( )) 
1
1  2
denn mit y  arctan( )  cos y 
1
1  tan 2 y
Dr. Hempel – Mathematische Grundlagen, trigonometrische Funktionen
Seite 10