PDF, 78,3 KB - ITP, TU Berlin

Quantum Computation:
Zusammenfassung der 11. Vorlesung (08. u. 15.07.2011)
2.3 Ordnungsbestimmung
2.3.1 Die Ordnung einer Restklasse modulo M
Sei M eine natürliche Zahl und x ∈ Z, dann gibt es eine ganze Zahl,
k ∈ Z, so dass
kM ≤ x < (k + 1)M
bzw. x = kM + r,
0 ≤ r < M.
Bei Division von x durch M bleibt ein positiver Rest r. Als eine Restklasse
modulo M bezeichnet man die Menge derjenigen x ∈ Z, für die bei Division
durch M der gleiche positive Rest r übrig bleibt. Die Restklassen modulo M
sind durch die Relation
x ∼M y
:⇔
(∃k ∈ Z) x − y = kM,
die offenbar reflexiv, symmetrisch uns transitiv ist, also eine Äquivalenzrelation
bildet. Für jede natürliche Zahl M zerfällt Z deshalb in die Vereinigung disjunkter Restklassen modulo M, [x]M . Da jede Restklasse genau ein Element
r mit 0 ≤ r < M enthält, das die Klasse repräsentiert, [x]M = [r]M , gibt es
genau M Restklassen modulo M.
Algebraisch bilden die Restklassen modulo M einen Ring. Die Addition
[x]M + [y]M ; = [x + y]M
definiert eine Klassenoperation, d,h, es ist gleichgültig, mit welchen Elementen z ∈ [x]M und z ′ ∈ [y]M die Summe gebildet wird, sie ist stets die
Klasse [x+y]M . Die Addition ist offenbar assoziativ, kommutativ, das netrale
Element ist [0]M und das Inverse von [x]M ist [−x]M . Die Multiplikation
[x]M [y]M := [xy]M
definiert ebenfalls eine Klassenoperation, denn mit z ∈ [x]M , z ′ ∈ [y]M gelten
xy = (kx M + rx )(ky M + ry ) = (kx ky M + rx ky + kx ry )M + rx ry
1
und
zz ′ = (kz M + rx )(kz′ M + ry ) = (kz kz′ M + rx kz′ + kz ry )M + rx ry ,
so dass die Differenz xy − zz ′ (ohne Rest) durch M teilbar ist. Offenbar ist
die Multiplikation auch assoziativ, kommutativ, und [1]M ist das neutrale
Element. Offenbar gilt auch das Distributivgesetz
[x]M ([y]M + [z]M ) = [x]M [y]M + [x]M [z]M .
Damit bilden die Restklassen modulo M algebraisch einen Ring. Der Bequemlichkeit halber wird auch
x = z modM
anstelle von [x]M = [z]M
geschrieben.
Um die Frage nach der Existenz von inversen Elementen für die multiplikative Halbgruppe eines Restklassenringes zu beantworten, führen wir den
Begriff eines Moduls ganzer Zahlen ein: Eine Teilmenge
S ⊆ Z heißt Modul, falls x, y ∈ S ⇒ x ± y ∈ S
gilt. Speziell ist die Menge {0} ein Modul, der Nullmodul. Die Null ist in
einem Modul wegen x − x ∈ S stets enthalten. Mit k ∈ Z und x ∈ S ist auch
kx ∈ S. Sind k, l ∈ Z und x, y ∈ S, dann sind auch kx + ly ∈ S. Ist S =
̸ {0},
dann gilt S ∩ N ̸= ∅, und diese Menge enthält ein kleinstes Element:
(∃ d ∈ S ∩ N)(∀a ∈ S) 0 ≤ a < d ⇒ a = 0.
Für diese Zahl d gilt nun die folgende
Behauptung: x ∈ S ∩ N ⇒ (∃ n ∈ N) x = nd.
Beweis:
x = nd + c, 0 ≤ c < d
⇒ c = x − nd ∈ S
}
⇒ c = 0.
Damit haben wir gezeigt
Satz: Sei S =
̸ {0}, dann gibt es ein d ∈ S ∩ N, so dass für jedes Element
x ∈ S ein k ∈ Z existiert mit x = kd, also S = {kd|k ∈ Z}. Insbesondere ist
jedes Element von S (ohne Rest) durch d teilbar.
2
Im Folgenden werden wir für die Teilbarkeit (ohne Rest) ein Symbol verwenden. Sei c ∈ N und a ∈ Z, wir schreiben
c|a
:⇔
(∃k ∈ Z) a = kc
und nennen a durch c teilbar.
Definition: Sei d ∈ N, a, b ∈ Z. Wir schreiben
(a, b) = d
:⇔
d|a ∧ d|b ∧ .(∀c > d) c̸ | a ∨ c̸ | b.
und nennen d den größten gemeinsamen Teiler (ggT) von a und b.
Offenbar ist S(a, b) := {ka + lb|k, l ∈ Z} ein Modul und damit existiert
ein d′ ∈ N mit S(a, b) := {kd′ |k ∈ Z}. Jedes Element von S(a, b) ist durch
d′ teilbar, also auch a und b. Somit gilt d′ ≤ d = (a, b). Andererseits gilt d|a
und d|b und damit d|ka + lb für k, l ∈ Z, also gilt d|x für alle x ∈ S(a, b),
insbesondere gilt d|d′ . Damit ist auch d ≤ d′ , also d = d′ . Damit haben wir
den folgenden Satz bewiesen.
Satz: S(a, b) := {kd|d = (a, b), k ∈ Z}.
Aus diesem Satz folgen unmittelbar:
Satz: Seien a, b, c ∈ Z, (a, b) = d dann gilt
(∃ x, y ∈ Z) xa + yb = c
⇔
d|c.
Insbesondere gilt (a, b) = d = x′ a + y ′ b, x′ , y ′ ∈ Z.
Satz: Jeder gemeinsame Teiler von a und b ist ein Teiler von d = (a, b).
Wir können nun die Frage beantworten, welche Elemente [x]M des Restklassenringes modulo M invertierbar sind. Es gilt
[x]M [y]M = [1]M ⇔ (∃k ∈ N) yx + kM = 1 ⇔ .1 = ld, l ∈ Z. ⇔ d = 1,
wobei d = (x, M ) ist. Damit gilt:
Satz: [x]M ist genau dann invertierbar, wenn (x, M ) = 1 ist. Insbesondere
ist der Restklassenring modulo M ein Körper genau dann, wenn M eine
Primzahl ist.
Die im vorletzten Absatz aus den Eigenschaften eines Moduls ganzer
Zahlen gefolgerten Sätze erlauben den Beweis zweier grundlegender Theoreme. Als Primzahlen werden bekanntlich die von 1 verschiedenen natürlichen
3
Zahlen bezeichnet, die keinen von 1 verschiedenen Teiler haben. Das folgende
Theorem wird auch der “erste Euklidische Satz” genannt.
Satz (Euklid): Sei p eine Primzahl und a, b ∈ Z, dann gilt
p|ab
⇔
.p|a ∨ p|b.
Beweis: Sei p|ab und etwa p̸ | a, dann gilt (a, p) = 1 und damit gibt es ganze
Zahlen x und y mit xa + yp = 1. Folglich gilt xab + ypb = b. p|ab und p|pb
führen sofort auf p|b.
Jede von 1 verschiedne natürliche Zahl n ist trivialerweise ein Produkt von
von Primzahlen. Schreibt maan
n = pa11 pa22 pa33 . . . paNN ,
p1 < p2 < p3 < · · · < pN ,
ai > 0,
dann heißt dies die Standarddarstellung der Primfaktorzerlegung. Aus dem
ersten Euklidischen Satz folgern wir nun:
Satz: Die Primfaktorzerlegung einer Zahl 1 < n ∈ N ist eindeutig.
Beweis: Seien
bM
n = pa11 pa22 pa33 . . . paNN = q1b1 q2b2 q3b3 . . . qM
Standarddarstellungen. Da qj |n muss nach dem Satz von Euklid mindestens
∑
einer der N
1 ai “p”-Primfaktoren durch qj teilbar und damit gleich qj sein.
Damit folgt {qj }j=1,2,...,qM ⊆ {pi }i=1,2,...,qN . Analog zeigt man {pi }i=1,2,...,qN ⊆
{qj }j=1,2,...,qM . Aus der Gleichheit der Mengen folgt M = N und aus der
Stadardanordnung pi = qi . Nehmen wir an ai < bi , dann folgt für n/pai i
sowohl p1 |(n/pai i ) als auch p1̸ |(n/pai i ), ein Widerspruch. Ebenso ist abi < ai
nicht möglich, also gilt ai = bi .
Wir beweisen weitere für uns nützliche allgemeine Sätze. Im Beweis des
ersten Satzes von Euklid haben wir gezeigt, dass für k ∈ N
ab
∈ Z ∧ (a, k) = 1 . ⇒ .
k
b
∈Z
k
ist, wobei k nicht notwendig eine Primzahl sein muß. Diese Aussage findet
auch im folgenden Theorem Anwendung.
4
Satz: Sei (x, M ) = d, dann gilt
xy = xz modM
⇔
y = z mod
M
.
d
Beweis: Es gilt
x = kd,
M = Kd,
(k, K) = 1,
letzteres, weil andernfalls d nicht der größte gemeinsame Teiler wäre, was
vorausgesetzt wurde. Es folgt
Z∋
xy − xz
kd(y − z)
k(y − z)
=
=
M
Kd
K
⇔
(y − z)
∈ Z,
K
weil (k, K) = 1. Aus K = M/d folgt die Behauptung.
Satz: Sei (x, M ) = 1 und {[ym ]M }m=0,1,...,M −1 ein vollständiges System von
Restklasssen modulo M . Dann ist auch {[xym ]M }m=0,1,...,M −1 ein vollständiges
System von Restklasssen modulo M .
Beweis: Wegen (x, M ) = d = 1 ist nach dem vorsthenden Satz x(ym − yn ) =
0 (modM ) äquivalent zu ym − yn = 0 modM . Da letzteres mur für m = n
gelten kann, folgt die Behauptung.
Alternativ kann man auch argumentieren, dass für (x, M ) = 1 die Abbildung
[z]M 7→ [xz]M eine Bijektion der Restklassen modulo M auf sich ist, weil [x]M
invertierbar ist.
Satz:Sei (a, M ) = d, dann ist die Gleichung
ax = b modM
genau dann lösbar, wenn d Teiler von b ist. Sie hat genau d modulo M
verschiedene Lösungen. Speziell ist sie eindeutig lösbar, wenn d = 1 ist
und insbesondere ist in diesem Fall das Inverse von a modM die Lösung von
ax = 1 modM .
Beweis: Wir haben oben gezeigt
(a, M ) = d ⇒ .(∃ x, y ∈ Z) ax + M y = b ⇔ d|b. .
Wegen b = ax + M y = ax mod M ist dies die erste Behauptung des Satzes.
Für d = 1 ist ax = b modM stets lösbar, und, da [a]M invertierbar und
5
−1
[a]M
[b]M = [x]M ist, ist die Lösung modulo M eindeutig. Für d > 1 und d|b
seien a = da′ , M = dM ′ und b = db′ . Dann gilt
ax = b modM
a′ x = b′ modM ′ ,
⇐⇒
und, weil (a′ , M ′ ) = 1 ist, hat die Gleichung mit den gestrichenen Koeffizienten eine eindeutige Lösung. Diese sei x′ modM ′ . Modulo M sind aber
x′ modM, (x′ + M ′ ) modM, (x′ + 2M ′ ) modM, . . .
. . . , (x′ + (d − 1)M ′ ) modM
d paarweise verschiedene Lösungen der ursprünglichen Gleichung.
Die Eulersche Funktion ϕ : Z → N gibt tdie Anzahl der paaerweise verschiedenen Restklassen [x]M mit (x, M ) = 1, d.h. die Anzahl der der invertierbaren Elemente des Restklassenringes modulo M an. Nstürlich gilt
dafür auch der Satz:
Satz: Ist {xi }i=1,2,3,...,ϕ(M ) ein vollständiges System invertierbarer Restklassen und ist (y, M ) = 1, dann ist auch {yxi }i?1,2,3,...,ϕ(M ) ein solches System.
Für die Eulersche Funktion gilt nun der Satz:
Satz: Wenn (y, M ) = 1 ist, gilt
y ϕ(M ) = 1 modM.
Beweis: Für ein vollständiges System invertierbarer Restklassen {[xi ]M }i=1,2,3,...,ϕ(M )
und (y, M ) = 1, dann gilt
∏
ϕ(M )
∏
ϕ(M )
yxi =
i=1
xi modM,
i=1
weil auf beiden Seiter der Gleichung das Produkt der invertierbaren Elemente
des Restklassenringes steht. Somit gilt
∏
ϕ(M )
y
ϕ
i=1
∏
ϕ(M )
xi =
i=1
6
xi modM,
und weil das Produkt invertierbarer Restklassen modulo M invertierbar ist
folt die behauptete Gleichung
y ϕ(M ) = 1 modM.
Definition: Sei (x, M ) = 1, dann heißt rM (x) = min{l ∈ N|xl = 1 modM }
die Ordnung der Restklasse [x]M , oder kurz die Ordnung von x modulo M .
Offenbar gilt 1 ≤ rM (x) ≤ ϕ(M ). Offenbar ist
MM (x) := {n ∈ Z | xn = 1 modM } ̸= {0}
ein Modul ganzer Zahlen, denn mit m, n ∈ MM (x) ist m ± n ∈ MM (x),
und es gibt ein 0 < d ∈ MM (x) mit m MM (x) → m = kd, k ∈ Z. Es ist
also rM (x) = d, das kleinste positive Element von MM (x) und der größte
gemeinsame Teiler aller Elemente von MM (x). Insbeondere ist ϕ(M ) ∈
MM (x) und damit gilt rM (x)|ϕ(M ). Für Primzahlen P ist ϕ(P ) = P − 1,
denn alle von [0]P verschiedenen Restklassen modulo P sind invertierbar.
Damit haben wir gezeigt:
Satz: Sei (x, M ) = 1, dann ist die Ordnung rM (x) von x modulo M ein
Teiler von ϕ(M ), rM (x)|ϕ(M ). Für Primzahlen P gilt rP (x)|P − 1.Es gilt
xn = 1 modM je nach dem, ob n = krM (x), k ∈ Z, wahr ist oder nicht.
Einige Beispiele sollen das Vorstehende illustrieren:
22 = 1 mod 3
22 = 0 mod 4
24 = 1 mod 5
22k+1 = 2 mod 6
22k = 4 mod 6
(5, 21) = 1 56 = 1 mod 21
(2, 3) = 1
(2, 4) = 2
(2, 5) = 1
(2, 6) = 2
r3 (2) = 2
[2]2 ist “nilpotent”
r5 (2) = 4
r21 (5) = 6
Klassische Algorithmen zur Ordnungsbestimmung sind von exponentieller
Dauer.
2.3.2 Ordnungsbestimmung und Phasenbestimmung
Jede Restklasse modulo M , [x]M , liegt durch Rest bei Division von x
durch M , 0 ≤ rx < M , rx ∈ [x]M , bzw. rx = x modM , fest. Es gilt
7
rx = [0, M − 1] ∩ [x]M . Ist {|k)}k=0,1,2,...,(M −1) eine Orthonormalbasis im CM ,
dann definiert jede Restklasse [x]M mit x • k := [0, M − 1] ∩ [xk]M durch
|k) 7−→ |x • k)
eine lineare Transformation auf CM . Für (x, M ) = 1 ist diese Transformation
unitär.
Satz:Sei (x, M ) = 1, dann ist die lineare Transformation
Ux : CM
|k)
−→
7−→
CM
|x • k)
unitär. Ist r := rM (x) die Ordnung von x modulo M und gilt (y, M ) = 1,
dann sind
r−1
1 ∑ − 2πi ls l
√
χs (y) =
e r |x • y)
r l=0
Eigenvektore n von Ux zum Eigenwert e
2πi
s
r
, (s=0,1,2,. . . ,r-1). Schließlich gilt
1 ∑
|y) = √
χs (y).
r s=0
r−1
Beweis: Ux ist unitär, weil für (x, M ) = 1 das vollständige System [k]M , (k =
0, 1, 2, . . . , M − 1) von Restklasssen modulo M auch [xk]M ein vollständigen
System von Restklassen ist, so dass die Basisvektoren nur permutiert werden.
Weiterhin ist
r−1
1 ∑ − 2πi ls l+1
Ux χs (y) = √
e r |x • y)
r l=0
1 ∑ − 2πi (l−1)s l
= √
e r
|x • y)
r l=1
( r−1
)
∑ 2πi
2πi
2πi
1
= e r s√
e− r ls |xl • y) + e− r rs |xr • y)
r l=1
( r−1
)
∑ 2πi
2πi
2πi
1
= e r s√
e− r ls |xl • y) + e− r 0s |(1 • y)
r l=1
r
2πi
1 ∑ − 2πi ls l
√
e r |x • y) = e r s χs (y),
r l=0
r−1
= e
− 2πi
s
r
8
damit sind die χs (y) Eigenvektoresn von Ux zum Eigenwert e
1). Schließlich ist
2πi
s
r
, (s=0,1,2,. . . ,r-
1 ∑ ∑ − 2πi ts t
1 ∑
√
χs (y) =
e r |x • y)
r s=0 t=0
r s=0
r−1
r−1 r−1
=
=
r−1
r−1
∑
1∑
t=0
r−1
∑
r
e−
2πi
ts
r
|xt • y)
s=0
δt0 |xt • y) = |1 • y) = |y)
t=0
Die Aussagen dieses Theorems erlauben nun, die Ordnungsbestimmung
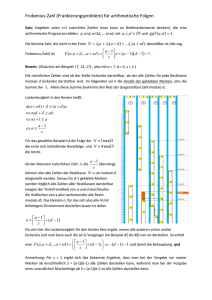
mit Hilfe der Phasenbestimmung zu erreichen. Um die Ordnung von x modulo M zu bestimmen, muss man zunächst Ux : CM → CM implementieren.
Dazu benötigt man ein Register mit In L = [log2 M ] Qubits, 2L−1 < M ≤ 2L .
Die Quantenalgorithmen der Grundrechenarten reichen dann aus, um x•k zu
berechnen und damit Ux ⊕ 12N −(M +1) reversibel zu implementieren. Da r unbekannt ist , hat man jedoch nicht χs (y) als Eingabe im zweitn Register der
L
Phasenbestimmung
zur Verfügung, sondern nur |y)L ∈ C2 mit (y, M ) = 1,
∑
etwa |1)L = √1r r−1
s=0 χs (1). Der Algorithmus
|0 >
H
···········
|0 >
H
···········
|0 >
N Stk. H
|0 >
H
···
···
···
···
··
|0 >
H
s
C
2L
∋ |y)L
20
Ux
···
···
···
····
s
···········
···········
s
s
····
····
·
····
····
·
···········
21
Ux
F+
N
Ψ̌
N
2N −2
··········· Ux
2N −1
Ux
|y)L
∑2N −1
s
würde bei Eingabe von χs (y) den Zustand
k=0 ak ( r )|k)N liefern, mit
s
s
N
ak ( r ) = δk rs falls 2 r ∈ N. Letzteres ist jedoch nicht zu erwarten, so
dass man mit einem Fehler gemäß Abschnitt 2.3.1 rechnen muss. Auf eine
geeignete Eingrenzung des Fehlers durch Wahl von N kommen wir noch
9
zurück. Sie wird durch ein Theorem über die Approximation rationaler
Zahlen
∑r−1durch Kettenbrüche festgelegt. Da anstelle von χs (y) nur |y)L =
√1
s=0 χs (y) eingegeben werden kann, liefert der Algorithmus
r
r−1 2∑
−1
∑
N
Ψ̌N =
s=0 k=0
s
ak ( )|k)N .
r
∑
Das Ergebnis κ der Messung von A = k 2kN |k)(k| am ersten Register ist
eine rationale Zahl, da nur 2N Stellen hinter dem Komma zur Verfügung
stehen. Die zu bestimmende Zahl ist auch eine rationale Zahl, rs , wobei der
Nenner oder ein Vielfaches des Nenners die gesuchte Ordnung von x modulo
M sein kann. Das Verfahren besteht nun darin, dass der Messwert κ in
einen einfachen Kettenbruch endlicher Länge G entwickelt wird, der etwa
mit G = 4 die Gestlt
1
κ = ao +
=: [a0 a1 a2 a3 aG ],
1
a1 +
a2 +
1
a3 +
1
aG
hat, wobei a0 = 0 wegen 0 ≤ κ < 1 und aj ∈ N für j ≥ 1 gilt. Dadurch liegen
G Näherungsbrüche κ1 = [0a1 ] = a11 , κ2 = [0a1 a2 ] = pq22 , κ3 = [0a1 a2 a3 ] =
p3
G−1
, κG = [0a1 a2 a3 . . . aG ] = pqGG , wobei
, . . . , κG−1 = [0a1 a2 a3 . . . aG−1 ] = pqG−1
q3
pj , qj ∈ N und (pj , qj ) = 1 gelten, fest. Diese Entwicklung und die Nenner der
Näherungsbrüche lassen sich klassisch mit einem Algorithmus polynomialer
Dauer erhalten. Erstaunlicher Weise lässt sich zeigen, dass rs mit einem dieser
Näherungbrüche übereinstimmt, wenn nur der Messwert κ um weniger als
1
von rs abweicht, d.h. |κ − rs | < 2r12 gilt. Nun ist r < M , so dass diese
2r 2
Voraussetzung bei Wahl der maximalen Abweichung ϵ ≤ 2M1 2 < 2r12 für ein
s
, s = 1, 2, 3, ,̇N − 1 erfüllt sein muss. Die Ordnung r von x modulo M
r
ist dann also der Nenner oder, wegen (pn , qn ) = 1, ein ganzes Vielfaches
des Nenners von einem der Näherungsbrüche des Messwertes κ. Dies gilt
allerdings nur mit einer gewissen Wahrscheinlichkeit, die noch abzuschätzen
ist. Man prüft mit einem klassischen Agorithmus mit polynomialer Dauer,
ob eine der Zahlen mqj , m = 1, 2, 3, . . . , M2 , j = 1, 2, 3, . . . , G die Ordnung
von x modulo M ist. Wenn man die Ordnung nicht findet, muss man κ
verwerfen und neu beginnen.
10