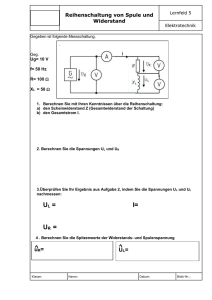
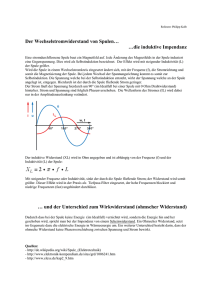
Wechselstromkreise

Einschaltvorgänge in
Stromkreisen mit Kondensatoren,
Spulen und Widerständen
Einschaltvorgänge für klassische
Kombinationen der drei Bauelemente
Inhalt
• Spannungen im Stromkreis beim
Einschalten
– Reihenschaltung von Kapazität und
Widerstand
– Reihenschaltung von Induktivität und
Widerstand
Kondensator und Widerstand in Reihe
Q(t )
U C (t ) 
C
Uc
U R (t )  R  I (t )
UR
I
U0
Analyse nach der Kirchhoffschen Maschenregel, Umlauf von +
nach -, Quellen von + nach – zählen positiv, im Gegensinn
durchlaufene negativ
UC  Q / C
U R  RI
U0
U0
0  U C  U R  U 0
0  Q / C  R  I  U 0
Spannungen über den Bauteilen
beim Einschalten einer Gleichspannung
Q(t )
U (t ) 
C
1V
Kapazitiv
U (t )  R  I (t )
1V
Ohmsch
Spannungen im Stromkreis beim Einschalten
einer Gleichspannung U0
Q (t )
dQ (t )
U0 
R
C
dt
t


Q(t )  Q0 1  e 





1V
1C
(Differential-)
Gleichung für die
Ladung am
Kondensator
Lösungs-Ansatz
für die Ladung am
Kondensator
Lösung: Spannungen im RC Stromkreis beim
Einschalten
t


Q0
1  e 
U0 
C 
U0 
1

t

 1
  RQ0e 
 

RQ0
Q0
U0 
C
1
1

RC
  RC
1 V Ansatz eingesetzt
1 V Speziell: t=0
1 V Speziell: t=∞
1
Zeile 2 dividiert
durch Zeile 3
1/s Zeitkonstante
Spannung und Ladung am Kondensator,

t
U (t )  Q(t ) / C  U 0 (1  e  )
B
Ladung am Kondensator
1,0
0,8
0,6
0,4
0,2
0,0
0,0
0,2
0,4
0,6
Zeit [s]
0,8
1,0
B
Spannung am
Kondensator
Spannung am Kondensator [V]
1,0
0,8
0,6
0,4
0,2
0,0
0,0
0,2
0,4
0,6
0,8
1,0
Zeit [s]
Uc
0
-1
1
1F
0,3 Ω
I
-1
U0
0
UR
1
Spannung am Widerstand
Uc
0
-1
1
C
1F
0,3 Ω
I
-1
U0
0
UR
1
Spannung am Widerstand [V]
1,0
0,5
0,0
0,0
0,2
0,4
0,6
Zeit [s]
0,8
1,0
B
Spannung an
Kondensator und
Widerstand
Spannung am Kondensator [V]
1,0
0,8
0,6
0,4
0,2
0,0
0,0
0,2
0,4
0,6
0,8
1,0
Zeit [s]
Uc
0
-1
1
C
1F
0,3 Ω
I
-1
U0
0
UR
1
Spannung am Widerstand [V]
1,0
0,5
0,0
0,0
0,2
0,4
0,6
Zeit [s]
0,8
1,0
Spule und Widerstand in Reihe
UL
UR
I
U0
Vorzeichen der Spannung an einer Spule bei Anschluss an eine
Spannungsquelle
U L  ( L  I(t ))
U R  RI
U~
U0
*Bei
Anschluss einer Spule an eine Spannungsquelle stellt
sich der Strom so ein, dass die durch sein Magnetfeld
induzierte Spannung gleich der Spannung an der Quelle
ist: Das Vorzeichen der Spannung an der Quelle (es sei links
momentan „Plus“) überträgt sich deshalb auf die Spule
Einschaltvorgang an einer Gleichspannungsquelle: Analyse nach der
Maschenregel, Umlauf von + nach -, Quellen von + nach – zählen positiv,
im Gegensinn negativ
U L  ( L  I(t ))
U R  RI
U0
U0
0  U L  U R  U 0
0  ( L  I(t ))  R  I (t )  U 0
Spannungen über den Bauteilen
beim Einschalten einer Gleichspannung
U (t )  LI(t )
1V
Induktiv
U (t )  R  I (t )
1V
Ohmsch
Spannungen im Stromkreis beim Einschalten
einer Gleichspannung U0
U 0  L  I(t )  R  I (t )
t


I (t )  I 0 1  e 





(Differential-)
Gleichung für den
1V
Strom durch
Widerstand und Spule
Lösungs-Ansatz für
1A
den Strom
Lösung: Spannungen im LR Stromkreis beim
Einschalten
U0 
LI 0

e

t

t


 RI 0 1  e 





1 V Ansatz eingesetzt
LI 0
1 V Speziell: t=0
U 0  RI 0
1 V Speziell: t=∞
U0 

1L
1
 R
L

R
1
Zeile 2 dividiert
durch Zeile 3
1/s Zeitkonstante
Spannung an der Spule
U (t )  L  I(tC)  U 0e
Spannung an der Spule [V]
1,0
0,5
0,0
0,0
0,2
0,4
0,6
Zeit [s]
0,8
1,0

t

C
Spannung an der Spule
Spannung an der Spule [V]
1,0
0,5
0,0
0,0
0,2
0,4
0,6
0,8
1,0
Zeit [s]
UL
0
-1
1
1H
0,3 Ω
I
U0
Spannung am Widerstand
1H
B
0,3 Ω
I
-1
U0
0
UR
1
Spannung am Widerstand [V]
1,0
0,8
0,6
0,4
0,2
0,0
0,0
0,2
0,4
0,6
Zeit [s]
0,8
1,0
Spannung an Spule und
Widerstand
C
Spannung an der Spule [V]
1,0
0,5
0,0
0,0
0,2
0,4
0,6
0,8
1,0
Zeit [s]
Uc
0
-1
1
1H
B
0,3 Ω
I
-1
U0
0
UR
1
Spannung am Widerstand [V]
1,0
0,8
0,6
0,4
0,2
0,0
0,0
0,2
0,4
0,6
Zeit [s]
0,8
1,0
Zusammenfassung
• Bei Kombination von Widerständen mit Kondensatoren steigt
nach dem Einschalten die Spannung über dem Kondensator
mit 1-EXP(-t/τ)
– Die charakteristische Zeit zum Anstieg auf den Teil (11/e)=0,63 ist die Zeitkonstante τ =RC [s]
• Bei Kombination von Widerständen mit Spulen fällt nach dem
Einschalten die Spannung über der Spule wie EXP(-t/τ)
– Die charakteristische Zeit zum Abfall auf den Teil
(1/e)=0,37 ist die Zeitkonstante τ = L/R [s]
C
finis
Spannung an der Spule [V]
1,0
0,5
0,0
0,0
0,2
0,4
0,6
0,8
1,0
Zeit [s]
Uc
0
-1
1
1H
B
0,3 Ω
I
-1
U0
0
UR
1
Spannung am Widerstand [V]
1,0
0,8
0,6
0,4
0,2
0,0
0,0
0,2
0,4
0,6
Zeit [s]
0,8
1,0