Die Winkel-Wichtel - hr

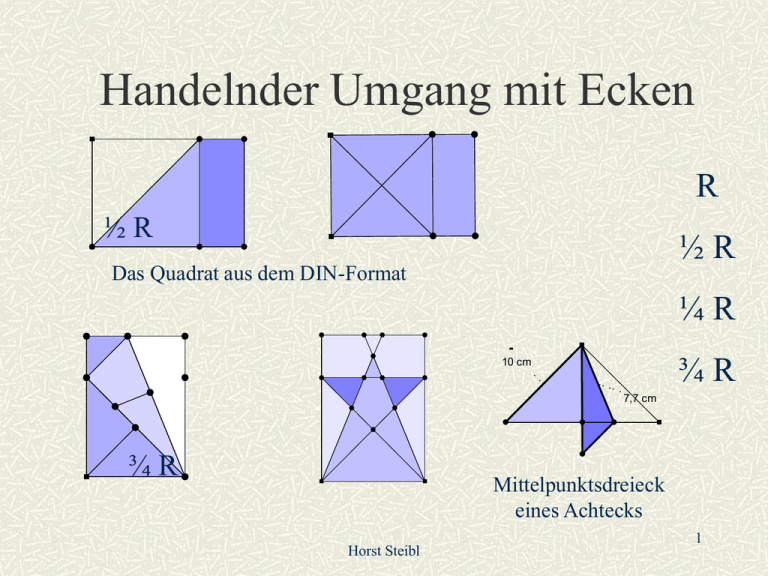
Handelnder Umgang mit Ecken
R
½R
½R
Das Quadrat aus dem DIN-Format
¼R
10 cm
¾R
7,7 cm
¾R
Mittelpunktsdreieck
eines Achtecks
Horst Steibl
1
Das gleichseitige Dreieck im Quadrat
1/ R
3
2/ R
3
Drittelung von R
4/ R
3
Das Rechteck über dem
gleichseitigen Dreieck
Das 3-Rechteck als Modul für Körper
aus gleichseitigen Dreiecken
Horst Steibl
2
Tangram
Spitze und stumpfe Ecken
stumpfe Ecke auf
gegenüberliegende rechte Ecke
spitze Ecke
auf benachbarte rechte Ecke
Horst Steibl
3
Das Flachsmeyersche Fünfeck
Mittelsenkrechte
der Diagonalen
und die Diagonale
Die
Winkelhalbierende
des Teilwinkels
von 35,3°36°
Horst Steibl
4
1/
5
R als Winkelmaß
Die Diagonale teilt den rechten
Winkel in 35,3...° + 45,6...°
Halbieren Sie die 36° Winkel,
so ergibt sich eine Fünftelung
von R.
Z3
Z4
Falten Sie zum Fächer
Zur vierseitigen Pyramide
Z1
Z2
Schlagen Sie Kreise um die
Endpunkte der Diagonalen und
legen Sie vier dieser Kreisviertel
zum Vollkreis
Horst Steibl
5
Das geviertelte Quadrat
Vom Schaufelrad zum Quadrat mit Loch
Horst Steibl
6
4,2 cm
4,2 cm
Auf einer Linie mit möglichst vielen Zacken
Wenig Zacken,
symmetrisch
Horst Steibl
7
Wann schließen sich vier Winkel zum Vollwinkel?
2,7 cm
2,7 cm
cm
Schreibe die Reihenfolge auf:
st, r, sp, r
Suche alle Formen r r r r
Alle r sp st r
Alle r sp st r
Was geschieht, wenn du sp sp sp sp legst?
Kannst du st st st st legen?
Horst Steibl
8
Das viergeteilte Quadrat
winkelgleiche Vierecke
Der Begriff der Ähnlichkeit?
Horst Steibl
9
2 rechte ein spitzer und ein stumpfer Winkel
Nun aber zu den Winkel Wichtel
Horst Steibl
10
Winkel auf dem Geobrett
Gleich spitz?
spitzer als....
Wo liegt bezgl der Seite der spitzeste Winkel?
ein Rechter
Horst Steibl
stumpfer als...
11
Tim und Tom, die Winkel-Wichtel
Das ist Tim. Er ist sehr vorlaut und meint,
er sei der schärfste Winkel-Wichtel, weil
sein Hut der spitzeste sei.
Tim
Und dies ist Tom, er ist ein wenig weiser
als Tim und lässt ihm bezüglich der
Spitze seines Hutes den Vortritt. Aber auf
ihre Hüte sind beide sehr stolz.
Sie hausen in den dreieckigen Zimmern der
Geobrett-Burg. Tim wohnt im (5,11,14) Zimmer, Tom in der (5, 10,11) – Kammer.
Tom
Horst Steibl
12
Horst Steibl
13
Tim und Tom in ihren Kammern
5, 11, 14 - Kammer
5, 10, 11 - Kammer
Horst Steibl
14
Rex, der König der Winkel-Wichtel
Rex zeichnete seine Befehle immer
mit einem großen R ab. Er fand
immer eine rechte Ecke zum
schlafen.
Sein Sohn, der Kleine König, hatte
einen Hut, der halb so spitz wie die
Krone des Königs war. Deshalb
hießt er bei den Wichteln auch der
halbe König
Horst Steibl
15
Wer hat den spitzesten Hut?
Tim meint, er habe den spitzeren Hut:
Tom weiß das zwar auch, aber er
streitet darüber gern mit Tim.
Der Wichtel Tangens, der ein großer Mathematiker
ist, hat sie dann einmal in die (5, 7, 11)-Kammer
eingesperrt. Er meint , wer dort mit den Beinen an
die kürzere Seite zeigt, habe den spitzeren Hut.
Damit war der Streit ausgestanden.
Horst Steibl
16
Die Doppelkammern
m
Tim hat einen Zwillingsbruder, Timm mit
zwei m. Wenn der zu Besuch kommt,
schlafen sie in der Tim-Timm Ecke.
Der Zwillingsbruder von Tom
kommt auch ab und zu. Jetzt
kann man gut sehen,dass sie
Das ist also die Tom-Tom-Ecke
etwas breitere Hüte haben als
17
die Tims.
Horst Steibl
Eckensalat
Die Familien der Tims und der Toms
haben schon immer die Ecken nach
ihren Namen bezeichnet:
Hier siehst du eine TomTimTim-Ecke und eine
TomTimTimTom-Ecke
Horst Steibl
21
18
Horst Steibl
19
Das vergessene Zauberwort der Wichtel
Eines Tages fand Tom ein altes Dokument mit einer
Tabelle und den Grundrissen der Geobrettburg. In der
Tabelle standen untereinander merkwürdige
Buchstabenreihen aus o und i . Im Grundriss waren in
den Ecken der dreieckigen Kammern einzelne
Buchstaben eingezeichnet. Tom grübelte lange darüber,
was das Ganze zu bedeuten habe. Plötzlich kam ihm
eine Idee. Das verschollene Zauberwort. Aber wie
sollte er die Lösung finden?
Horst Steibl
20
Zerlege und du findest das Zauberwort
oiio
oi
N
iooi
K
o
I
A
P
ii
T
R
oiiooi
oo
S
U
A
oiioo
iio
22
Horst Steibl
ooi
21
Zerlege und du kannst die Ecke benennen
o o i
o
o
i
i
o
Eine Tom-Tom-Tim Ecke
Horst Steibl
Eine oiioo-Ecke
22
Zerlege und du findest das Zauberwort
N
K
I
A
P
T
R
S
U
A
Horst Steibl
oiio
P
oi
A
iooi
N
o
K
ES
ii
R
oiiooi
A
oo
T
oiioo
I
iio
U
ooi
23
S
Die Winkelgrößen auf dem Geobrett
iooi
i o
oi
oiioo
Tom fand heraus, dass es
10 Klassen gleich großer
Winkel gibt. Er ordnete
sie der Größe nach:
i o ii oi oo iio ooi
ii
oo
oiio
ooi
iio
oiiooi
oiioo oiiooi
tan a = ½  a = 26,5..°
i= 18,5°
o= 26,5°
ii= 37°
io= 45°
oo=53°
iio= 63,5°
ooi= 71,5°
Horst Steibl
iooi=90°
oiioo=116,5°
oiiooi=135°
24
Ordnen nach der Winkelgröße
Horst Steibl
25
Dreieckswinkel der Größe nach
Horst Steibl
26
Winkelsumme im Dreieck
ii
i i
ioo
Start
ooi
oiioo
io iooiioo
oiioo + i+ io = oiio oiio
Zwei Rechte
ioo + ii + ooi= iooi iooi
Horst Steibl
27
Ein Viereck:
iio
oiio
oiiooi
ioo
oiio oiio oiio oiio
Ergibt sich immer eine oiio Folge wenn ich rings herum die Winkel teile?
Horst Steibl
28
Ein nicht konvexes Viereck
i
iooiiooiio
oi
ioo
oiio oiio oiio oiio
Horst Steibl
29
Welches Dreieck wird durch diese Winkelfolge charakterisiert?
(oi)(iooi) (io)
o)(iio)(oii)(o
(oiio)(oi)(io)
o)(ii)(ooi)(io
(o)(i)(iooiio)
(oiio)(oi)(io)
(oiioo)(i)(io)
(oiio)(o)(iio)
Horst Steibl
30
Nicht jede Folge lässt sich auf einem Brett darstellen
(o)(iio o)(iio)
(oi)(ioo)(iio)
Im Punktegitter lässt sich aber jede dieser
Folgen darstellen
Horst Steibl
31
Vielen Dank für Ihre Aufmerksamkeit
Horst Steibl
32