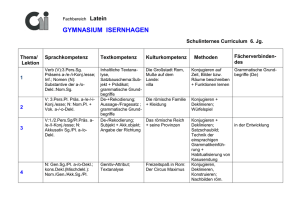
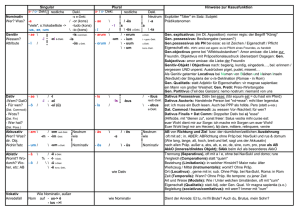
Datenverarbeitung Teil 1

Lösung 7.1
Syntax und Semantik
1. Geben Sie Beispiele für
a) lexikalische Strukturelemente: Bezeichner, Literale, Schlüsselworte, ...
b) syntaktische Strukturelemente: Alle Elemente aus „Algorithmenentwurf“
der Programmiersprache C++ an
2. Formulieren Sie die Semantik
a) einer while-Schleife:
siehe Schleife mit vorausgehender Prüfung
b) eines Unterprogrammaufrufes siehe „Block“
1. recherchieren Sie nach weiteren Programmiersprachen
Algol 60, Algol 68, Forth, PL/1, Fortran, Smalltalk, Simula 67, SETL,
Snobol, Cobol, Pascal, Turbo-Pascal, DELPHI, Concurrent Pascal, SPSS,
CLU, Alphard, SDL, Oberon, Oberon-2, Object Cobol, Ada, APL, CDL 2,
Ada 95, Mesa, Modula-2, Chill, BCPL, C, Objective-C, Modula-3, C++,
,Assemblersprachen, Prolog, Prolog II, Eiffel, Beta, Opal, CS,P Hope,
Miranda, Lisp, Common Lisp, PHP, Perl, Scheme, Haskell, Standard ML,
Clipper, Basic, Visual Basic, Java, JavaScript, SQL, Late,x Postscript,
HTML, UML, Z, Act-One, VDM, awk, LEX, YACC, Maschinensprachen,
RPG, Occam, Linda, T Lotus, OPS-5, ...
 werden Sie zu Meta-Programmierern und -Programiererinnen
Lösung 7.2
Reguläre Ausdrücke
1. Geben Sie reguläre Ausdrücke für
a) Integerliterale:
b) while, function, if
[0-9]+ bzw. (1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)*
while usw. bzw. ‘w‘‘h‘‘i‘‘l‘‘e‘ usw.
2. Geben Sie einen regulären Ausdruck zu folgenden Sprachen an:
a) Alle Folgen von Großbuchstaben, die jeden Vokal genau einmal in
alphabetischer Reihenfolge enthält:
KONS = [B-DF-HJ-NP-TV-Z]
{KONS}*A{KONS}*E{KONS}*I{KONS}*O{KONS}*U{KONS}*
b) Alle Dualziffernfolgen, die „001“ nicht als Teilfolge enthalten
(0?1+)*0*
2. Welche Sprachen sind durch die folgenden regulären Ausdrücke
definiert ?
a) (0?|1*)*
b) (0|1)*0(0|1)(0|1)
c) /\*((\*[^/])|[^\*])*\*/
alle Binärzahlen, denn (0|1) ist Teilmenge von (0?|1*)
alle Binärzahlfolgen, bei denen die drittletzte Ziffer
existiert und 0 ist
„wohlgeformte“ C-Kommentare
Lösung 7.3
Grammatiken
1. gegeben ist folgende Grammatik G:
G = { N,T,P,S }, N = { A,B,C,S }, T = { a,b,c },
P = { S:=ABC, A:=ABA, C:=CBC, A:=a, B:=b, C:=c }
a) Die Grammatik ist kontextfrei, da auf der linken Seite aller Regeln genau
ein Nichtterminalsymbol steht
b) Beweis durch Ableitung :
S  ABC  ABA BC  ABA BABC  ABABAB CBC  ... :
abababcbc
c) Es gibt keine Regel, die ein b vor ein a produziert, ohne dass vor dem b
auch noch a‘s sind, daher ist b2a2c3  L(G), denn in b2a2c3 ist ein b vor
einem a.
d) (ab)+c(bc)*
e) Da die Grammatik G kontextfrei ist die Sprache vom Chomsky-Typ-2. Da
sich die Sprache auch als regulären Ausdruck darstellen lässt, ist die
Sprache sogar Chomsky-Typ 3.
f) Ja, denn jede Chomsky-Typ2 bzw. 3 Sprache ist auch vom Chomsky-Typ0