0 - EvIM - ETH Zürich
Werbung
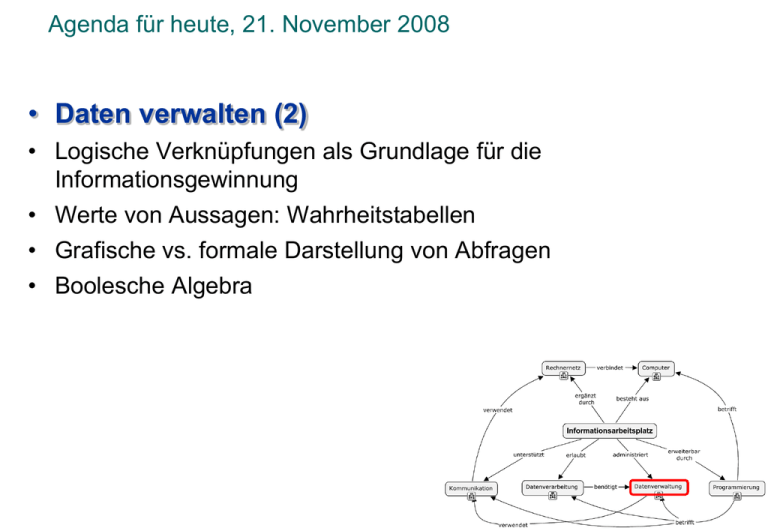
Agenda für heute, 21. November 2008 • Daten verwalten (2) • Logische Verknüpfungen als Grundlage für die Informationsgewinnung • Werte von Aussagen: Wahrheitstabellen • Grafische vs. formale Darstellung von Abfragen • Boolesche Algebra Daten verwalten (2): Drei Stufen der Datenverwaltung Anwendung Informatik • Daten organisieren • Entity-Relationship-Modell • Daten speichern • Datenbanken • Daten wieder gewinnen • Abfragen (z.B. mit SQL) • Daten reorganisieren • Logische Verknüpfungen • Daten austauschen • Datenformate • Daten umformen • Standards 2/25 © Departement Informatik, ETH Zürich Daten organisieren, Daten speichern: Relationale Datenbank Ursprüngliche Information Normalisieren Relationen Relationale Operatoren (Select, Project, Join) Umstrukturierte Information 3/25 © Departement Informatik, ETH Zürich • Daten verwalten (2) • Logische Verknüpfungen als Grundlage für die Informationsgewinnung • Werte von Aussagen: Wahrheitstabellen • Grafische vs. formale Darstellung von Abfragen • Boolesche Algebra Wiedergewinnen von Information: Aussagenlogik Welche Nahrungsmittel enthalten weniger als 2 mg Eisen? Datenbankabfrage Name in Nahrungsmittel mit Nährstoff = Eisen und Menge < 2 Aussage ausgewertet mit Tupel einer Datenbank wahr falsch (z.B. 1.7mg Eisen) (z.B. 3.4mg Eisen) 4/25 © Departement Informatik, ETH Zürich Elemente der Aussagenlogik • Eine Aussage hat einen Wahrheitswert ("wahr", "falsch") • Aussagen können aus Teilaussagen zusammengesetzt sein • Diese Teilaussagen sind durch logische Operatoren verknüpft Der Wahrheitswert einer zusammengesetzten Aussage ist vollständig durch die Wahrheitswerte der Teilaussagen und die Art der Verknüpfung gegeben. 5/25 © Departement Informatik, ETH Zürich Logische Operatoren Die logischen Operanden p und q sollen Teilaussagen bezeichnen z.B. p steht für: Nährstoff = Eisen q steht für: Menge < 2 (kann wahr sein oder falsch) (kann wahr sein oder falsch) • Konjunktion: "sowohl p als auch q" p and q • Disjunktion: "entweder p oder q" p or q • Negation: "nicht p" not p 6/25 © Departement Informatik, ETH Zürich • Daten verwalten (2) • Logische Verknüpfungen als Grundlage für die Informationsgewinnung • Werte von Aussagen: Wahrheitstabellen • Grafische vs. formale Darstellung von Abfragen • Boolesche Algebra Werte von Aussagen: Wahrheitstabellen • Logische Verknüpfungen anschaulich spezifizieren • Für jede mögliche Kombination von logischen Operanden wird das Resultat der Verküpfung aufgelistet p q Verknüpfung von p mit q w w x w f x f w x f f x w = wahr, f = falsch 7/25 © Departement Informatik, ETH Zürich Wahrheitstabelle für die Konjunktion Symbole: und, and, •, p q p and q w w w w f f f w f f f f Die erste Zeile ist eine Kurzform für: "Falls p wahr ist und q wahr ist, dann ist p and q wahr Für alle Zeilen: wenn p dann q sonst falsch 8/25 © Departement Informatik, ETH Zürich Wahrheitstabelle für die Disjunktion Symbole: oder, or, +, p q p or q w w w w f w f w w f f f Beachte: p or q ist nur dann falsch wenn beide Teilaussagen falsch sind Für alle: wenn p dann wahr sonst q 9/25 © Departement Informatik, ETH Zürich Beispiele Rosen sind rot and Veilchen sind blau ist wahr wahr and wahr Rosen sind rot and Veilchen sind grün ist falsch wahr and falsch Rosen sind rot or Veilchen sind blau ist wahr wahr or wahr Rosen sind rot or Veilchen sind grün wahr or falsch ist wahr Rosen sind silbrig or Veilchen sind grün ist falsch 10/25 falsch or falsch © Departement Informatik, ETH Zürich Wahrheitstabelle für die Negation Symbole: nicht, not, ¬ p not p w f f w Vorrangregelung der logischen Operatoren : 1. not 2. and p or q and r 3. or 4. Vergleiche Kann durch Setzen von Klammern aufgehoben werden ≠ (p or q) and r 11/25 © Departement Informatik, ETH Zürich Bemerkungen zur Disjunktion Umgangssprachlich bedeutet "oder" meistens: p oder q oder beide (sie ist intelligent oder sie studiert jede Nacht) p or q bedeutet immer "p oder q oder beide" (siehe Wahrheitstabelle) manchmal bedeutet "oder" jedoch: p oder q aber nicht beide (sie telefoniert aus Basel oder aus Genf) für diese Bedeutung wird die exklusive Disjunktion (xor) angewandt p q p xor q w w f w f w f w w f f f Beachte: p xor q ist dann falsch wenn beide Teilaussagen entweder falsch oder richtig sind. 12/25 © Departement Informatik, ETH Zürich Disjunktion oder exklusive Disjunktion? Genauer: drink xor drive Aber stimmt das? Genauer: drink and < 1 Glas xor drive Stimmts jetzt? Genauer: (drink and ≤ 1 Glas and drive) or (drink and > 1 Glas and not drive) 13/25 © Departement Informatik, ETH Zürich Das neue Plakat © Raphael Theiler 14/25 © Departement Informatik, ETH Zürich Ein paar Spezialfälle Logische Äquivalenzen not p or not q not ( p and q ) not p and not q not ( p or q ) (de Morgan) Tautologie Widerspruch p or not p p and not p p not p p or not p p not p p and not p w f w w f f f w w f w f 15/25 © Departement Informatik, ETH Zürich • Daten verwalten (2) • Logische Verknüpfungen als Grundlage für die Informationsgewinnung • Werete von Aussagen: Wahrheitstabellen • Grafische vs. formale Darstellung von Abfragen • Boolesche Algebra Grafische vs. formale Darstellung logischer Verknüpfungen Welche Nahrungsmittel enthalten weniger als 2 mg Eisen oder Zink? Mengendiagramme Alle Nahrungsmittel mit Zink Alle Nahrungsmittel mit Eisen Alle Nahrungsmittel mit Menge < 2 mg Logischer Ausdruck (Menge < 2 mg) and (Nährstoff = Eisen) or (Nährstoff = Zink) 16/25 © Departement Informatik, ETH Zürich Grafische vs. formale Darstellung logischer Verknüpfungen (Menge < 2 mg) and (Nährstoff = Eisen) or (Nährstoff = Zink) Menge and Eisen Eisen Zink Menge 17/25 © Departement Informatik, ETH Zürich Grafische vs. formale Darstellung logischer Verknüpfungen Welche Nahrungsmittel enthalten weniger als 2 mg Eisen oder weniger als 2 mg Zink? Logischer Ausdruck (Nährstoff = Eisen) and (Menge < 2 mg) or (Nährstoff = Zink) and (Menge < 2 mg) 18/25 © Departement Informatik, ETH Zürich Wahrheitstabellen für die Analyse logischer Ausdrücke (Menge < 2 mg) and (( Nährstoff = Eisen) or (Nährstoff = Zink)) < 2 mg Eisen Zink Eisen or Zink (Eisen or Zink) and < 2 mg W W W W W W W F W W W F W W W W F F F F F W W W F F W F W F F F W W F F F F F F 19/25 © Departement Informatik, ETH Zürich Wahrheitstabellen für die Analyse logischer Ausdrücke (Menge < 2 mg) and ( Nährstoff = Eisen) or (Nährstoff = Zink) < 2 mg Eisen Zink < 2 mg and Eisen < 2 mg and Eisen or Zink W W W W W W W F W W W F W F W W F F F F F W W F W F W F F F F F W F W F F F F F 20/25 © Departement Informatik, ETH Zürich • • • • Daten verwalten (2) Logische Verknüpfungen als Grundlage für die Informationsgewinnung Werte von Aussagen: Wahrheitstabellen Grafische vs. formale Darstellung von Abfragen • Boolesche Algebra Boolesche Algebra Eine Menge M mit zwei Verknüpfungen "•" und "+" heisst Boolesche* Algebra, wenn für alle x, y, z M gilt: (1) x • (y • z) = (x • y) • z; Assoziativ (2) x + (y + z) = (x + y) + z; Assoziativ (3) x • y = y • x; Kommutativ (4) x + y = y + x; Kommutativ (5) x • (x + y) = x; Absorption (6) x + (x • y) = x; Absorption (8) x • (y + z) = (x • y) + (x • z); Distributiv (8) x + (y • z) = (x + y) • (x + z); Distributiv * nach George Boole, englischer Mathematiker, 1815 – 1864 21/25 © Departement Informatik, ETH Zürich Boolesche Algebra (9) es gibt ein Element 0 M mit 0 • x = 0 und 0 + x = x für alle x M ; Neutrales Element (10) es gibt ein Element 1 M mit 1 • x = x und 1 + x = x für alle x M ; Neutrales Element (11) zu jedem x M existiert genau ein y M mit x • y = 0 und x + y = 1; Komplementäres Element Wir ersetzen "wahr" mit "1" und "falsch" mit "0" und wenden die Boolesche Algebra auf logische Ausdrücke an. 22/25 © Departement Informatik, ETH Zürich Vereinfachung logischer Ausdrücke Wir möchten einen Fruchtsalat mit Ananas und Bananen oder mit Ananas und keinen Bananen oder mit keinen Ananas und keinen Bananen. Können wir das einfacher sagen? Was sagen wir überhaupt? Ananas und Banane oder Ananas und keine Banane oder keine Ananas und keine Banane 23/25 © Departement Informatik, ETH Zürich Vereinfachung logischer Ausdrücke Ananas und Banane oder Ananas und keine Banane oder keine Ananas und keine Banane 1. 2. 3. 4. 5. 6. 7. (A • B) + (A • ¬B) + (¬A • ¬B) [A • (B + ¬B)] + (¬A • ¬B) (A • 1) + (¬A • ¬B) A + (¬A • ¬B) (A + ¬A) • (A + ¬B) 1 • (A + ¬B) A + ¬B Distributivgesetz komplementäres Element bez. + neutrales Element bez. • Distributivgesetz komplementäres Element bez. + neutrales Element bez. • Ananas oder keine Banane Aber . . . sind der 1. und der 7. Ausdruck auch äquivalent? 24/25 © Departement Informatik, ETH Zürich Verifizierung logischer Ausdrücke 1. Ausdruck: A B ((A • B) + (A • ¬B)) + (¬A • ¬B) 1 1 1 1 1 1 1 0 0 1 0 0 0 1 0 1 0 0 1 1 1 1 1 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 Schritt: 1 2 1 5 1 3 1 6 1 4 1 7. Ausdruck: Reihenfolge: 1. Aussage 2. Logischer Ausdruck (Symbole) 3. Boolesche Algebra 4. Ausdruck evaluieren 25/25 A B A + ¬B 1 1 1 1 0 1 0 1 1 1 0 1 0 0 0 0 0 0 1 1 Schritt: 1 2 1 © Departement Informatik, ETH Zürich Wir wünschen Ihnen ein schönes Wochenende