Begriffe

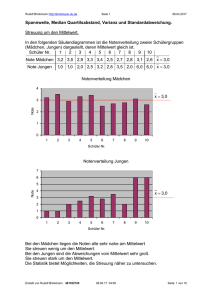
Referat über das Thema
STOCHASTIK
Themen

Begriffe

Statistik

Streuungsparameter

Varianz und Standardabweichung

Baumdiagramm

Laplace Wahrscheinlichkeiten
Begriffe

Ergebnisraum Ω
Die Menge aller mögichen Ergebnisse eines Zufallsexperiments

Ereignis E
Das Auftreten von Ergebnissen

Ereignisraum
Menge aller möglichen Ereignisse, d. h. aller Teilmengen von Ω

Mächtigkeit der Menge |E|
|E| gibt die Anzahl der Elemente an die in E liegen

Median (Zentralwert)
Der Wert für den jede Hälfte der Stichprobe höhere bzw. niedrigere Messwerte aufzeigt

Spannweite
Die Differenz zwischen dem kleinsten und dem größten Messwert

Modalwert
Der Wert, der bei der Stichprobe am häufigsten auftaucht
Statistik
Def.: Die beschreibende Statistik befasst sich mit der
Untersuchung von abgegrenzten Grundgesamtheiten
hinsichtlich eines Merkmals. Die Erfassung der
Merkmalsausprägungen und deren Aufbereitung lassen so
Schlussfolgerungen zu.
Begriffe:
Qualitative Merkmale
Quantitative Merkmale
Beziehen sich auf Eigenschaften
wie gut, schlecht, Familienstand,
weiblich, männlich, usw.
Lassen sich durch Zahlen angeben
wie Alter, Gewicht, Geldbetrag,
usw.
Sport
Fußball
Eishockey
Golf
Tennis
Anzahl
12
8
2
10
Häufik in %
12/32 *100= 37,5% 25%
6,25%
31,25%
h=f/n
Def.: Die absolute Häufigk. (f) ist die
konkrete Anzahl eines Merkmals.
Def.: Die relative Häufigk. (h) ist der
Anteil vom Ganzen [%].
Fußball
Eishockey
Tennis
Streuungsparameter

1.Spannweite
Def.: Ein einfaches Maß für die Streuung um den Mittelwert ist die
Differenz der zwischen der größten und den kleinsten Wert
der Reihe – Die Spannweite

2. Mittlere lineare Abweichung
Def.: Ist die Darstellung der Abweichung vom Mittelwert
Formel: |x -M| + |x -M| + … + |x -M|
1
2
n
n
Varianz und Standardabweichung
Hoch 2
Erreichte Punktzahl
Differenz zum
Mittelwert
Quadrat der
Differenzen
17
3,7
13,69
8
5,3
28,09
9
4,3
18,49
1,32
1,69
10
3,30
10,89
21
7,7
59,29
16
2,7
7,29
12
Mittelwert
13,3
Varianz:
Wurzel nehmen
139,43
Standardabweichung: 11,81
Baumdiagramm
Beispiel: Urne
Rechnung:
rot / rot => 3/5 * 2/4 = 0,3 => 30 %
rot / grün => 3/5 * 2/4 = 0,3 => 30 %
grün / rot => 2/5 * 3/4 = 0,3 => 30 %
grün / grün => 3/5 * 1/4 = 0,1 => 10 %
Laplace Wahrscheinlichkeit
m = Elemente des Ereignisses
n = Elemente der Ergebnismenge
Die Wahrscheinlichkeit P(E) wird immer angegeben zwischen 0 und 1.
0 = keine Chance für das Eintreten
1 = E tritt sicher ein
Das war das Referat über
die Stochastik
Pierre - Simon Laplace ( 1749 – 1827 )
war ein französischer Mathematiker.
Er beschäftigte sich unter anderem
mit der Wahrscheinlichkeitstheorie
und Differentialgleichungen.