bei q

Qualitative
Charakterisierung von
Verteilungen.
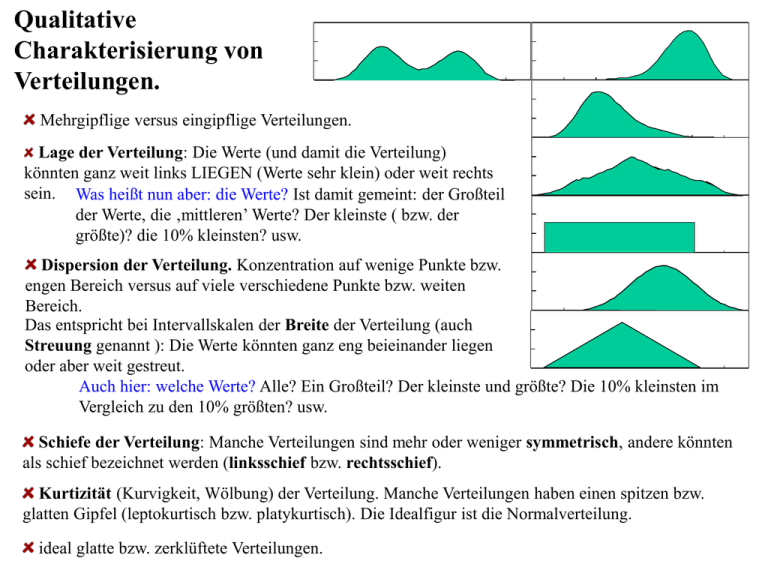
Mehrgipflige versus eingipflige Verteilungen.
Lage der Verteilung: Die Werte (und damit die Verteilung)
könnten ganz weit links LIEGEN (Werte sehr klein) oder weit rechts
sein. Was heißt nun aber: die Werte? Ist damit gemeint: der Großteil
der Werte, die ‚mittleren’ Werte? Der kleinste ( bzw. der
größte)? die 10% kleinsten? usw.
Dispersion der Verteilung. Konzentration auf wenige Punkte bzw.
engen Bereich versus auf viele verschiedene Punkte bzw. weiten
Bereich.
Das entspricht bei Intervallskalen der Breite der Verteilung (auch
Streuung genannt ): Die Werte könnten ganz eng beieinander liegen
oder aber weit gestreut.
Auch hier: welche Werte? Alle? Ein Großteil? Der kleinste und größte? Die 10% kleinsten im
Vergleich zu den 10% größten? usw.
Schiefe der Verteilung: Manche Verteilungen sind mehr oder weniger symmetrisch, andere könnten
als schief bezeichnet werden (linksschief bzw. rechtsschief).
Kurtizität (Kurvigkeit, Wölbung) der Verteilung. Manche Verteilungen haben einen spitzen bzw.
glatten Gipfel (leptokurtisch bzw. platykurtisch). Die Idealfigur ist die Normalverteilung.
ideal glatte bzw. zerklüftete Verteilungen.
Quantitative Charakterisierung, Lage: Min, Max, Mode
Sortierte Liste
Lagemaßzahl
Beispiele:
Minimum bzw.
Maximum
min(x)= x(1), max(x)= x(n).
Mit x(1) und x(n) aus der
sortierten Liste
Modalwert (engl.
Mode): mode(x)
Der Modalwert ist der
x-Wert mit größter
Dichte.
min(Alter) = 21 = x(1)
max(Alter) = 30 = x(16)
mode(Alter)= 21. Denn f(x) ist
bei 21 am größten
Für den Modalwert gilt:
f(mode(x)) = max (f(x))
x
mode(Familienstand) = 0
(=ledig). Denn f(x) ist bei
‚ledig‘ am größten: 11/16.
mode(IQ) = 100. Denn f(x) ist
bei 100 am größten.
Problem: Es kann
Dichtefunktion
f(x),auch
x=AlterZwei Lösungsstrategien:
Streifendiagramm,
vertikal
Anteil
f(x)
mehrere Modalwerte
Modalwertmenge
berichten.
0.8
0.00100
0.4geben
(bimodale oder
Eindeutigkeitsstrategie:
0.00090
 Bei Intervallen das
0.00080
0.6 multimodale
0.3sogar
0.03
0.00070
Intervallmittel berechnen.
Verteilungen)
f(IQ)
0.00060
 Sonst: Modalwert nur für
0.2 0.4
f(x)
0.02
0.00050
unimodale Verteilungen als
sinnvoll.
0.01
0.2
0.10.00040
0.00030
0
0.00020
50
0 0.00010
18
0
0
0
70
90
110
130
20
22verlobt
24 IQ
ledig
Normalverteilung
für den
1000
2000
3000
IQ
150
26
28
getrennt
4000
30
5000
x
mode(Einkommen) = Intervall
von 0 bis 100.
bzw.
mode(Einkommen) =
Intervallmittel = 50
Index
(i)
Wert
x(i)
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
21
21
21
21
21
21
22
22
22
22
23
23
24
24
24
30
Quantitative Charakterisierung, Lage: Median und Co.
Lagemaßzahl
Median (‚mittlerer Wert‘): med(x)
ist der x-Wert, der die Verteilung in
zwei Hälften teilt.
0.03
Für diskrete Verteilungen präziser:
med(x) ist der x-Wert, für den die
beiden Forderungen gelten:
1. mindestens die Hälfte aller
Werte ist kleiner gleich med(x)
2. mindestens die Hälfte aller
Werte ist größer gleich med(x)
0
50
0.4
Der Median med(x) ist hier = 100.
f(x)
0.02
Anteilsverteilung
0.01
0.3
Index
70
90
110
130
x 150
f(x)
0.2
0.1
0
18
20
22
24
26
28
30
x
Anteil
Wert
i
xi
p(xi)
1
2
3
4
5
21
22
23
24
30
0.375
0.125 + 0.125
0.125
0.1875
0.0625
Der Median med(x) ist hier = 22
Diese Idee kann auch auf andere Quantelungen ausgedehnt werden: Einteilung
in 3 Teile, 4 Teile usw.
Terzile sind die beiden x-Werte, die die Verteilung in drei Drittel teilt: 1. Terzil und 2. Terzil.
Quartile sind die 3 x-Werte, die die Verteilung in 4 Viertel teilt: 1. Quartil und 2. Quartil (= Median) und 3. Quartil.
Darüber hinaus gibt es: Quintile (5 Teile), Sextile (6 Teile), Septile (7 Teile), Oktile (8 Teile), Dezile (10 Teile) usw.
Perzentile heißen die 99 Werte, die eine Quantelung in 100 Teile ermöglichen: 1. Perzentil, 2. Perzentil usw.
Quantile: Diese ‚-ile‘ können unter
dem Begriff Quantil zu bestimmten
Quanten (= q) zusammengefasst
werden.
Beispiel: Das 1. Terzil ist das Quantil zum Quantum 1/3. Das 2. Terzil ist das Quantil
zum Quantum 2/3.
Beispiel: Das 1. Quartil ist das Quantil zum Quantum 1/4. Das 3. Quartil ist das
Quantil zum Quantum 3/4.
Quantile
0.03
f(x)
0.4
Bis zu welchem x-Wert
0.01
liegt ein gegebenes
0
50
70
90
110
130 x 150
Quantum q (=Anteil)
Dieser x-Wert heißt Quantil zum Quantum q:
aller Werte?
0.2
0.02
0.3
f(x)
0.1
0
~
xq
18
20
22
24
26
x
¾Sortierte Liste
Bei diskreten Verteilungen
Auf Grund der sortierten Liste
das Quantil berechnen:
30
Quantile zu
q=
Für diskrete Verteilungen
muss diese Definition
präzisiert werden: für ~
xq
gelten die beiden
Forderungen:
1. mindestens q aller Werte
ist kleiner gleich ~
xq ,
2. mindestens (1-q) aller
~
Werte ist größer gleich x q .
28
Index
Gesucht: ~
x1 3 . Das Quantum q=1/3,
n=16. z:=16*(1/3) = 5.3333.
z ist keine ganze Zahl; daher muss
[z]+1 berechnet werden: [5.3333]+1
= 6. Das Quantil ~
x1 3 ist daher
das 6. aus der sortierten Liste: x(6)
= 21.
Wert
Sortierte
Liste
(i)
x
(i)
Index Wert
(1)
21
(i)
x(i)
(2)
21
Berechne z:= n*q
(1)
21
(3)
(2)
(4) der21
Problem
Ist z eine
nein
(3)
21
(5)
Nichteindeutigkeit
ganze Zahl?
~
(6)
Quantils21wird
Gesucht: x 3 4. Das Quantum q= ¾, des(4)
~
x q := x ([ z ]+1)
n=16. z:=16*(¾) = 12.
21
nur(5)
durch die
(7)
22
ja
z ist eine ganze Zahl. Daher ist das
Konvention
der
(6)
21
(8)
22
~
x
x
+
(
)
(
)
z
z +1
Quantil x 3 4 =: (x(12) + x(13) )/2 = Mittelwertbildung
~
(7)
22
(9)
x q :=
2
(23+24)/2 = 23.5.
gelöst.
(8)
22
(10)
22
[z] Die
Klammern ummit
die Zahl z bedeuten, dass die Dezimalstellen abgeschnitten
werden sollen
Verteilungsfunktion
für(diese
Alter(9)
(11)
23
Die eckigen
beiden Forderungen,
So kann das Quantil auch mit Hilfe
1.0
Dezimalstellenabschneideregel
auch Floor-Function).

(10)
22
(12)
23
der Verteilungs- und Dichte-heißtder
Verteilungsfunktion graphisch
0.9
F(x)
(11)
23
(13)
24
0.8
funktion
formuliert,
lauten: = 2,bestimmt
werden:
Beispiele:
[5.13]
= 5, [2.4711]
[0.61543]
=0

q=¾
0.7
(12)
23
(14)
24

q  F( ~
x q ) und
Starten von der Ordinate bei q.
0.6
(13)
24
(15)
q = 0.5
~
~
F( x q )  f ( x q )  q
An der Stelle, wo man auf die
(14)
24
(16)
30
0.4

q
=
1/3
Funktion F(x) stößt, ist auf der
(15)
24
0.3
~
d.h. x q liegt dort auf der xx-Achse (Abszisse) das Quantil
0.2
(16)
30
Achse, wo F(x) erstmals q
zum Quantum q ablesbar.
0.1
0.0
überschreitet bzw. erreicht.
18
20
22
24
26
28
30
Quantile bei stetigen Verteilungen
Für stetige Verteilungen
können Quantile einfacher
definiert werden als für die
diskreten.
~
x q ist der x-Wert, für den gilt:
q = F( ~
x q) .
Graphisches Verfahren:
Starten von der Ordinate bei q.
An der Stelle, wo man auf die
Funktion F(x) stößt, ist auf der
x-Achse (Abszisse) das Quantil
zum Quantum q ablesbar.
1.0
0.9
q = 0.80 0.8
0.7
0.6
q = ½ 0.5
0.4
0.3
q = ¼ 0.2
0.1
0.0
F(x)
1000
0
Berechnen für gruppierte
Daten
Die in Klassen gruppierten
Messwerte seien pro Klasse
gleichverteilt im Intervall
[ui,oi). Zudem sei der
kumulierte Anteil in jeder
Klasse F(oi) bekannt.
Dann kann das Quantil wie
folgt berechnet werden.
In der Anteilsverteilung den
Index m finden, für den F(om)
erstmals q überschreitet (F(om)
> q) bzw. erreicht (F(om) = q).
F(om)
>q
o
u
~
x q := m + m +1
(q  F(u m ))b m
~
x q:= u m +

2000 ~ 3000
xq
5000
x
4000
Gesucht: x0.7 , daher ist q = 0.7. Index m = 4. Hier erreicht
F(o4) nun 0.7; F(o4) = 0.7. o4= 2000. u5=2000. Daher ist
~
das Quantil x0.7 = (2000 + 2000)/2 = 2000.
~
Gesucht: x.8 , daher ist q = 0.80. Index m = 5. Erst hier ist
F(o5) > 0.80. u5= 2000. F(u5) = F(2000) = 0.70. Daher ist
~
das Quantil x.8 = 2000 + (0.80-0.70)3000/ 0.30 = 3000.
Gesucht: x½ , daher ist q = 0.50. Index m = 4. Erst hier ist
F(o4) > 0.50. u4= 1000. F(u4) = F(1000) = 0.40. Daher ist
~
der Median x½ = 1000 + (0.50-0.40)1000/ 0.30 = 1333.3.
~
Gesucht: x¼ , daher ist q = 0.25. Index m = 3. Erst hier ist
F(o3) > 0.25. u3= 500. F(u3) = F(500) = 0.20. Daher ist das
~
1. Quartil x¼ = 500 + (0.25-0.20)500/ 0.20 = 625.
Jeder Klasse entspricht eine Gerade.
Kumulierte
Anteilsverteilung
Für q muss festgestellt werden, welche
Gerade benötigt
wird.
Die Geradengleichung allgemeinKlassen
ist: y = a +Klassen
bx. Die Gerade
geht durch
die
Klassen
Kum.
Punkte (u m, F(u m) ) und (o m, F(o mIndex
)) .
Breite
Anteil
Grenzen
F( o m ) F( u m ) F(o )
a und b kann durch Einsetzen der Punkte
b bu m
i
o
=
bu=
i
o m iu m , a i F(u m ) i
in die Gleichung berechnet werden.
100
1
0
100
0.10
~
= a + b500
q
xq  ~
x0.20
/b
Nun wird der Punkt (~
xq , q) in die 2
q = (q  a )400
100
1
~
 F(u m ) +0.40
Gleichung eingesetzt.
3
x500
bu m ) b 500
q = (q 1000
F(x)
1000
4000
~
=q
2
Begründung der Formel für das Quantil
0
3000
~
F(o m ) F(u m )
1.0
0.9
q = 0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.0
2000
625 1333
5000
x
Weiteres Umformen und Einsetzen
von a und b liefert die Formel:
4
5
1000
2000
0.70
1000
om u m
~
= u m +5000
x q2000
(q  F(u 1.00
m )) F( u m ) 3000
F( u m )
Median, Hinges und Eighths aus
der EDA.
In der EDA (TUKEY, 1977 Exploratory Data Analysis) wurden
innovativ ‚anschauliche‘ Begriffe und Konzepte eingeführt, die denen
der ‚klassischen‘ Statistik ähnlich sind, aber etwas anders definiert sind.
So entsprechen die ‚Hinges‘ (=Falten) fast dem 1. und 3. Quartil, die
‚Eighths‘ fast dem 1. und 7. Oktil, aber nicht bei jedem n.
Berechnungsmethode
Zuerst wird die Tiefe für die Größen berechnet; das ist die Position in
der sortierten Liste von vorne bzw. von hinten.
Tiefe(Median)=(n+1)/2.
Tiefe(Hinges)=([Tiefe(Median)]+1)/2.
Tiefe(Eighths)=([Tiefe(Hinges)]+1)/2.
Beispiel: 9 sortierte Werte 7, 18, 23, 24, 25 ... . Man denke sich die UEen als
Perlen, die auf eine Schnur aufgezogen sind.
Hält man die Schnur an beiden Enden fest, fällt die Schnur so, dass unten die
Medianperle hängt. Der Median ist dann 25.
1
7
1
29
5
25
4
24
2
18
4
26
2
28
5
3
3
hu Hinges
ho
25
27
23
Durch Hochziehen der Medianperle entstehen Falten, bei der 3. Perle (von vorn
bzw. hinten): die beiden Werte 234und 27 sind die4Hinges
24
26
5
Beispiel: 10 Werte, zusätzlich 32. Hochziehen
in der Mitte.
25
5
5
25
26
Mittel der beiden:
4 25.5
4
5 = Median
5
24
27
25
26
1
7
Der Median(x) = x(Tiefe(Median)) , falls Tiefe(Median) eine ganze
Zahl ist, sonst ist der Median das Mittel der beiden Werte, zwischen
denen die Dezimalzahl liegt.
2
18
3
23
Entsprechend erfolgt die Berechnung der beiden Hinges (hu, ho) und
der beiden Eighths(eu, eo).
4
24 hu 5Hinges5
25
26
4
ho 27
1
32
2
29
3
28
4
4 Hochziehen der Medianperle.
Beispiel: 11 Werte, zusätzlich 38.
27
24
Beispiel (9 Werte). Tiefe(Median)=(9+1)/2 = 5. Tiefe(Hinges)=([5]+1)/2 = 3.
Tiefe(Eighths)=([3]+1)/2 = 2.
Median(x) = 25. hu = 23 (3. von vorne), ho = 27 (3. von hinten), eu = 18 (2. von
vorne), eo = 28 (2. von hinten).
Beispiel (10 Werte). Tiefe(Median)=(10+1)/2 = 5.5. Tiefe(Hinges)=([5.5]+1)/2 = 3.
Tiefe(Eighths)=([3]+1)/2 = 2.
Median(x) = (25+26)/2. hu = 23 (3. von vorne), ho = 28 (3. von hinten), eu = 18 (2.
von vorne), eo = 29 (2. von hinten).
Beispiel (11 Werte). Tiefe(Median)=(11+1)/2 = 6. Tiefe(Hinges)=([6]+1)/2 = 3.5.
Tiefe(Eighths)=([3.5]+1)/2 = (3+1)/2 = 2.
Median(x) = 26. hu = 23.5 (Mittel des 3. und 4. von vorne), ho = 28.5 (Mittel des 3.
und 4. von hinten), eu = 18 (2. von vorne), eo = 32 (2. von hinten).
5 6 5
25 26 26
1
7
2
18
5
25
4
3
5
24
23
25
Mittel der beiden:
23.5 4
hu
24
5
6
26
1
38
5
27
2
32
4
3
28
29
Mittel der beiden:
4 28.5
ho 28
5
27
6
Hinges
26
5
Der Prozess des Faltens könnte
werden, indem
25 weiter fortgesetzt
27
die Hinges selbst hochgezogen werden.
Das führt dann zu einer Art
6
Achtelung der Perlenkette. Usw. 26
Lagemaß Arithmetisches Mittel x
Das arithmetische Mittel
(engl. Mean) wird auch als
Mittel, Durchschnitt oder
Schwerpunkt (engl.
Centroid) bezeichnet bzw.
etwas unpräzis einfach als
der Mittelwert.
Für Urliste:
+ + ... + x n 1 n
x = x1 x 2
=  xi
n
n i =1
Die Schwerpunkt-Eigenschaft
bedeutet, dass die Summe der
Differenzen zum Mittel 0 ist,
was auch mit Hilfe einer
Dezimalwaage demonstriert
werden kann.
Die Summe der Differenzen zum
Mittelwert ist 0:
Für Verteilung:
x =
I

i =1
pi x i =
I
1
n
= n i x i
i 1
Arithmetisches Mittel des Alters (aus Urliste)
x = (22+24+...+23+21+21) / 16 = 362 / 16 = 22.625.
n=16, es wird über 16 Werte gemittelt (ungewichtet).
Arithmetisches Mittel des Alters (aus Verteilung) mit
Anteilen (I=5):
6
3
4
2
1
x = 16
21+ 16
22 + 16
23+ 16
24 + 16
30 = 22.625.
Mittel über 5 Werte (mit Anteilen als Gewichten).
21
22
23
( x1  x ) + ( x2  x ) + ...+ ( xn  x )
= nx  nx = 0
n x = x1 + x 2 + ... + x n
_
X
22.625
x ist translationsäquivariant
bei linearen Transformationen:
y = a + b x.
D. h.: Werden alle einzelnen
Werte linear transformiert, gilt
dies auch für das arithm. Mittel:
y = a + bx
Für jeden der n x-Werte werden die yWerte gebildet:
y i = a + bx. i
Den y-Mittelwert erhält man aus x
mit der gleichen Transformation.
Beweis:
y = ((a + bx1 ) + ...+ (a + bxn )) / n
= (na + b( x1 + ...+ xn )) / n
= a + bx
25
26
27
27
28
29
30
Der Waagebalken habe kein Eigengewicht
= x1 + x2 + ...+ xn  nx
Beachte:
24
Bei den Werten des Balken wird
pro UE ein Gewicht gehängt.
Balance ist beim Mittelwert als
Haltepunkt gegeben.
Beispiel(4 x-Werte 0, 1, 2, 3): x ist 1.5.
Alle Werte werden linear via y = 96 + 100 x (96 ist a,
100 ist b) transformiert: Die y-Werte sind 96, 196, 296,
396. Wie groß ist der Mittelwert?
Statt nochmals neu den Mittelwert zu berechnen, kann
der Mittelwert ebenfalls nach der Transformation
berechnet werden: 96 + 100*1.5 = 246.
Beispiel: Währungsumrechnungen sind lineare
Transformationen mit a=0. Ist der Mittelwert in einer
Währung bekannt, kann er direkt in eine andere
Währung umgerechnet werden (ohne Kenntnis der
Einzelwerte).
Entscheidungshilfe: Arithmetisches Mittel oder Median
Das Mindestskalenniveau für das arithmetische Mittel ist das Intervallskalenniveau, für den
Median reicht das Ordinalskalenniveau.
Das arithmetische Mittel reagiert sensibel auf extreme Messwerte (Ausreißer), nicht aber der Median.
Beispiel: 2 Einkommenslisten, unterscheiden sich in nur einem Wert
Ohne Großverdiener: 100, 100, 100, 100, 200
Mit Großverdiener: 100, 100, 100, 100, 1100
0
500
1000
Mittel
Median
120
100
300
100
Das arithm. Mittel eignet sich nicht als Indikator dafür, wie es den ‚meisten‘ Leuten geht.
Der Median reagiert sensibler auf interne Veränderungen als das arithmetische Mittel.
Beispiel: Zuerst haben 5 Leute das gleiche Vermögen, dann nimmt einer jedem 100 weg.
Vor Putsch: 200, 200, 200, 200, 200
Nach Putsch: 100, 100, 100, 100, 600
0
500
Das arithm. Mittel bemerkt den ‚Putsch‘ nicht, der Median schon.
1000
Mittel
Median
200
200
200
100
Arithmetisches Mittel (stetige Verteilung)
Spezialfall: Berechnen für gruppierte Daten
Für gruppierte Daten kann die
übliche Formel für den
Mittelwert verwendet werden
mit den Klassenmitten als xWerten.
Anteilsverteilung
o + ui
xi = i
2
Berechnen der
Klassenmitten:
Für Verteilung:
x =
I
 pi x i
=
i =1
I
 ni xi
1
n
i =1
Klassen
Grenzen
Klassen
Mitte Produkt
Klassen
Index
i
ui
oi
pi
xi
pi xi
1
2
3
4
5
0
100
500
1000
2000
100
500
1000
2000
5000
0.10
0.10
0.20
0.30
0.30
50
300
750
1500
3500
5
30
150
450
1050
Anteil
x =Arithmetisches Mittel des Einkommens = 1685
Allgemeiner Fall
0.03
Der Mittelwert ist im stetigen
Fall das Integral des
Produktes der x-Werte mit der
Dichtefunktion.
Arithmetisches
Mittel:
b
 xf ( x )dx
a
f(x)
x
0.01
0
50
f(x) ist die Dichtefunktion der
Verteilung für
x  ( a , b)
Erläuterung
0.02
60
70
80
90
100
110
120
130
140
150
120
130
140
150
0.03
0.02
Für eine Einteilung des Bereichs von a bis b in mehrere gleich breite (= x)
Intervalle seien jeweils die Klassenmitten die x-Werte aus dem Bereich x  (a, b) .
Das arithmetische Mittel kann dann nach der üblichen Formel berechnet werden:
f(x)
0.01
0
50
x x
60
70
80
90
100
110
0.03
Mittel =
 x p(x) =  x (f(x)  x )
x(a,b)
x(a,b)
Einteilung kann feiner
gemacht werden, bis x
mickrig klein ist: dx
b
 xf ( x )dx
a
0.02
0.01
0
50
Beispiel: Gleichverteilung f(x) = 1/(b-a), in x (a,b). Das unbestimmte Integral
hier
 x b1a dx =
1
ba
 xdx =
1 1
ba 2
x
2, das bestimmte
a x b 1a dx =
b
1 1
b a 2
 xf (x)dx
ist
(b  a ) = 12 (b+ a).
2
Der Mittelwert der Gleichverteilung ist daher die Mitte des Definitions-Intervalls.
2
f(x)
x
60
x
70
80
x
90
100
x
110
120
x
130
140
x
150
Beispiel: Normalverteilung. Das Integral für das
arithmetische Mittel ist immer der Symmetriepunkt. Im
vorliegenden Fall also: 100.
Andere Mittelwerte: q-getrimmtes und q-winsorisiertes Mittel
Diese Mittelwertbildungen soll die Anfälligkeit des arithmetischen Mittels für Ausreißer abschwächen.
q ist der Anteil der fraglichen Ausreißer im oberen bzw. unteren Bereich und muss vorgängig festgelegt werden.
q-getrimmtes Mittel.
Beim getrimmten Mittel
wird ein Quantum q der
kleinsten Werte bzw.
größten Werte eliminiert.
Das arithm. Mittel der
restlichen Werte heißt das
q-getrimmte Mittel.
q-winsorisiertes Mittel.
Bei diesem Mittel wird
ein Quantum q der
kleinsten Werte bzw.
größten Werte durch
weniger extreme ersetzt.
Das arithm. Mittel der so
modifizierten Werte ist das
q-winsorisierte Mittel.
Für sortierte Liste:
Berechne z:= n*q.
Wähle die Werte
zwischen dem [z]. und
dem (n-[z]+1). aus:
x([z]+1) ,..., x(n-[z])
Berechne den Mittelwert
der ausgewählten Werte
Für sortierte Liste:
Wie oben z:= n*q.
Sortierte Liste
Beispiel: q-getrimmtes Mittel des
Alters für q=0.10. Bei n=16 ist z=1.6.
[z]= 1 (Dezimalstellen abgeschnitten).
Index
(i)
Wert
x(i)
Daher sollen die alle Werte zwischen
dem [z]. d.h. dem 1. und dem n-[z]+1.
d.h. dem 16-1+1. = 16.
Die Werte zwischen dem 1. und 16.
sind die Werte vom 2. bis zum 15.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
21
21
21
21
21
21
22
22
22
22
23
23
24
24
24
30
24
Der Mittelwert über die verbleibenden
Werte ist das q-getrimmte Mittel =
22.214
Beispiel: q-winsorisiertes Mittel des
Alters für q=0.10. Bei n=16 ist z=1.6.
[z]= 1 (Dezimalstellen abgeschnitten).
Ersetze den 1. bis zum
[z]. durch den [z]+1. Wert.
Der 1. bis 1. Wert soll durch den 2.
ersetzt werden.
Ersetze den (n-[z]+1). bis
zum n. durch den (n-[z]).
Die Werte vom 16. bis zum 16. Sollen
durch den 15. ersetzt werden.
Berechne den Mittelwert
dieser modifizierten Werte
Der Mittelwert über die modifizierten
Werte ist das q-winsorisierte Mittel =
22.25.
Quantitative Charakterisierung, Streuung
Streuungsmessung mit Hilfe der
EDA
Beispiel
Differenz zweier markanter Lagemaßzahlen
Streuungsmaßzahl
40
Beispiele:
sp(x) := Max(x) –Min(x)
Spannweite (engl. range)
:=Maximum-Minimum.
sp(Alter) = 30-21 = 9.
35
Sehr ‚sensibel‘ für einzelne Extremwerte.
Für manche Verteilungen unbrauchbar!
xq
d q := ~
x 1 q  ~
Quantilabstand
Differenz zwischen
symmetrischen Quantilen
für ein gegebenes Quantum q
e
Für q = 0.25 ist d. 0.25 der Quartilabstand;
für q = 0.10 ist d. 0.10 der Dezilabstand.
Für Alter: d 0.25 := ~
x0.75  x~0.25= 23.5 - 21= 2.5.
~
~
EDA-Beispiel
d 0.25 := x 0.75  x 0.25 = 29-23 = 6.
Der halbe Quantilabstand heißt mittlerer Quantilabstand.
H-Spread (Hingedifferenz)
E-Spread (Eighthsdifferenz)
dh := ho – hu
de := eo – eu
0.02
0.3
0.01
0.2
f(x)
110
89.9
110.1
~
x 0.25
82.7 h
e
130
~
x 0.75
h 117.3
e
150
0
e
15
10
0.1
90
h x~
20
EDA-Beispiel: hu=23.5. ho=28.5. eu= 18. eo= 32.
dh =5,
de =14
0.4
70
25
0.25
0.03
0
50
~30
h x 0.75
5
18
20
22
24
21
23.5
~
x
~
x
h
e
h
0.25
0.75
e
26
28
30
x
Alter
Quantitative Charakterisierung, Streuung
Streuungsmessung mit Hilfe der
Abweichungen aller Werte zu einer Lagemaßzahl Median
Streuungsmaßzahl
Beispiele:
0.4
Urliste:
Mittlere Abweichung
n
1
vom Median :=
d ~x 0.5 := n  | x i  ~x 0.5 |
i =1
arithmetisches Mittel
der Distanzen aller
Verteilung:
I
Werte zum Median.
~
d ~x 0.5 :=  p i | x i  x 0.5 |
i =1
Median-Abweichung Urliste:
MAD := Median (| x i  ~
vom Median :=
x 0.5 |)
i =1,L, n
Median der Distanzen
aller Werte zum
D.h. Erstellen einer sortierten
Liste der Abweichungen
Median.
vom Median.
engl. Median of
Für diese sortierte Liste
Absolute Deviations
den Median bestimmen.
= MAD.
0.3
f(x)
0.2
0.1
0
18
20
22
24
26
28
30
x
~
x½
d ~x0.5 = 166 | 21 22 | + 164 | 22  22 | + 162 | 23 22 | + 163 | 24  22 | + 161 | 30  22 |
6
3
4
2
1
= 16
1 + 16
0 + 16
1 + 16
2 + 16
8 = 1.375
Bei der Erstellung der sortierten Liste der Abweichungen vom
Median ist die Verteilung hilfreich, weil da schon gleiche
Werte zusammengefasst sind.
Erstellen einer sortierten Liste der Abweichungen vom
Median:
0, 0, 0, 0
1, 1, 1, 1, 1, 1,
2, 2, 2,
8.
4 Werte aus x=22.
4 Werte aus x=21, 2 Werte aus x=23
3 Werte aus x=24.
aus x=30.
~
x½
Für die sortierte Liste den Median bestimmen: Der Median
bei n=16 ist der Mittelwert des 8. und 9. Werts in der sortierten
Liste: (1+1)/2 = 1 = MAD.
Quantitative Charakterisierung, Streuung
Var(x) =
arithmetisches Mittel der
quadrierten Distanzen aller
Werte zum arithmetischen
Mittel der Werte.
Quadratsummen
Varianz:
Abweichungen aller Werte zum Lagemaß Arithm. Mittel
0.4
für Urliste:
n
sq x :=  ( x i  x ) 2
i =1
f(x)
0.2
0.1
0
für Verteilung:
18
20
22
24
26
28
30
x
I
sq x := n  p i ( x i  x ) 2
i =1
x =22.625
sq x = 16 (166 (21 22.625) 2 + 164 (22  22.625) 2 + 162 (23 22.625) 2
Standardabweichung: Varianz
Std(x) := Wurzel aus der
Varianz
0.3
_
Streuungsmessung mit Hilfe der
n  1
Var(x) :=  , n = 
n
 n
sq x
+ 163 (24  22.625) 2 + 161 (30  22.625) 2 )

Für n* = n-1:
Für n* = n :
= 77.75
Var(x) = 77.75 / 15  5.18
Var(x) = 77.75 / 16  4.86
Andere Bezeichnungen der Varianz Var(x)
Für die Stichprobe:
s 2 oder s 2x (um an das Merkmal zu erinnern) oder s 2n (falls durch n dividiert wird)
oder s 2n 1 (falls durch n-1 dividiert wird).
Für die Population:
 2 oder  2x (um an das Merkmal zu erinnern).
Wann und wozu durch n-1 dividieren?
Wann: Nur in Stichproben, wenn das arithmetische Mittel auch auf Grund der Stichprobe berechnet wurde. In allen
übrigen Fällen wird durch n dividiert.
Wozu: Die Division durch n-1 in Stichproben wird durchgeführt, wenn die Varianz der Population durch die Varianz
in der Stichprobe ‚erwartungstreu‘ geschätzt werden soll.
Bei Division durch n.
für Verteilung:
Var(x) := iI=1 p i (x i  x) 2
Bei Division durch n bzw. in diskreten
Populationsverteilungen kann die Varianz für die
Verteilung etwas einfacher formuliert werden.
Formeln zur Varianz
Varianz einer Linearkombination.
Alle x-Werte werden mit der
Linearkombination y = a + bx.
transformiert. Wie groß ist die
Varianz der transformierten Werte?
Varianz einer Linearkombination
Var(a+bx)= b2*Var(x)
Dehnung (um b) wirkt sich quadratisch im
quadratischen Konzept der Varianz aus.
‚Breite‘ bleibt gleich bei Verschiebung um a.
4-Väter-Beispiel: 4 x-Werte Alter: 42, 44, 46, 52
x = 46
Sei y= -21+ 0.5*x.
a= -21. b= 0.5.
y=2
xi
(xi  x )2
42
44
52
46
16
4
36
0
Verschiebungssatz für sqx
zur einfacheren Berechnung der
Quadratsummen bei
‚krummen‘ Mittelwerten:
n
n
sq x =  (x i  x )2 =  x i2  nx 2
i =1
i =1
Zuerst Summe der quadrierten Werte bilden. Erst danach den Mittelwert
(quadriert und mit n multipliziert) subtrahieren.
(yi  y )2
0
1
5
2
4
1
9
0
-21 + ½ x
•¼
Var(x) = 56 / 3
Verschiebungssatz.
yi
(½)2
Var(y) = 14 / 3
Beispiel: Alter, 16 Studenten. Mittelwert = 22.625.
Berechne zuerst Summe der quadrierten Werte:
2
2
2
2
6 * 21 + 4 * 22 + 2 * 23 + 3 * 24 + 30
2
= 8268
Danach
2
16*quadrierter Mw. berechnen 16 * 22.625 = 8190.25
Differenz: sqx = 8268 – 8190.25 =77.75 , wie vorher!
(Geschätzter) Standardfehler des arithmetischen Mittels
Der Standardfehler ist die Standardabweichung der Verteilung aller denkbaren
Mittelwerte, die man erhielte, wenn man etwa sehr viele Stichproben ziehen
würde (jeweils mit gleichem n).
Standardfehler des arithmetischen
Die Standardabweichung des arithm.
Mittels
1
Mittels ist kleiner als die der Werte
Stf ( x ) =
Std( x )
1
selbst, und zwar um den Faktor
.
n
n
Standardfehler des Altersmittelswerts bei einer
Stichprobengröße von n=16
Std( X ) = Std(x) / n = Std(x) / 4.
= 2.27668/ 4 = 0.56917
Etwas exakter spricht man vom geschätztem
Standardfehler, wenn die Std(x) selbst auf
Grund der Stichprobe geschätzt wird.
Geometrische Interpretation der Varianz
4-Väter-Beispiel: y-Werte 0, 1, 2, 5
y=2
Im ‚Variablen-Raum‘
Varianz als mittlere
Fläche
Die Werte werden zentriert (d.h. arithmetisches Mittel
wird subtrahiert) und auf dem Zahlenstrahl abgetragen.
Die Abweichungen
vom Mittelwert
werden quadriert
und können als
Flächen-Quadrate
dargestellt werden.
0
-2²
3²
y
-2
0
-1
1
0
2
1
3
Im ‚Einheiten-Raum‘
Pro UE wird eine Achse
verwendet. Bei n UEen ist
daher ein n-dimensionaler
Raum nötig.
Für jeden Wert, der genau
dem Mittel entspricht,
kann die Dimension um 1
reduziert werden.
Der Nullpunkt stellt den
Mittelwert dar. Auf jeder
Achse werden als Werte die
Differenzen zum Mittelwert
eingetragen.
Das Ergebnis ist ein
Datenpunkt für die gesamte
Stichprobe.
2
14/3 =
Var(y)
-1²
yy
1
2
4
3
5
Std(y) = 2.1
3
_
yi  y
yi
0
1
5
2
(yi  y )2
-2
-1
3
0
4
1
9
0
14
Var(y) = 14 / 3 = 4.66.
n
sq y
=
Var(y) :=
sq y : ( y i  y ) 2
n 1
i =1
_
3 y1
y
Der Einfachheit wegen werden die 3
Koordinaten mit a, b und c bezeichnet.
a
3 y2
d
_
y
b
-3
3
-3
_
y3
y
e
c
Berechnung der Distanz: wiederholte
Anwendung des Pythagoras-Satzes:
-2
-1
-3
Der quadrierte Abstand vom Nullpunkt zum
Datenpunkt ist genau die Summe der quadrierten
Abweichungen vom Mittelwert = Var(y) * (n-1)
Zuerst noch eine Hilfsebene einfügen.
Mit dem braunen Dreieck kann d auf Grund
von a und c berechnet werden: d2 = a2 + c2.
Mit dem lila Dreieck kann e auf Grund von d und
b berechnet werden: e2 = d2 + b2.
Nun ist e schon die gesuchte Distanz, quadriert:
e2 = d2 + b2 = a2 + c2 + b2.
Schiefe der Verteilung
Schiefemaß: schiefe(X)
Bei linksschiefen Verteilungen
ist das arithmetische Mittel
links(kleiner) vom Median.
Daher ist dann die Differenz
arithmetisches Mittel minus
Median negativ.
Bei symmetrischer Verteilung
ist diese Differenz 0 und bei
rechtsschiefer Verteilung positiv.
Beispiele für unterschiedliche Verteilungen:
symmetrisch
rechtsschief
linksschief
Schiefemaß
x  ~x 0.5
schiefe ( x ) :=
std(x)
xi
ni
xi
ni
xi
ni
0
1
2
1
3
6
0
1
2
2
6
2
0
1
2
6
3
1
1  schiefe(x)  1
Anteil
0. 6
linksschief
symmetrisch
rechtsschief
0. 5
Die Division durch die
Standardabweichung normiert
den Schiefekoeffizient (siehe
MOOD et al. 1974, S. 76)
0. 4
0. 3
0. 2
0. 1
0
arithm. Mittel
- Median
0
1
2
0
1
2
0
*
*
*
schiefe(x) = -0.71
*
schiefe(x) = 0
1
2
*
*
schiefe(x) = 0.71
Box-Plot (bzw. Box-and-Whisker Plot)
Median als Querstrich eintragen.
Hinges ebenfalls eintragen.
Ad-Hoc-Beispiel mit n=11. Alters-Werte sortiert: 7, 18, 23, 24, 24.5, 25, 27,
28, 29, 32, 38. Median = 25. hu= 23.5; ho=28.5; h-Spread= ho- hu=5.
Bereiche: Innere Zäune = 16 bis 36. Äußere Zäune= 8.5 bis 43.5
Hinges mit einer Box (daher Box-Plot) verbinden
Nun kann das Feld durch Zäune (engl. Fences)
abgesteckt werden.
Der obere innere Zaun liegt 1.5* h-Spread über dem
oberen Hinge. Der untere innere Zaun liegt 1.5* h-Spread
unter dem unteren Hinge.
Der obere äußere Zaun liegt 3* h-Spread über dem
oberen Hinge. Der untere äußere Zaun liegt 3* h-Spread
unter dem unteren Hinge.
Alter
40
Jeder Wert zwischen dem innere Zaun und äußerem
Zaun wird durch einen Stern markiert.
h-Spread *1.5
Oberer innerer Zaun
h-Spread *1.5
Whisker
Oberer Hinge ho
30
h-Spread
25
Median
Unterer Hinge hu
20
Festlegung der Whiskers (=Schnurrbart).
Das sind die Linien (nach oben bzw. unten) bis zum
extremsten Wert, der noch innerhalb des inneren Zauns
liegt.
Box-Plot
35
Extremwerte-Markierung (Outlier, Ausreißer)
Jeder Wert außerhalb der äußeren Zäune wird durch einen
fetten Punkt markiert.
Oberer äußerer Zaun
15
Whisker
h-Spread *1.5
Unterer innerer Zaun
h-Spread *1.5
10
Unterer äußerer Zaun
Die Zäune gehören nicht zum Boxplot.
5
Streuungsmaße für qualitative Merkmale
Alle bisher behandelten Streuungsmaße bauen auf der Breite der
Verteilung auf. Das setzt für das Merkmal Intervallskalenniveau
voraus.
Für ein qualitatives Merkmal kann untersucht werden, inwiefern
die Anteilsmasse auf eine einzige Ausprägung bzw. einige wenige
Ausprägungen konzentriert ist (geringe Streuung), oder auf
mehrere Ausprägungen eher gleichmäßig verteilt ist (große
Streuung).
Modaldispersion: md
Der Anteil der Werte, die nicht in
der Modal-Ausprägung liegen.
Qualitative Varianz: qv
Hier werden alle Anteile
(quadratisch) berücksichtigt.
Modaldispersion
md ( x ) := 1  max( p1 ,..., p I )
0  md( x )  1 - 1/I
(bzw. mittlere Entropie)
Potentiell minimale mittlere Länge
von Informationen in Bits (bzw.
Nits), wenn alle Teilinformationen
(Ausprägungen des Merkmals)
optimal codiert werden.
0.60
0.60
0.40
0.40
0.20
0
11
16
ledig
4
16
Familienstand
Anteil
0.20
1
16
6
16
0
verlobt getrennt
5
16
ledig
5
16
verlobt getrennt
Anteilsmasse konzentriert sich
Anteilsmasse ist eher gleichmäßig
stark auf die Ausprägung‚ledig‘. auf die Ausprägungen aufgeteilt.
(geringe Streuung)
(große Streuung)
11
1
, p 2 = 164 , p3 = 16
.
Die Anteile sind p1 = 16
6
5
5
p1 = 16
, p 2 = 16
, p 3 = 16
.
11
.
Der größte Anteil ist max( p1 , p 2 , p3 ) = 16
6
max( p1 , p 2 , p 3 ) = 16
.
11
1  16
= 165 = 0.3125
Daher md =
6
10
md = 1  16 = 16 = 0.625
Qualitative Varianz
qv(x) := 1  (p12 + ... + p 2I )
= p1 (1  p1 ) + ... + p I (1  p I )
0  qv( x )  1 - 1/I
Entropie: h
Familienstand
Anteil
Entropie(in bits)
h(x) b := i=1 pi ld(pi )
= ln(12) h(x)
I
Entropie(in nits)
h(x) := 
I
p
i =1 i
ln(pi )
0  hx( x )  ln (I)
2
2
2
=
1 138
256
2
2
qv =1  ( 166 + 165 + 165 )
2
11
qv = 1  ( 16
+ 164 + 161 )
= 0.461
=
86
1 256
= 0.664
Zur Entwicklung optimaler Codes im Sinne der
Informationstheorie, später!
11
11
4
4
1
1
h(x) =  16 ln(16 )  16 ln(16 )  16 ln(16 )
 0.777 nits
h(x)b =h(x) / ln(2)= 1.4427 h(x)  1.12
h(x) =  16 ln(16 )  16 ln(16 )
6
6
10
5
 1.095 nits
h(x)b = 1.4427 h(x)  1.58
Überlegungen zur Entwicklung optimaler Binär-Codes
Die Entwicklung optimaler
Binärcodes entspricht dem
Finden einer optimalen
Fragestrategie bei Unsicherheit,
wobei jede Antwort nur binär
(etwa: nein/ja; bzw. 0/1) sein
darf.
Beispiel: Anne und Bert spielen ‚Felderraten‘ auf dem PC. Der PC wählt zufällig (jedes Feld
mit gleicher Chance) ein bestimmtes Feld auf einem Schachbrett.
Anne soll erraten, welches Feld ausgewählt ist. Der PC antwortet auf Annes Fragen jeweils mit
nein bzw. ja oder 0 bzw. 1.
Bert macht das auch. Beide wiederholen das Spiel öfters. Gewinner ist, wer pro Spiel am
wenigsten Fragen braucht.
Welches ist hier die optimale Fragestrategie?
1 2 3 4 5 6 7 8
z.B. für Suche von C8
A
1. Feld oberhalb der Mitte? 1.
B
C
2. Feld links der Mitte? 0.
*
D
3. Liegt es in Zeile A bzw. B? 0.
E
4. In Spalte 5 bzw. 6? 0.
F
5. In der Zeile C? 1.
G
6. Ist es in Spalte 7? 0.
H
Antwortfolge: 100010. Daher muss es Feld C8 sein.
Bei I Ausprägungen sind ld(I) Fragen
bei optimaler Fragestrategie
erforderlich, wenn die Chancen aller
Ausprägungen gleich sind.
Wie viele Fragen dieser Art sind nötig? 6. Mit 6 Fragen kann jedes der 64 Felder eindeutig
identifiziert werden.
Die 64 Felder entsprechen den Ausprägungen. Jede Frage kann 2 mögliche Antworten
haben. Daher insgesamt 26 = 64 mögliche Antwortsequenzen.
Der Logarithmus von 64 zur Basis 2 löst die Aufgabe: 2 hoch x = 64. D.h. x = ld(64) = 6.
Umgeformt: 6 = - ld(1/64).
Es gilt auch: ld(I) = -ld(1/I)
Bei ungleichen Anteilen sind andere
Fragestrategien besser.
Die optimale Strategie wird auf Grund
der Anteile entwickelt. Nach
Ausprägungen mit großem Anteil wird
zuerst gefragt.
z.B. Falls der PC fast immer das Feld C8 wählt, ist es wohl optimaler, zuerst zu fragen: Ist es
Feld C8?
Überlegungen zur Entwicklung optimaler Binär-Codes, Forts.
Die optimale Strategie wird auf Grund
der Anteile entwickelt.
Zuerst nach Ausprägungen mit dem
größten Anteil fragen;
danach die seltenen Fälle abklappern!
4-Buchstaben-Beispiel: Buchstaben A, B, C, D erraten. Anne weiß aus Erfahrung, dass der
PC A in ½, B in ¼, C in 1/8 und D in 1/8 der Fälle auswählt. Welche optimale
Fragestrategie soll sie wählen?
Vorschlag: Zuerst nach A fragen., weil der Anteil mit ½ am größten ist (Die Chance, nach der
ersten Frage fertig zu sein ist groß). Falls nein nach B fragen (wegen ¼ Chance). Falls nein,
nach C fragen.
Fragestrategie in Form eines Flussdiagramms
Für das Erraten von: A
benötigte Fragenanzahl 1
Anteil
½
Optimal?
Erwartete Fragelänge(in bits)
I
piFragenanzahl i
i=1
B
2
¼
C
D
3
3
1/8 1/8
Durchschnittlich benötigte Anzahl
‚optimaler‘
Entropie(in bits)
Fragen = h ( x ) := 
b
iI=1 pi ld(pi )
Für das Erraten von:
benötigte Fragenanzahl
Anteil
1/Anteil
ld(1/Anteil)
A
1
½
2
1
B
2
¼
4
2
Das gewichtete arithmetische Mittel:
kann dann so ausgedrückt werden:
Übersetzen des Fragespiels in die
Übermittlung von Nachrichten.
Eine Antwortsequenz entspricht einem
Binärcode, die Länge des Binärcodes
(gemessen in bit) der Fragenanzahl.
Übertragen vieler gleicher Ausprägungen
in einer Nachricht als Packet.
1
A
0
B?
1
B
0
C?
0
1
D
C
Das Spiel werde nun sehr oft wiederholt. Mit Hilfe der Anteile als Gewichte kann nun die
durchschnittlich benötigte Fragenlänge berechnet werden : ½ mal 1, ¼ mal 2, 1/8 mal 3 1/8 mal 3.
½ * 1 + ¼ * 2 + 1/8* 3 + 1/8*3 = 14 / 8
Als gewichtetes arithmetische Mittel:
Bei passenden Anteilen gilt:
Fragenanzahl = ld(1/pi) = -ld(pi )
A?
C
3
1/8
8
3
D
3
1/8
8
3
½ * 1 + ¼ * 2 + 1/8 * 3 + 1/8 * 3.
- (½ * ld(½ ) + ¼ *ld(¼) + 1/8 *ld(1/8) + 1/8 *ld(1/8))
Das Übertragen von Nachrichten ist kein kompetitives, sondern ein kooperatives ‚Spiel‘.
Der Binärcode für alle Ausprägungen eines Merkmals (ein Alphabet, die Bezeichnung der 64 Schachfelder, die
4 Ausprägungen A B C D) optimal aufgebaut werden, damit zur Übertragung von Nachrichten (mit dem
betrachteten Alphabet) möglichst wenig binäre Zeichen notwendig sind.
Die Antwortsequenz für eine einzelne Ausprägung entspricht dem Binärcode der Ausprägung (z.B. 100010 für
C8 innerhalb des Schachalphabets, im 4-Buchstaben-Beispiel 1 für A , 01 für B, 001 für C und 000 für D).
Wenn in Nachrichten oft mehrere gleiche Ausprägungen hintereinander übertragen werden müssen, kann ein
Wiederholungsmodus (eine zahlenmäßige Information derart, dass z.B.100 gleiche Zeichen folgen usw.) eingebaut
werden. So kann die (potentiell minimale) durchschnittliche Informationslänge auch kleiner als 1 Bit werden.
Rest
Anteilsverteilung
Sortierte Liste
Index
(i)
Wert
x(i)
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
21
21
21
21
21
21
22
22
22
22
23
23
24
24
24
30
ui
1
2
3
4
5
0
100
500
1000
2000
.0010
.0009
.0008
.0007
.0006
.0005
.0004
.0003
.0002
.0001
0
Anteil
Klassen
Mitte
oi
pi
xi
100
500
1000
2000
5000
0.10
0.10
0.20
0.30
0.30
100
400
500
1000
3000
Klassen
Grenzen
Klassen
Index
i
f(x)
0
1.0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.0
1000
2000
3000
4000
5000
3000
4000
5000
F(x)
0
1000
2000
x
Das Verhältnis der Flächen ist gleich
dem Verhältnis der Längen:
p / q = b m/ s
.0010 m m
.0009
Daher: s = qmb m/ pm .
.0008
.0007
.0006
.0005
.0004
.0003
.0002
.0001
0
.0010
.0009
.0008
.0007
.0006
.0005
.0004
.0003
.0002
.0001
0
f(x)
F(u m)
0
1000
2000
um
s
~
xq
3000
4000
5000
f(x)
0
1000
2000
3000
4000
5000
.0010
.0009
.0008
.0007
.0006
.0005
.0004
.0003
.0002
.0001
0
f(x)
0
1000
625
~
200 x 0.25
e
2000
3000
2500
~
x 0.75
4000
5000
3750
e
~
Gesucht: x¼ , daher ist q = 0.25. Index m = 3. Erst hier ist
F(o3) > 0.25. u3= 500. F(u3) = F(500) = 0.20. Daher ist das
~
1. Quartil x¼ = 500 + (0.25-0.20)500/ 0.20 = 625.
Begründung der Formel für das Quantil
1.0
0.9
q = 0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.0
Jeder Klasse entspricht eine Gerade.
Für q muss festgestellt werden, welche Gerade benötigt wird.
Die Geradengleichung allgemein ist: y = a + bx. Die Gerade geht durch die
Punkte (u m, F(u m) ) und (o m, F(o m) ) .
F( o ) F( u )
a und b kann durch Einsetzen der Punkte
b = om u m , a = F(u m )  bu m
m
m
in die Gleichung berechnet werden.
~
q = a + bx q  ~
x q = (q  a ) / b
Nun wird der Punkt (~
xq , q) in die
1
~
Gleichung eingesetzt.
x q = (q  F(u m ) + bu m ) b
F(x)
0
1000
2000 ~ 3000
xq
4000
5000
x
Weiteres Umformen und Einsetzen
von a und b liefert die Formel:
o u
~
x q = u m + (q  F(u m )) F( u mm) Fm( u m )
n
sq y
Var(y) :=
sq y :=( y i  y ) 2
n 1
i =1
3
Varianz
3
-3
3
-1
Quadratsummen
-3
-2
-1
für Verteilung:
I
sq x := n  p i ( x i  x ) 2
i =1
-3
1 2 3 4 5 6 7 8
A
B
C
D
E
F
G
H
Der Einfachheit wegen werden die 3
Koordinaten mit a, b und c bezeichnet.
a
b
Berechnung der Distanz: wiederholte
Anwendung des Pythagoras Satzes.
c
Berechnung der Distanz: wiederholte
Anwendung des Pythagoras Satzes.
Zuerst noch Hilfsebene einfügen
Andere Mittelwerte, Geometrisches Mittel
Das geometrische Mittel
ist die n-te Wurzel aus
dem Produkt aller Werte.
An die Stelle des Addierens tritt das
Multiplizieren. Statt durch n zu dividieren, wird die n-te Wurzel gezogen.
Das arithmetische Mittel
der logarithmierten
Werte ist der
Logarithmus des
geometrischen Mittels.
Bei Wachstumsfaktoren
liefert das geometrische
Mittel die adäquate
Berechnung des Endwerts
aus dem Anfangswert.
Für Urliste:
xG = n x1 x2 ... xn
n
= n  xi
i =1
Beispiel (Eine Firma habe seit 4 Jahren des Bestehens folgende
Gewinne: 200, 400, 300, 300).
Der Wachstumsfaktor des Gewinns ist hier das Verhältnis des
jeweiligen Gewinns zum Vorjahresgewinn.
Das ergibt 3 Wachstumsfaktoren: x1=400/200=2, x2 =0.75, x3 =1.
x G = 3 20.751 = 1.14 (etwas anders formuliert: das ist
ein durchschnittliches Wachstum von 14 %).
Auf beiden Seiten
Logarithmieren liefert:
log(x G ) =
n
1
n
 log(x i )
i =1
Die Formel gilt für jede Art von Logarithmus, hier wird der zur
Basis e verwendet (natürlicher Logarithmus):
ln(x G ) = 13 (ln(2) + ln(0.75) + ln(1))  13 0.405465
Aus dem Logarithmus einer Zahl kann mit Hilfe des Potenzierens
der Basis die Zahl selbst berechnet werden:
x G = exp(ln(x G )) = exp( 13 0.405465) = 1.14
Wendet man den durchschnittlichen Wachstumsfaktor pro Jahr seit Beginn an: 200*1.14*1.14*1.14
=300. Der tatsächliche Gewinn am Ende kann damit vom Anfang her mit Hilfe des durchschnittlichen
Wachstums berechnet werden.
Das arithm. Mittel der Wachstumsfaktoren = 1.25 (=25% Wachstum; etwas größer). Wendet man dies
als durchschnittliches Wachstum über die Jahre an wie vorher, erhält man: 200*1.25*1.25*1.25
=390.625 (Wohl etwas zu optimistisch).
Voraussetzungen und Eigenschaften des geometrischen Mittels
Das Merkmal muss mindestens Verhältnisskalenniveau haben. Die Werte sollten positiv sein.
Generell ist das geometrische Mittel ist kleiner (bzw. gleich) als das arithmetische.
Wenn über Wachstumsfaktoren gemittelt wird, sollte statt des arithmetischen auf jeden Fall das geometrische Mittel
verwendet werden.
Verteilungscharakterisierung durch Funktionen der Anteile
Verhältnisangaben
(engl. Odds), beim Wetten als Angabe zur Charakterisierung der Chancen
Als Darstellung interessiert
das Verhältnis der Anteile
(Häufigkeiten) zueinander
bzw. zu einer ‚Referenz‘Ausprägung.
Logit.
Odds
oddsj(pi ) := pi : pj = pi/pj
mit j als Index für die
Referenzausprägung
Beispiel: Bei Sex unter den ersten 16 ist der ‚männlich‘-Anteil
=14/16, der ‚weiblich‘-Anteil=2/16. Als Verhältnis 14 : 2 bzw.
7:1 mit ‚weiblich‘ als Referenzkategorie. bzw. (1/7) : 1 mit
‚männlich‘ als Referenzkategorie bzw. 0.1428 : 1
Beispiel: Nach MENDEL sollten 4 Erbsensorten bei einem
Kreuzungsexperiment im Verhältnis 9 : 3 : 3 : 1 stehen (Angaben
als Odds). Die Häufigkeiten beim MENDEL’schen Experiment
waren: 315, 108, 101, 32. Mit der 4. Ausprägung als Referenzkategorie lauten die realisierten Odds: 9.8 : 3.375 : 3.156 : 1
Der Logit ist der natürliche Logarithmus der Odds.
Die Verhältnisse werden
logarithmiert; so werden die
‚multiplikativen‘
Verhältnisangaben ‚additiv‘.
Logits
Logitj(pi ) := ln( pi /pj )
= ln(pi )-ln(pj).
mit j als Index für die
Referenzausprägung
Beispiel: Logit für den ‚männlich‘-Anteil
logit(14/16) =ln(7) = 1.96.
Der Logit für den ‚weiblich‘- Anteil
logit(14/16)=ln(1/7) = -1.96.
Durch das Logarithmieren erhält man bei zwei Ausprägungen den gleichen Wert (einmal positiv, einmal negativ). Die
Wahl der Referenzausprägung ist dadurch nicht mehr so wichtig.
Bei den Odds versucht man, die Referenzausprägung so zu wählen, dass möglichst als Verhältnis Werte größer als 1
resultieren (bei Odds für Teilgruppen schwer realisierbar).