Lösungen:
Werbung

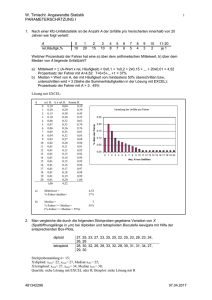
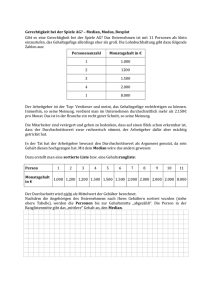
Lösungen 1. a/ X =22.89 T€ ̂ 6.82 T€ b/ Die Parameter der Normalverteilung sind somit: m= X =22.89 T€ 6.82 T€ P(X>31T€)=1-P P(X<31T€)=1- 0.88279= 0.117 (die Schätzung durch die originalen Daten ist 0). c/ Var(Rel.Hfgk)=p(1-p)/n, aber p ist jetzt unbekannt. p(1-p)≤1/4, also wir bekommen aus dem Tschebischev’schen Ungleichung, dass P(|Rel.Hfgk-p|>0.1) ≤100/(4n) ≤ 0.05 falls n≥500 Durch die Normalverteilung: Falls wir davon ausgehen, dass die Rel.Hfgk einer Normalverteilung mit Varianz 1/(4n) folgt, dann gilt P(|Rel.Hfgk-p|>0.1)=2*(1Φ(sqrt(n)/5)) ≤ 0.05 falls Φ(sqrt(n)/5)) ≥0,975, also n≥96,04 (es bedeutet praktisch, dass wir wenigstens 97 Beobachtungen) brauchen. 2. 10 Firmen wurden zu ihrem Jahresumsatz im Jahr 2008 befragt (die Werte sind in MFt). Wir interessieren uns für den Median und in das 85% Quantil des Umsatzes. 60 72 84 88 89 93 103 103 120 126 a/ Geben Sie Schätzungen für den Median und das 85%-Quantil des Jahresumsatzes. b/ Wir haben nur diese 10 Beobachtungen, aber wir möchten etwas sagen über die Streuung unsere Schätzungen, ohne die Verteilung der Beobachtungen zu bestimmen. Deshalb führen wir die sogenannte bootstrap Methode aus. Geben wir Schätzungen für die Standardabweichung des Medians und des 85% Quantils mit der Hilfe der folgenden bootstrap Stichproben. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 60 88 60 60 84 60 60 72 84 60 88 88 72 60 84 60 84 84 84 84 89 93 72 84 84 72 84 84 84 84 93 103 103 103 120 120 120 93 93 103 103 120 126 126 84 93 103 103 120 126 126 84 84 84 93 103 120 126 88 88 88 103 126 126 126 88 89 103 103 120 120 126 88 89 93 103 103 103 120 93 103 103 103 120 126 126 88 88 88 103 103 120 126 84 89 89 89 93 103 126 a) Der Median der original Daten beträgt 91 MFt. Das 85% Quantil der original Daten beträgt 120 MFt Im weiteren müssen Sie nun für jede Zeilen 1 bis 10 der Stichproben jeweils den Median und das 85% Ouantil bestimmen. So bekommen Sie untenstehende Werte Median 103 98 98 84 88 96 91 103 88 89 Beispiel: In der ersten Zeile ist der Median 103 (0,5x (103 +103)) 85% Quantile 120 126 126 120 126 120 103 126 120 103 Beispiel: in der ersten Zeile ist das 85% Quantil 120 (Neunter Wert) b) Nun können Sie die Standardabweichung für den Median und das 85% Quantil bestimmen. Standardabweichung für Median: 7.3 MFt Wurzel aus ((103-91)²+(98-91)²+……..+(103-91)²)/9 Standardabweichung für 85% Quantile: 9 MFt Wurzel aus ((120-120)²+(126-120)²+……..+(103-120)²)/9 3. X = 4,95 2 X =9,9 es ist Erwartungstreu a.) b.) max (X) = 8. Dieser Wert ist ein Unterschätzung. Er ist nicht erwartungstreu (aber es kann verbessert werden mit ein Faktor von (n+1)/n und man kann zeigen z.B. durch Simulation, das dieser Wert effektiver ist als die anderen) In unser Fall ergibt sich 11*8/10=8,8 Min