Eine Frau hat Blutgruppe 0 (Genotyp 00), ihre Tochter Blutgruppe A
Werbung
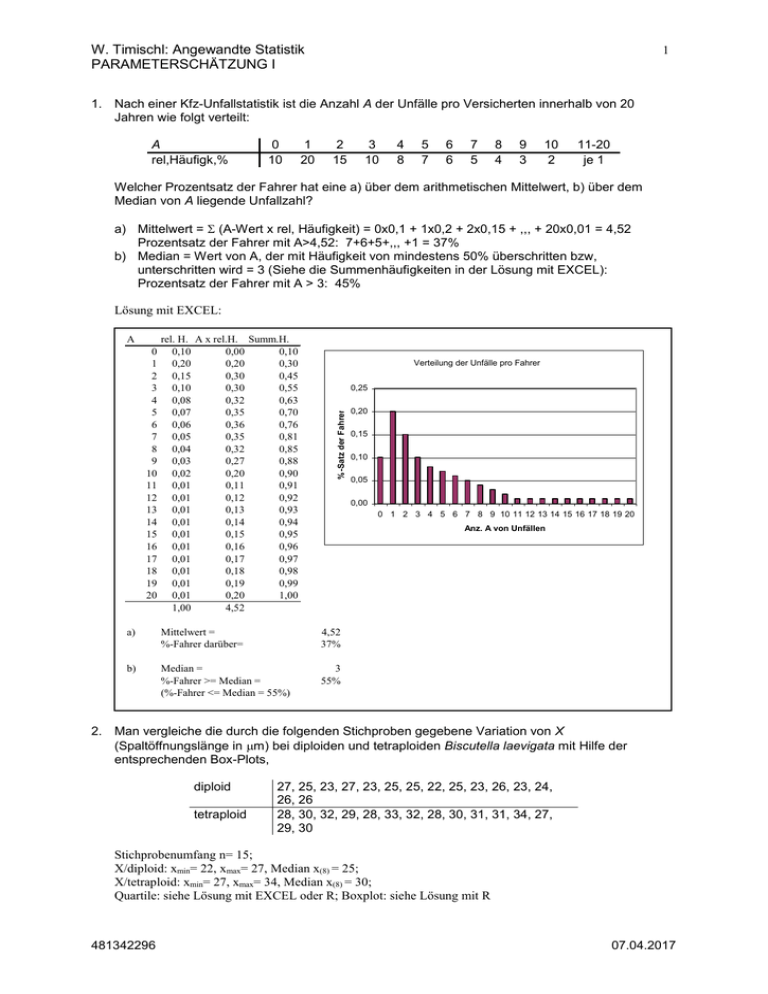
W. Timischl: Angewandte Statistik PARAMETERSCHÄTZUNG I 1 1. Nach einer Kfz-Unfallstatistik ist die Anzahl A der Unfälle pro Versicherten innerhalb von 20 Jahren wie folgt verteilt: A rel,Häufigk,% 0 10 1 20 2 15 3 10 4 8 5 7 6 6 7 5 8 4 9 3 10 2 11-20 je 1 Welcher Prozentsatz der Fahrer hat eine a) über dem arithmetischen Mittelwert, b) über dem Median von A liegende Unfallzahl? a) Mittelwert = (A-Wert x rel, Häufigkeit) = 0x0,1 + 1x0,2 + 2x0,15 + ,,, + 20x0,01 = 4,52 Prozentsatz der Fahrer mit A>4,52: 7+6+5+,,, +1 = 37% b) Median = Wert von A, der mit Häufigkeit von mindestens 50% überschritten bzw, unterschritten wird = 3 (Siehe die Summenhäufigkeiten in der Lösung mit EXCEL): Prozentsatz der Fahrer mit A > 3: 45% Lösung mit EXCEL: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 rel. H. A x rel.H. Summ.H. 0,10 0,00 0,10 0,20 0,20 0,30 0,15 0,30 0,45 0,10 0,30 0,55 0,08 0,32 0,63 0,07 0,35 0,70 0,06 0,36 0,76 0,05 0,35 0,81 0,04 0,32 0,85 0,03 0,27 0,88 0,02 0,20 0,90 0,01 0,11 0,91 0,01 0,12 0,92 0,01 0,13 0,93 0,01 0,14 0,94 0,01 0,15 0,95 0,01 0,16 0,96 0,01 0,17 0,97 0,01 0,18 0,98 0,01 0,19 0,99 0,01 0,20 1,00 1,00 4,52 Verteilung der Unfälle pro Fahrer 0,25 %-Satz der Fahrer A 0,20 0,15 0,10 0,05 0,00 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Anz. A von Unfällen a) Mittelwert = %-Fahrer darüber= 4,52 37% b) Median = %-Fahrer >= Median = (%-Fahrer <= Median = 55%) 3 55% 2. Man vergleiche die durch die folgenden Stichproben gegebene Variation von X (Spaltöffnungslänge in m) bei diploiden und tetraploiden Biscutella laevigata mit Hilfe der entsprechenden Box-Plots, diploid tetraploid 27, 25, 23, 27, 23, 25, 25, 22, 25, 23, 26, 23, 24, 26, 26 28, 30, 32, 29, 28, 33, 32, 28, 30, 31, 31, 34, 27, 29, 30 Stichprobenumfang n= 15; X/diploid: xmin= 22, xmax= 27, Median x(8) = 25; X/tetraploid: xmin= 27, xmax= 34, Median x(8) = 30; Quartile: siehe Lösung mit EXCEL oder R; Boxplot: siehe Lösung mit R 481342296 07.04.2017 W. Timischl: Angewandte Statistik PARAMETERSCHÄTZUNG I Lösung in EXCEL: 2 nach aufsteigender größe geordnete Stichproben: X/diploid X/tetraploid 22 27 22 28 23 28 23 28 23 29 24 29 25 30 25 30 25 30 25 31 26 31 26 32 26 32 27 33 27 34 22 27 27 34 xmin=MIN(Bereich)= xmax=MAX(Bereich)= Median=QUANTIL(Bereich;0,50)= 25%-Quantil=QUANTIL(Bereich;0,25)= 75%-Quantil=QUANTIL(Bereich;0,75)= 25 23 26 30 28,5 31,5 22 24 26 28 30 32 34 Lösung mit R: xdiploid <- c( + 27, 25, 23, 27, 23, 25, 25, 22, 25, 23, 26, 23, 24, 26, 26) > xtetraploid <- c( + 28, 30, 32, 29, 28, 33, 32, 28, 30, 31, 31, 34, 27, 29, 30) > summary(xdiploid) Min, 1st Qu, Median Mean 3rd Qu, Max, 22,00 23,00 25,00 24,67 26,00 27,00 > summary(xtetraploid) Min, 1st Qu, Median Mean 3rd Qu, Max, 27,00 28,50 30,00 30,13 31,50 34,00 > boxplot(xdiploid, xtetraploid) 1 481342296 2 07.04.2017 W. Timischl: Angewandte Statistik PARAMETERSCHÄTZUNG I 3 3. Die Messung der Ozonkonzentration während der Sommermonate ergab für eine Großstadt die in der folgenden Tabelle enthaltenen Werte (Angaben in 10-2 ppm), Man stelle die Verteilung der Ozonkonzentration dar (tabellarisch, grafisch) und berechne den Mittelwert, die Standardabweichung, den Median und die Quartile, 3,6 1,5 6,6 6,0 4,2 6,7 2,5 5,4 4,5 5,4 2,5 3,0 5,6 4,7 6,5 6,7 1,7 5,3 4,6 7,4 5,4 4,1 5,1 5,6 5,4 6,1 7,6 6,2 6,0 5,5 5,8 8,2 3,1 5,8 2,6 9,5 3,4 8,8 7,3 1,3 6,9 3,2 4,7 3,8 5,9 6,6 4,4 5,7 4,5 7,7 Lösung mit EXCEL: 3,6 1,5 6,6 6,0 4,2 6,7 2,5 5,4 4,5 5,4 MIN=MIN(Bereich)= MAX=MAX(Bereich) Spannweite=MAX-MIN= n=ANZAHL(Bereich) Anz.Klassen=RUNDEN(WURZEL(50);0)= Intervallbreite = Spannweite/Anz.Klassen (gerundet)= Mittelwert=MITTELWERT(Bereich)= Standardabweichung=STABW(Bereich)= Median = QUANTIL(Bereich;0,5)= 25%-Quantil=QUANTIL(Bereich;0,25)= 75%-Quantil=QUANTIL(Bereich;0,75)= Häufigkeitsverteilung: 2,5 3,0 5,6 4,7 6,5 6,7 1,7 5,3 4,6 7,4 5,4 4,1 5,1 5,6 5,4 6,1 7,6 6,2 6,0 5,5 5,8 8,2 3,1 5,8 2,6 9,5 3,4 8,8 7,3 1,3 6,9 3,2 4,7 3,8 5,9 6,6 4,4 5,7 4,5 7,7 1,3 9,5 8,2 50 7 1,5 5,2 1,852 5,4 4,125 6,425 UG OG Mitte a.H. r.H. 1,0 2,5 1,75 5 0,10 2,5 4,0 3,25 7 0,14 4,0 5,5 4,75 15 0,30 5,5 7,0 6,25 16 0,32 7,0 8,5 7,75 5 0,10 8,5 9,0 8,75 1 0,02 9,0 10,5 9,75 1 0,02 50 1 18 15 16 abs. Häufigkeit 15 12 9 6 7 5 5 3 1 1 8,75 9,75 0 1,75 3,25 4,75 6,25 7,75 Klassenmitte 481342296 07.04.2017 W. Timischl: Angewandte Statistik PARAMETERSCHÄTZUNG I 4 Lösung mit R: > ozon <- c( + 3.6, 6.7, 2.5, 6.7, 5.4, 6.1, 5.8, 9.5, 6.9, 6.6, + 1.5, 2.5, 3.0, 1.7, 4.1, 7.6, 8.2, 3.4, 3.2, 4.4, + 6.0, 4.5, 4.7, 4.6, 5.6, 6.0, 5.8, 7.3, 3.8, 4.5, + 6.6, 5.4, 5.6, 5.3, 5.1, 6.2, 3.1, 8.8, 4.7, 5.7, + 4.2, 5.4, 6.5, 7.4, 5.4, 5.5, 2.6, 1.3, 5.9, 7.7) > summary(ozon) Min. 1st Qu. Median Mean 3rd Qu. Max. 1.300 4.125 5.400 5.212 6.425 9.500 > sd(ozon) [1] 1.851821 > hist(ozon, freq=TRUE, xlab="Ozonkonz.in 1/100 ppm", ylab="abs. Klassenhäufigkeit", + main="Verteilung der Ozonwerte/abs. Klassenhäufigkeiten, n=50", ylim=c(0,20)) 10 0 5 abs. Klassenhäufigkeit 15 20 Verteilung der Ozonwerte/abs. Klassenhäufigkeiten, n=50 2 4 6 8 10 Ozonkonz.in 1/100 ppm 481342296 07.04.2017