2 Maßzahlen_Präsentation

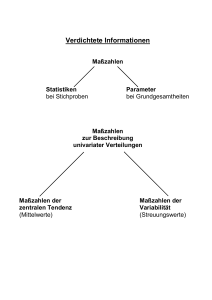
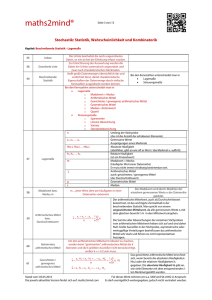
Einfache Maßzahlen
Tamara Katschnig
Einführung



Deskriptive (Beschreibende) Statistik
Stellt Untersuchungsergebnisse dar, fasst
sinnvoll zusammen
Charakterisiert Stichproben durch
geeignete Kenngrößen, die einfachsten
statistischen Kenngrößen bzw. Formen
der Quantifizierung kennen Sie alle:
Häufigkeiten und Prozent
2
Einführung



Dadurch wird ermittelt wie oft
verschiedene Ausprägungen eines
Merkmals in der Grundgesamtheit
(Stichprobe) auftreten.
z. B.: wie viele Neugeborene sind
weiblich/männlich
eine Voraussetzung für das
Quantifizieren/Zählen = qualitative
Gleichartigkeit der Objekte!
3
Drei Darstellungsarten



Tabelle (Häufigkeitsverteilungen)
Grafik (anschaulich): Säulen-,
Balkendiagramm (Achtung auf y-Achse),
Kreisdiagramm, Liniendiagramm,
Punktdiagramm, Streudiagramm
Maßzahlen (Mittelwert etc. schneller
Vergleich möglich)
4
Tabelle
Vege- Normal Zeilensumme
tarier esser
weiblich
35
90
125
männlich
15
110
125
Spaltensumme 50
200
250=N
5
Grafiken
25,0%
20,0%
15,0%
10,0%
5,0%
0,0%
Zi gar et t en
Große Anst rengung
K af f ee
St ress
A l kohol
M edi kament e
Emot ionale Überf orderung
6
Maßzahlen: Mittelwert, Median, Modalwert





Geben einen Eindruck der Höhe der
beobachteten Messwerte
Mittelwert = arithmetisches Mittel
Ist die Summe aller Messwerte
dividiert durch die Anzahl
z.B. Notendurchschnitt einer
Schülerin
x=1/8.Σ1+2+2+3+1+4+2+1=2
7
Maßzahlen: Mittelwert, Median, Modalwert


Modalwert = häufigster Wert,
relative Mehrheit, besonders
typischer Ausgang, aber nicht die
Mitte!!
z.B.
Schüler A: 2 2 3 5 4 2 x=3
Schüler B: 3 3 3 3 3 3 x=3
Modalwert bei A=2, bei B=3
8
Maßzahlen: Mittelwert, Median, Modalwert





Median = mittlerer Wert nach Ordnen der
Messwerte, genauso viele darüber wie
darunter = robustes Maß
z.B. Einkommen 1200 1200 1300 1400
1700 9000 12000
x=??, Modalwert=??, Median=??
wenn n = gerade, kein Median,
Durchschnitt mittlerer Werte
z. B. 1 3 4 7, Median= 3+4/2=3,5
9
Varianz=Streuung
Die Varianz ist ein Maß, das beschreibt,
wie stark eine Messgröße (genauer eine
Zufallsgröße) „streut“. Sie wird berechnet,
indem man die Abstände der Messwerte
vom Mittelwert quadriert, addiert und
durch die Anzahl der Messwerte teilt.
Die Varianz der Zufallsvariable X wird
üblicherweise als σ2 notiert.
10
Standardabweichung
Ihr Nachteil (Varianz) für die Praxis ist,
dass sie eine andere Einheit als die Daten
besitzt. Dieser Nachteil kann behoben
werden, indem man statt der Varianz die
Standardabweichung benutzt.
Die Standardabweichung ist die
Quadratwurzel der Varianz.
11
Übung 2
6)
8)
9)
10)
11)-15)
12