8. Statistik
Werbung
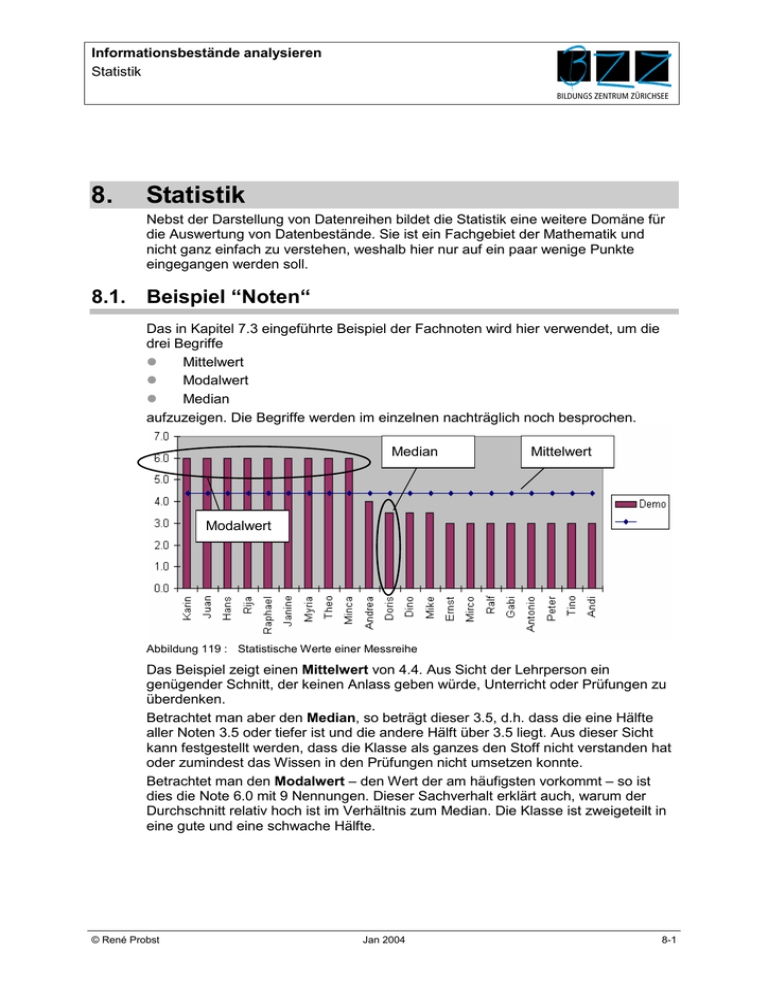
Informationsbestände analysieren Statistik 8. Statistik Nebst der Darstellung von Datenreihen bildet die Statistik eine weitere Domäne für die Auswertung von Datenbestände. Sie ist ein Fachgebiet der Mathematik und nicht ganz einfach zu verstehen, weshalb hier nur auf ein paar wenige Punkte eingegangen werden soll. 8.1. Beispiel “Noten“ Das in Kapitel 7.3 eingeführte Beispiel der Fachnoten wird hier verwendet, um die drei Begriffe Mittelwert Modalwert Median aufzuzeigen. Die Begriffe werden im einzelnen nachträglich noch besprochen. Median Mittelwert Modalwert Abbildung 119 : Statistische Werte einer Messreihe Das Beispiel zeigt einen Mittelwert von 4.4. Aus Sicht der Lehrperson ein genügender Schnitt, der keinen Anlass geben würde, Unterricht oder Prüfungen zu überdenken. Betrachtet man aber den Median, so beträgt dieser 3.5, d.h. dass die eine Hälfte aller Noten 3.5 oder tiefer ist und die andere Hälft über 3.5 liegt. Aus dieser Sicht kann festgestellt werden, dass die Klasse als ganzes den Stoff nicht verstanden hat oder zumindest das Wissen in den Prüfungen nicht umsetzen konnte. Betrachtet man den Modalwert – den Wert der am häufigsten vorkommt – so ist dies die Note 6.0 mit 9 Nennungen. Dieser Sachverhalt erklärt auch, warum der Durchschnitt relativ hoch ist im Verhältnis zum Median. Die Klasse ist zweigeteilt in eine gute und eine schwache Hälfte. © René Probst Jan 2004 8-1 Modul-100 Theorie 8.2. Mittelwerte Der Mittelwert ist einer der häufigsten statistischen Werte, die verwendet werden. Er sagt aus, welcher Wert – rein mathematisch – sich im Mittel aus allen Werten ergeben würde. Der Begriff Mittelwert ist dabei ungenau, da in der Mathematik verschiedene Mittelwerte existieren, eigentlich müsste man vom arithmetischen Mittel sprechen. Es werden alle Werte der Messreihe addiert und durch die Anzahl der Werte dividiert. (Bei Excel ist dies die Funktion MITTELWERT) Dieses Mass wird bei technischen Messvorgängen erhoben. Zusätzlich ist es aber auch wichtig zu wissen, wie präzise denn dieser Mittelwert ist. Man spricht in diesem Fall von der Standardabweichung. Sie ist ein Mass, das aussagt, wie zuverlässig der Mittelwert erreicht wird. Unter „Zuverlässig“ versteht man, dass 63% aller Messungen innerhalb eines Bereichs um den Mittelwert sind, der durch die Standardabweichung gegeben ist. (Bei Excel ist dies die Funktion STABW) Beispiel : Mittelwert und Standardabweichung einer Messreihe mit 50 Messpunkten Verteilung 9 Mittelwert = 13.3 8 7 Standardabweichung = 5.32 6 5 Reihe2 4 3 2 1 29 27 25 23 21 19 17 15 13 11 9 7 5 3 1 0 Abbildung 120 : Messreihe mit Mittelwert und Standardabweichung Häufig genügt aber zur Charakterisierung einer statistischen Masse die Darstellung der Häufigkeitsverteilung nicht. Man zieht oft zusätzliche Mittelwerte heran, die eine Vorstellung über die mittleren Werte einer Verteilung geben sollen. Diese Mittelwerte werden nach zwei verschiedenen Kriterien charakterisiert: 8-2 Modul 100 V1.2b.doc Abteilung Informatik/Technik Informationsbestände analysieren Statistik 1. Lagetypische Mittelwerte 2. Rechentypische Mittelwerte Die lagetypischen Mittelwerte werden von dem in der Mitte der Verteilung liegenden Wert bestimmt. Es sind dies der häufigste Wert (Modus) und der zentrale Wert (Median). Bei der Berechnung der rechentypischen Mittelwerte wird jeder einzelne Wert der Verteilung berücksichtigt. Rechentypische Mittelwerte sind: 1. Arithmetisches Mittel 2. Geometrisches Mittel 3. Harmonisches Mittel (wird in diesem Zusammenhang nicht erklärt) © René Probst Jan 2004 8-3 Modul-100 Theorie 8.3. Modus18 Der Modus XMo ist der, mit der grössten Häufigkeit auftretende Wert einer statistischen Variablen. Er wird auch "dichtester Wert" genannt (Wert mit der größten Dichte). Definition des Modus: XMo = xi mit fi = max xi ist dabei der i-te Messwert, während fi die Funktion ist, die das Maximum aller i Messwerte sucht. Der Modus kann stets dem Säulendiagramm oder dem Histogramm entnommen werden. (Bei Excel ist dies die Funktion MODALWERT) Verteilung Modalwert = 12 9 8 7 6 5 Reihe2 4 3 2 1 0 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 Abbildung 121 : Modalwert aus Säulendiagramm Das Beispiel zeigt, dass der häufigste Wert 12 in der Messreihe achtmal vorkommt 18 8-4 auch Modalwert genannt Modul 100 V1.2b.doc Abteilung Informatik/Technik Informationsbestände analysieren Statistik 8.4. Median Der Median oder Zentralwert ist jener Wert einer statistischen Variablen, welcher die der Größe nach geordneten Werte in genau zwei Hälften teilt. Es liegen rechts und links des Medians je 50% der Größe nach geordneten Werte. Für die Ermittlung des Medians (xMe) sind die Zähl- oder Messergebnisse immer zuerst in eine geordnete Reihe zu bringen. Wenn z.B. 7 Daten vorliegen, sind sie zur Medianbestimmung in folgende Reihenfolge zu bringen: xl <= x2 x2 <= x3 x3 <= x4 x4 <= x5 x5 <= x6 x6 <= x7 d.h. die Werte sind aufsteigend zu ordnen, wobei so x4 zum Median oder Zentralwert wird, da links und rechts von ihm 50% der Beobachtungen – in diesem Fall sind es 3 Messwerte - liegen. Der Median kann nie bei einem Extremwert einer Verteilung liegen und wird. auch nicht durch die Größe von Extremwerten in seiner Lage beeinflusst. Für die Bestimmung des Medians ist zu unterscheiden, ob die Zahl der vorliegenden Daten, die wir allgemein mit n bezeichnen, gerade oder ungerade ist. Medianbestimmung Fall 1: ungerade: Fall 2: gerade: xMe = x(n+1)/2 xMe = (x(n/2 + x(n+2)/2)/2 Bei ungerader Anzahl an Beobachtungen ist also der Median jener Wert der statistischen Variablen, für den der laufende Index i = (n+ 1) : 2 ist. 8.4.1. Optimale Entfernung Durch den Median kann man jenen Wert bestimmen, von dem aus die Summe der Entfernungen (absolut genommen) zu den anderen Werten der Häufigkeitsverteilung ein Minimum ergibt: P ¦ xi – xMe ¦ = Min. Will eine Zulieferfirma ein Zentrallager errichten, von dem aus verschiedene, entlang einer Straße liegende, Betriebe beliefert werden sollen, so gibt der Median jenen © René Probst Jan 2004 8-5 Modul-100 Theorie Standort an, von dem aus die Summe der Distanzen zu den Betrieben den kleinsten Wert annimmt. Liegen die Betriebe z.B. bei Kilometer 210,230,260,340 und 360, so ist die kleinste absolute Abstandssumme erreicht, wenn das Auslieferungslager bei km 260, also dem Median, errichtet wird. Im bisher gezeigten Beispiel liegen die Messwerte zwischen 1 und 26. In diesem Fall liegt der Median zwischen 13 und 14. (Bei Excel ist dies die Funktion MEDIAN) Verteilung 9 8 Median = 14 7 6 5 Reihe2 4 3 2 1 29 27 25 23 21 19 17 15 13 11 9 7 5 3 1 0 Abbildung 122 : Median einer Messreihe 8-6 Modul 100 V1.2b.doc Abteilung Informatik/Technik Informationsbestände analysieren Statistik Kapitel 8 : Eigene Notizen © René Probst Jan 2004 8-7 Theorie 2 Modul 100 V1.2b.doc Modul-100 Abteilung Informatik/Technik