1. Deskriptive Statistik

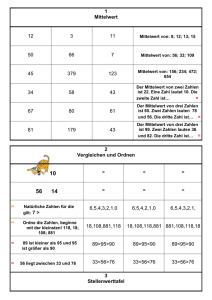
Einführung in Statistik Übungsaufgaben
Ü1
FH Campus Wien ITTBA, SS 2010
Übungsaufgaben zur Einführung in Statistik
1. Deskriptive Statistik
1.
Geben Sie zu nachstehenden Merkmalen den jeweils passenden Merkmalstyp an:
• Anzahl der Banküberfälle in einem Monat
• Berufskategorien in einem Unternehmen
• Feldstärke eines elektrischen Feldes
• Fertigungsstadien eines TV-Gerätes
• Körpergröße einer Person
• Schulnoten an einer Fachhochschule
• Systemzeit eines Rechners
• Tarifvarianten eines Internetproviders
• Wohnbevölkerung von Wien (laut letzter Volkszählung)
2.
Bestätigen Sie (an Hand der Daten aus dem Folder Straßenverkehrsunfälle 2004 – 2006)
die folgenden Aussagen:
Im Jahr 2006 forderte der Straßenverkehr im Durchschnitt ...
• alle 10 Minuten eine verunglückte Person,
• alle 17 Minuten eine verunglückte Person im Ortsgebiet,
• alle 24 Minuten eine verunglückte Person im Freiland,
• in 2,4 Stunden eine verunglückte Person durch Trunkenheit,
• in 2,4 Stunden ein verunglücktes Kind,
• in 12,0 Stunden eine getötete Person,
• ferner in 1,8 Tagen eine getötete Person im Ortsgebiet,
• in 6,5 Tagen eine getötete Person durch Trunkenheit,
• und in 15,9 Tagen ein getötetes Kind.
Das bedeutet täglich durchschnittlich rund 109 Unfälle mit Personenschaden, 142
Verletze und 2 Getötete.
3.
Die folgende Urliste enthält die Anzahl der Kinder von zwölf Familien:
2
4
1
1
3
2
1
1
2
1
2
5
Beschreiben Sie die Häufigkeitsverteilung dieser Stichprobe mittels einer Häufigkeitstabelle (absolute und relative Häufigkeiten) sowie eines Stab- und eines Kreisdiagramms.
4.
Die folgende Urliste enthält 23 Signalübertragungszeiten (in ms) in einem Netzwerk:
5,35
9,08
7,08
6,54
9,50
8,35
7,10
6,00
9,30
9,05
7,05
6,50
9,50
8,10
7,10
5,70
9,25
9,02
6,80 7,85
10,00 6,20
9,30
Einführung in Statistik Übungsaufgaben
Ü2
Nehmen Sie eine geeignete Klasseneinteilung zur Gruppierung des Datenmaterials vor,
stellen Sie eine Häufigkeitstabelle (mit Klassengrenzen, Klassenmitte, absoluten und
relativen Klassenhäufigkeiten) auf und zeichnen Sie das zugehörende Histogramm.
5.
Erstellen Sie eine Häufigkeitstabelle für die Unfallverletzten und Getöteten des Jahres
2006 nach Altersklassen (siehe Folder Straßenverkehrsunfälle 2004 – 2006) mit Klassengrenzen, Klassenmitte, absoluten und relativen Klassenhäufigkeiten sowie relativen
Summenhäufigkeiten, und vergleichen Sie die beiden Verteilungen durch eine geeignete
Grafik.
6.
Für die Kinderzahlen in Aufgabe 3 sowie für die Signalübertragungszeiten aus Aufgabe 4
ermittle man jeweils den kleinsten und größten Merkmalswert, den Modalwert, den
Median und die beiden p-Quantile xp für p = 1/3 und p = 2/3.
7.
Für die Kinderzahlen in Aufgabe 3 sowie für die Signalübertragungszeiten aus Aufgabe 4
ermittle man den Mittelwert x , die Standardabweichung s und den Variationskoeffizienten v. Wie groß ist jeweils der Anteil der Messwerte innerhalb der einfachen
Standardabweichung um den Mittelwert, welcher Anteil ist (im Fall einer normalverteilten Stichprobe) zu erwarten? Überprüfen Sie die Ergebnisse mit Excel.
8.
Aus den Altersklassendaten für die Unfallverletzten und Getöteten des Jahres 2006 (siehe
Folder Straßenverkehrsunfälle 2004 – 2006) berechne man jeweils das Durchschnittsalter
und die Standardabweichung.
9.
Aus den Daten für die Bevölkerung im Jahresdurchschnitt nach Altersklassen des Jahres
2006 (siehe Folder Straßenverkehrsunfälle 2004 – 2006) berechne man
(a) Mittelwert, Median und modale Klasse sowie
(b) Varianz, Standardabweichung und Schiefe
für das Alter der österreichischen Bevölkerung.
10. Berechnen Sie für die Signalübertragungszeiten in Aufgabe 4 den Median ~
x , das erste
und das dritte Quartil Q1 und Q3 sowie den Interquartilabstand IQR, und veranschaulichen Sie die Ergebnisse durch einen Box-Plot.
11. Man vergleiche die Erträge zweier Getreidesorten an Hand der entsprechenden BoxPlots.
Laufnummer
1
2
3
4
5
6
7
8
9
10
Getreideerträge (in 100 kg/ha)
Sorte A
Sorte B
29,5
30,2
37,3
37,8
36,1
35,9
31,0
31,2
37,2
36,5
35,2
37,4
34,1
34,1
34,1
35,2
36,7
37,1
35,2
36,6
Einführung in Statistik Übungsaufgaben
Ü3
12. Berechnen Sie das Unfallrisiko auf Österreichs Straßen, indem Sie die Zahlen der
Verletzten bzw. Getöteten des Jahres 2006 nach Altersklassen auf die jeweiligen
Bevölkerungszahlen im Jahresdurchschnitt beziehen (siehe Folder Straßenverkehrsunfälle 2004 – 2006), und vergleichen Sie die beiden Verteilungen durch ihre Boxplots.
13. Man konstruiere eine Stichprobe, für welche
(a) der Mittelwert größer (bzw. kleiner) als der Median ist,
(b) der Modalwert größer (bzw. kleiner) als der Mittelwert ist.
Wie beeinflussen einzelne Merkmalswerte den Mittelwert, den Median bzw. den Modalwert?
(c) Ferner gebe man zwei Stichproben an, welche denselben Mittelwert, aber unterschiedliche Varianzen besitzen.
14. Man beweise, dass sich die Verschiebung einer Stichprobe zwar auf den Mittelwert,
jedoch nicht auf die Varianz auswirkt.
Anleitung: Zu einer Variablen X mit den Werten xi, i = 1,...,n, betrachte man die Variable
Y mit yi = xi + d, i = 1,...,n, und bestimme deren Mittel y bzw. Varianz sy2.
15. Beim Qualitätsvergleich von Äpfeln wurden 550 Äpfel der Sorte Jonathan und 760 Äpfel
der Sorte Krummstiel untersucht. Dabei wurden im ersten Fall 190, im zweiten Fall 210
wurmige Äpfel gezählt. Man stelle diese Ergebnisse in einer Vierfeldertafel zusammen
(absolute und relative Häufigkeiten sowie alle Randhäufigkeiten). Haben Sie den
Eindruck, dass sich die Anteile der wurmigen Äpfel in den beiden Sorten voneinander
unterscheiden?
16. Eine Studie über die Rauchgewohnheiten von männlichen und weiblichen Jugendlichen
im Schweizer Kanton Zürich weist folgende Zahlen aus:
Anzahl der
Zigaretten pro Tag
keine
1-2
3-7
8 - 14
15 - 21
> 21
gesamt
Burschen
Mädchen
2058
122
251
311
544
293
3579
1304
133
241
266
259
93
2296
Man untersuche die Frage, ob die Studie auf einen signifikanten Unterschied in den
Rauchgewohnheiten zwischen männlichen und weiblichen Jugendlichen hinweist. Zu
diesem Zweck vergleiche man die tatsächlich beobachteten Häufigkeiten mit jenen
erwarteten Werten, welche sich im Fall der Unabhängigkeit der beiden Merkmale
Zigarettenkonsum und Geschlecht ergeben würden.
17. Acht Ehepaare wurden in einem psychologischen Test auf ihre Einstellung zum
Computer untersucht. Dabei wurden die folgenden Testscores erreicht (hohe Werte
bedeuten eine positive Einstellung zum Computer):
Paar
Mann
Frau
1
107
110
2
105
107
3
101
103
4
96
95
5
91
90
6
97
97
7
105
108
8
94
92
Einführung in Statistik Übungsaufgaben
Ü4
Man bestimme die Güte des linearen Zusammenhangs zwischen den Einstellungen der
Ehepartner durch den Korrelationskoeffizienten rXY der Stichprobe.
18. Im vorhergehenden Beispiel beantworte man die Frage, wie ähnlich sich die Ehepaare
bezüglich ihrer Einstellung zum Computer sind, indem man für beide Testreihen die
Rangzahlen ermittelt und daraus den Spearmanschen Rangkorrelationskoeffizienten
berechnet.
19. Wie sehen die Streudiagramme für zwei metrische Merkmale X und Y aus, die (a) stark
bzw. schwach positiv korrelieren, (b) stark bzw. schwach negativ korrelieren, (c) nicht
korrelieren. Geben Sie jeweils ein Beispiel an.
20. Die folgende Tabelle zeigt, wie die Stückkosten eines bestimmten elektronischen Bauteils von der Menge abhängen:
Menge x (in 100)
Stückkosten y (in €)
1
2
120 90
6
75
9
45
12
30
Man ermittle die Regressionsgerade y = a + bx und skizziere die Wertepaare sowie die
Regressionsgerade in einem Streudiagramm. Welche Stückkosten sind bei einer Menge
von 250 Stück zu erwarten? Bei welcher Menge betragen die Stückkosten 50 €? Lässt
sich die Regression durch ein nichtlineares Modell verbessern?
21. Der Luftdruck p (in hPa) nimmt mit zunehmender Höhe h (in km) über dem Meeresspiegel gemäß der sogenannten barometrischen Höhenformel ab:
p = a e−bh .
Man berechne mit Hilfe der Regressionsrechnung eine Näherung für die Werte von a und
b aus nachstehender Tabelle.
Höhe h (in km)
Luftdruck p (in hPa)
0
1013
1
899
2
795
3
701
4
616
5
540
Anleitung: Führen Sie eine lineare Regression zwischen der Höhe h und dem logarithmierten Luftdruck ln p durch.