Allgemeiner Mittelwert - Paul-Ehrlich

Gemeinsame Definition der wichtigsten Mittelwerte
Arithmetischer Mittelwert:
Hier sucht man eine Zahl 𝑚, für die gilt:
𝑥1 + 𝑥2 + ⋯ + 𝑥𝑛 = 𝑚 + 𝑚 + ⋯ + 𝑚 = 𝑛 ∙ 𝑚 ⟹ 𝑚 =
𝑥1 +𝑥2 +⋯+𝑥𝑛
𝑛
Geometrischer Mittelwert:
= 𝑥̅
Hier sucht man eine Zahl 𝑚, für die gilt:
𝑥1 ∙ 𝑥2 ∙ ⋯ ∙ 𝑥𝑛 = 𝑚 ∙ 𝑚 ∙ … ∙ 𝑚 = 𝑚𝑛 ⟹ 𝑚 = 𝑛�𝑥1 ∙ 𝑥2 ∙ ⋯ ∙ 𝑥𝑛 = 𝑥̅𝐺
Harmonischer Mittelwert:
Hier sucht man eine Zahl 𝑚, für die gilt:
1
𝑥1
+
1
𝑥2
+ ⋯+
1
𝑥𝑛
=
1
𝑚
+
1
𝑚
+ ⋯+
Quadratischer Mittelwert:
1
𝑚
=𝑛∙
1
𝑚
⟹𝑚=
𝑛
1
1
1
+ +⋯+
𝑥1 𝑥2
𝑥𝑛
Hier sucht man eine Zahl 𝑚, für die gilt:
= 𝑥̅𝐻
𝑥1 2 + 𝑥2 2 + ⋯ + 𝑥𝑛 2 = 𝑚2 + 𝑚2 + ⋯ + 𝑚2 = 𝑛 ∙ 𝑚2 ⟹ 𝑚 = �
𝑥1 2 +𝑥2 2 +⋯+𝑥𝑛 2
𝑛
= 𝑥̅𝑄
Ein Verallgemeinerter Mittelwert
(Hölder1-Mittel, the generalized mean, p-th power-mean)
𝑛
1
𝑝
1 𝑝
1
𝑝
𝑝
𝑝
𝑀𝑝 = � �𝑥1 + 𝑥2 + ⋯ + 𝑥𝑛 � = � ∙ � 𝑥𝑖 � 𝑚𝑖𝑡 𝑝 ≠ 0, 𝑥𝑖 ≥ 0
𝑛
𝑛
𝑝
Spezialfälle:
• 𝑝 → −∞ ⟹ 𝑀𝑝 = 𝑥𝑚𝑖𝑛 (Minimum)
• 𝑝 = −1 ⟹ 𝑀𝑝 = 𝑥̅𝐻
(Harmonisches Mittel)
• 𝑝=2
(Quadratisches Mittel)
• 𝑝→0
• 𝑝=1
• 𝑝=3
1
𝑖=1
⟹ 𝑀𝑝 = 𝑥̅𝐺
⟹ 𝑀𝑝 = 𝑥̅
⟹ 𝑀𝑝 = 𝑥̅𝑄
⟹ 𝑀𝑝 = 𝑥̅𝐾
(Geometrisches Mittel)
(Arithmetisches Mittel)
(Kubisches Mittel)
• 𝑝 → ∞ ⟹ 𝑀𝑝 = 𝑥𝑚𝑎𝑥 (Maximum)
Otto Ludwig Hölder (* 22. Dezember 1859 in Stuttgart; † 29. August 1937 in Leipzig) war ein deutscher Mathematiker
Veranschaulichung des Hölder-Mittels an einem Beispiel (Excel-Tabelle)
xi
1
5
1
6
1
generalized
p
mean
-100
1,005121
1 =MIN(xi)
-1
1,485149 1,485149 =HARMITTEL(xi)
0,000001
1,974351
1,97435 =GEOMITTEL(xi)
1
2,8
2,8 =MITTELWERT(xi)
2
3,577709 3,577709 =WURZEL(QUADRATESUMME(xi)
3
4,097599
/ANZAHL(xi))
100
5,904207
6 =MAX(xi)
{=(SUMME(xi^A8)/ANZAHL(xi))^(1/A8)}
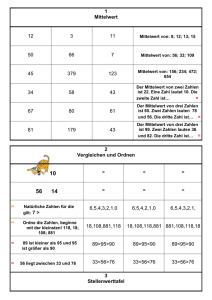
Das obige Beispiel zeigt, dass z. B. die Zahlen 1, 5, 1, 6, 1 (hier interpretiert als Schulnoten) je nach Wahl des
Mittelwerts bei ganzzahliger Rundung zu vier verschiedenen Durchschnittsnoten führen können:
• Quadratisches Mittel: 3,57.. ≈ Note 4
• Arithmetisches Mittel: 2,8
≈ Note 3
• Geometrisches Mittel: 1,97.. ≈ Note 2
• Harmonisches Mittel: 1,48.. ≈ Note 1
Es dürfte klar sein, welchen Mittelwert die Schüler/innen bevorzugen würden!