Formelsammlung als PDF herunterladen
Werbung
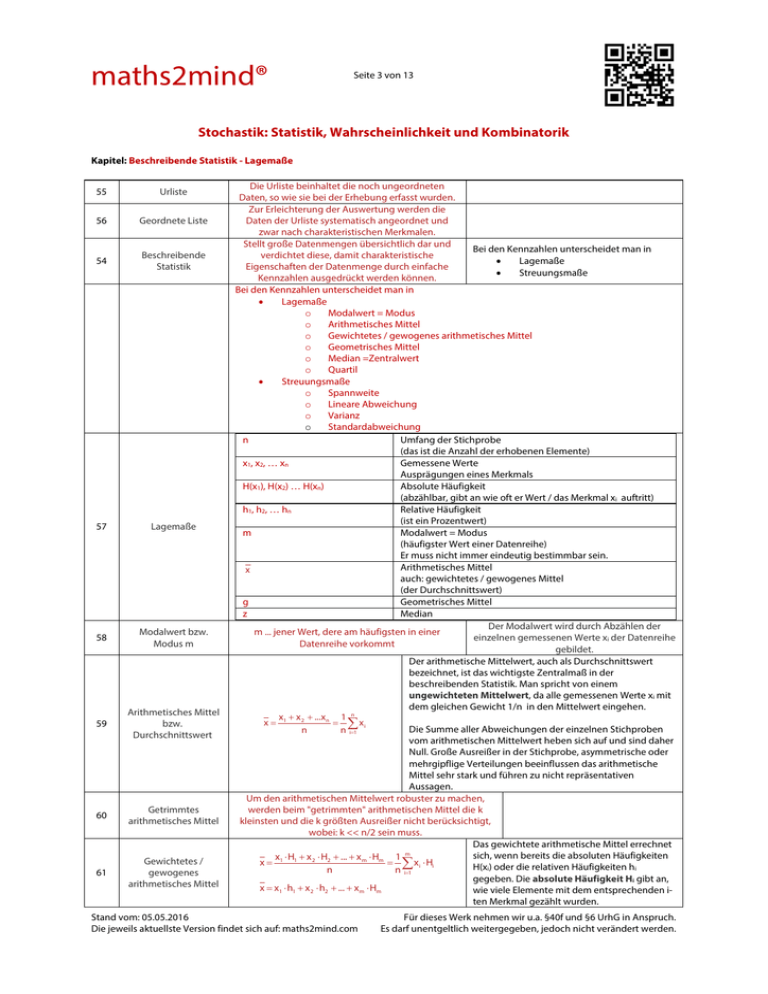
maths2mind® Seite 3 von 13 Stochastik: Statistik, Wahrscheinlichkeit und Kombinatorik Kapitel: Beschreibende Statistik - Lagemaße 55 Urliste 56 Geordnete Liste 54 Beschreibende Statistik 57 Lagemaße 58 Modalwert bzw. Modus m 59 Arithmetisches Mittel bzw. Durchschnittswert 60 Getrimmtes arithmetisches Mittel 61 Gewichtetes / gewogenes arithmetisches Mittel Die Urliste beinhaltet die noch ungeordneten Daten, so wie sie bei der Erhebung erfasst wurden. Zur Erleichterung der Auswertung werden die Daten der Urliste systematisch angeordnet und zwar nach charakteristischen Merkmalen. Stellt große Datenmengen übersichtlich dar und Bei den Kennzahlen unterscheidet man in verdichtet diese, damit charakteristische Lagemaße Eigenschaften der Datenmenge durch einfache Streuungsmaße Kennzahlen ausgedrückt werden können. Bei den Kennzahlen unterscheidet man in Lagemaße o Modalwert = Modus o Arithmetisches Mittel o Gewichtetes / gewogenes arithmetisches Mittel o Geometrisches Mittel o Median =Zentralwert o Quartil Streuungsmaße o Spannweite o Lineare Abweichung o Varianz o Standardabweichung n Umfang der Stichprobe (das ist die Anzahl der erhobenen Elemente) x1, x2, … xn Gemessene Werte Ausprägungen eines Merkmals H(x1), H(x2) … H(xn) Absolute Häufigkeit (abzählbar, gibt an wie oft er Wert / das Merkmal xi auftritt) h1 , h2 , … hn Relative Häufigkeit (ist ein Prozentwert) m Modalwert = Modus (häufigster Wert einer Datenreihe) Er muss nicht immer eindeutig bestimmbar sein. Arithmetisches Mittel x auch: gewichtetes / gewogenes Mittel (der Durchschnittswert) g Geometrisches Mittel z Median Der Modalwert wird durch Abzählen der m ... jener Wert, dere am häufigsten in einer einzelnen gemessenen Werte xi der Datenreihe Datenreihe vorkommt gebildet. Der arithmetische Mittelwert, auch als Durchschnittswert bezeichnet, ist das wichtigste Zentralmaß in der beschreibenden Statistik. Man spricht von einem ungewichteten Mittelwert, da alle gemessenen Werte xi mit dem gleichen Gewicht 1/n in den Mittelwert eingehen. n x x ...x n 1 x 1 2 xi Die Summe aller Abweichungen der einzelnen Stichproben n n i1 vom arithmetischen Mittelwert heben sich auf und sind daher Null. Große Ausreißer in der Stichprobe, asymmetrische oder mehrgipflige Verteilungen beeinflussen das arithmetische Mittel sehr stark und führen zu nicht repräsentativen Aussagen. Um den arithmetischen Mittelwert robuster zu machen, werden beim "getrimmten" arithmetischen Mittel die k kleinsten und die k größten Ausreißer nicht berücksichtigt, wobei: k << n/2 sein muss. Das gewichtete arithmetische Mittel errechnet sich, wenn bereits die absoluten Häufigkeiten x1 H1 x 2 H2 ... x m Hm 1 m xi Hi x H(xi) oder die relativen Häufigkeiten hi n n i1 gegeben. Die absolute Häufigkeit Hi gibt an, x x1 h1 x 2 h2 ... xm Hm wie viele Elemente mit dem entsprechenden iten Merkmal gezählt wurden. Stand vom: 05.05.2016 Die jeweils aktuellste Version findet sich auf: maths2mind.com Für dieses Werk nehmen wir u.a. §40f und §6 UrhG in Anspruch. Es darf unentgeltlich weitergegeben, jedoch nicht verändert werden. maths2mind® Seite 4 von 13 Stochastik: Statistik, Wahrscheinlichkeit und Kombinatorik Kapitel: Beschreibende Statistik - Lagemaße 62 Geometrische Mittel g n x 1 x 2 ... x n 63 Median bzw. Zentralwert Der Median ist der in der Mitte stehende Wert xi einer nach aufsteigender Größe geordneten Liste. Es wird vorwiegend in den Finanz- und Wirtschaftswissenschaften für Wachstumsfaktoren eingesetzt. Man bildet das Produkt der n Stichproben und zieht anschließend die n-te Wurzel. Keiner der gemessenen Werte darf Null oder Negativ sein. 64 Quartilen Quartilen teilen eine nach aufsteigender Größe geordnete Liste in 4 Viertel. Stand vom: 05.05.2016 Die jeweils aktuellste Version findet sich auf: maths2mind.com Das 1. Quartil q1 ist der Median der unteren Hälfte. Das 2. Quartil q2=z ist der Median selbst Das 3. Quartil q3 ist der Median der oberen Hälfte. Für dieses Werk nehmen wir u.a. §40f und §6 UrhG in Anspruch. Es darf unentgeltlich weitergegeben, jedoch nicht verändert werden.