Gerechtigkeit bei der Spiele AG? – Median, Modus, Boxplot
Werbung
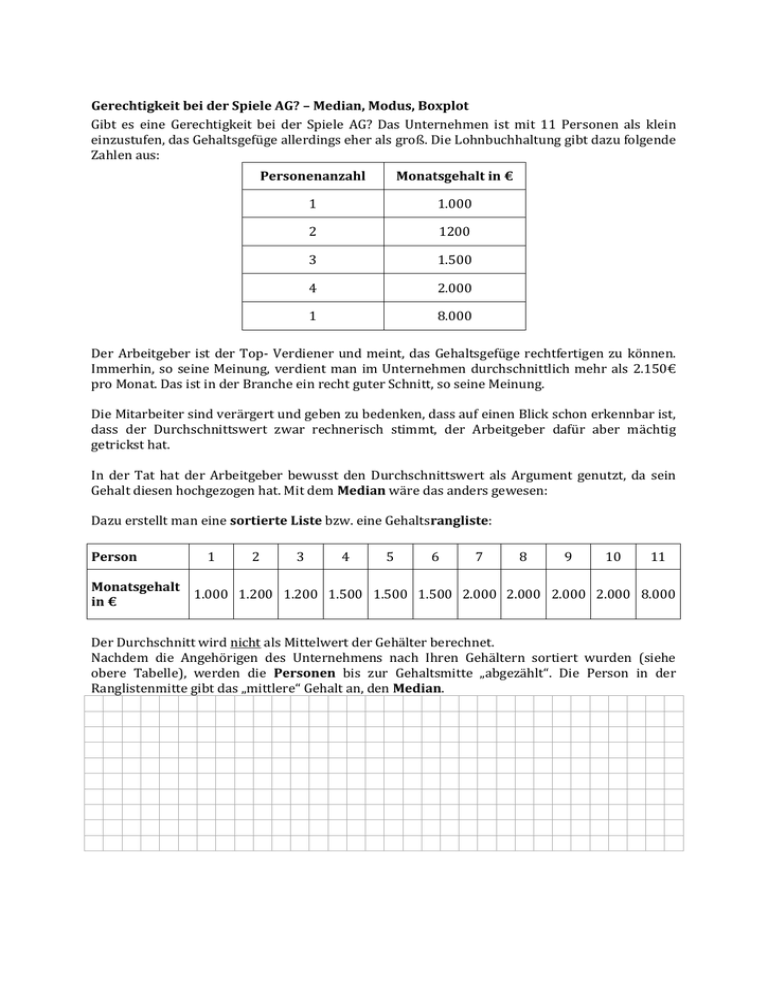
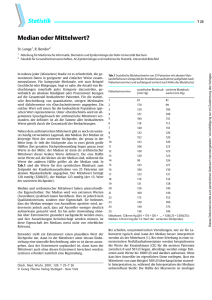
Gerechtigkeit bei der Spiele AG? – Median, Modus, Boxplot Gibt es eine Gerechtigkeit bei der Spiele AG? Das Unternehmen ist mit 11 Personen als klein einzustufen, das Gehaltsgefüge allerdings eher als groß. Die Lohnbuchhaltung gibt dazu folgende Zahlen aus: Personenanzahl Monatsgehalt in € 1 1.000 2 1200 3 1.500 4 2.000 1 8.000 Der Arbeitgeber ist der Top- Verdiener und meint, das Gehaltsgefüge rechtfertigen zu können. Immerhin, so seine Meinung, verdient man im Unternehmen durchschnittlich mehr als 2.150€ pro Monat. Das ist in der Branche ein recht guter Schnitt, so seine Meinung. Die Mitarbeiter sind verärgert und geben zu bedenken, dass auf einen Blick schon erkennbar ist, dass der Durchschnittswert zwar rechnerisch stimmt, der Arbeitgeber dafür aber mächtig getrickst hat. In der Tat hat der Arbeitgeber bewusst den Durchschnittswert als Argument genutzt, da sein Gehalt diesen hochgezogen hat. Mit dem Median wäre das anders gewesen: Dazu erstellt man eine sortierte Liste bzw. eine Gehaltsrangliste: Person 1 2 3 4 5 6 7 8 9 10 11 Monatsgehalt 1.000 1.200 1.200 1.500 1.500 1.500 2.000 2.000 2.000 2.000 8.000 in € Der Durchschnitt wird nicht als Mittelwert der Gehälter berechnet. Nachdem die Angehörigen des Unternehmens nach Ihren Gehältern sortiert wurden (siehe obere Tabelle), werden die Personen bis zur Gehaltsmitte „abgezählt“. Die Person in der Ranglistenmitte gibt das „mittlere“ Gehalt an, den Median. Nochmal zur Veranschaulichung des Medians: Den Arbeitnehmern der Spiele AG sollte klar werden, dass „Ausreißer“ wie das Gehalt des Arbeitgebers beim Median weniger Berücksichtigung findet. Zudem: Betrachtet man nur das Gehalt der Arbeitnehmer, fällt auch der arithmetischen Mittelwert deutlich geringer aus. Übrigens der Median des Gehalts bei 10 Arbeitnehmern wird berechnet, indem das Gehalt der 5. und 6. Person gemittelt wird. Berechnung des arithmetischen Mittelwertes und des Median bei 10 Arbeitnehmern: Für eine geeignete Veranschaulichung mit dem Median werden Boxplots verwendet (siehe unten). In einem Boxplot wird aufgelistet, was der Mindest- als auch der Höchstverdienst ist, der Median wird aufgeführt sowie auch die Quartile. Bei 10 Personen betrachtet man beim 1. Quartil nur die 5 Personen der ersten Hälfte und berechnet dann den Median für dieses Intervall. Bei 11 Personen lässt man die 6. Person aus und betrachtet ebenso nur die ersten fünf Personen. Beim 3.Quartil ist die Überlegung völlig gleich: bei insgesamt 10 Personen betrachtet man die letzten 5 Personen. Bei 11 Personen wird die sechste Person vernachlässigt; es werden die letzten 5 Personen in Betracht gezogen und dann der Median berechnet. Das Boxplot für den Fall, dass das Gehalt aller 11 Personen betrachtet wird: Boxplot für 10 Personen (ohne Arbeitgeber): Im Übrigen: Der Modus, das ist der Wert, der am häufigsten aufgelistet wird, liegt bei der Spiele AG (11 Personen) bei einem Monatsgehalt von 2.000€. Aufgabe 1 Bei Tarifverhandlungen nimmt die Gewerkschaft „Gute Arbeit“ für ihre Argumentation bei Tarifverhandlungen gerne folgende Tabelle: Monatseinkommen Anzahl 2.000 EUR 70 3.000 EUR 20 5.000 EUR 8 8.000 EUR 2 a) Berechnen Sie die relativen Häufigkeiten, den (arithmetischen) Mittelwert und die Standardabweichung. Nutzen Sie dazu die leeren Spalten der Tabelle! b) Bestimmen Sie den Median. c) Geben Sie der Gewerkschaft mit Hilfe der Tabelle ein Argument für die Tarifverhandlungen an die Hand. d) Beschreiben Sie die Veränderung des Mittelwertes und die des Median, wenn die beiden Topverdiener (bisher 8.000€/ Monat) nun 10.000€ im Monat verdienen würden. Aufgabe 2 Die Geschäftsleitung der Spiele AG möchte die Verkaufsstrategie des Unternehmens ändern und zieht zur Analyse die Verkaufszahlen aller Produkte zu Rate. Entsprechende Informationen sind dem folgenden Schaubild zu entnehmen: Verkaufszahlen 1800 1600 1400 1200 1380 1440 1400 2007 2008 2009 1510 1520 2010 2011 1600 1600 1510 1420 1100 1000 800 600 400 200 0 2000 2012 2013 2014 2015 a) Berechnen Sie das arithmetische Mittel als auch die Standardabweichung! Nutzen Sie dazu die vorgegebene Tabelle! b) Bestimmen Sie den Median und die Quartile und zeichnen Sie dazu ein Boxplot! c) Begründen Sie den (größeren) Unterschied des berechneten Mittelwertes zum Median. Aufgabe 3 In einem Industriebetrieb werden Drahtstift der Länge 100 mm produziert. Aufgrund von Kundenreklamationen wurden vor und nach der Nachjustierung der Maschine je eine Stichprobe genommen, bei der 1000 Drahtstifte auf ihre Länge hin untersucht wurden. Die Werte vor der Nachjustierung können Sie der folgenden Tabelle entnehmen: Länge Absolute Relative Häufigkeit Häufigkeit xi in ki hi mm 95 18 96 42 97 104 98 122 99 161 100 197 101 96 102 30 103 90 104 140 Summe a) Vervollständigen Sie die Tabelle und berechnen Sie den (arithmetischen) Mittelwert, die Standardabweichung und die Varianz. b) Aufgrund von Messungenauigkeiten im Bereich bis 96 mm stellte man erst später fest, dass 5 von den 18 Drahtstiften nicht 95 mm sondern lediglich 93 mm lang waren. Beschreiben Sie die Auswirkung auf den (arithmetischen) Mittelwert als auch auf den Median! c) Bei der Stichprobe nach der Nachjustierung wurden folgende Werte ermittelt: Mittelwert: 100,03 mm Varianz: 1,7891 mm² Standardabweichung: ca. 1,34 mm Vergleichen Sie die beiden Stichproben (aus a) und c)) und beurteilen Sie, ob die Nachjustierung ein Erfolg war.