Formelsammlung Ma 2.1
Werbung
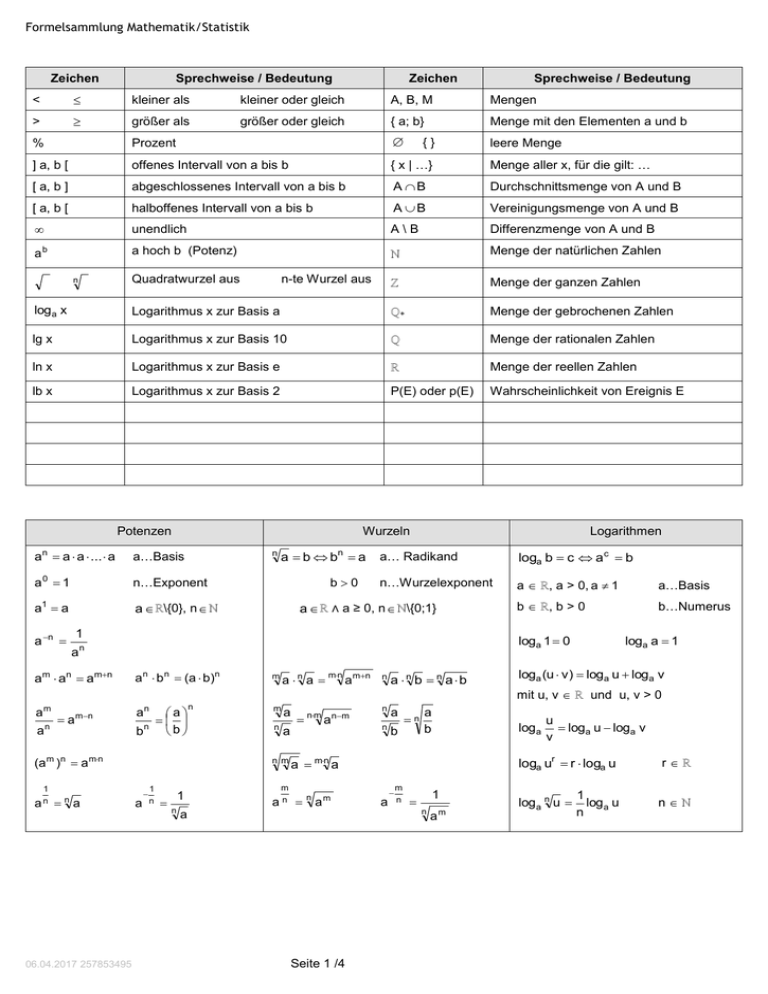
Formelsammlung Mathematik/Statistik
Zeichen
Sprechweise / Bedeutung
Zeichen
Sprechweise / Bedeutung
<
kleiner als
kleiner oder gleich
A, B, M
Mengen
>
größer als
größer oder gleich
{ a; b}
Menge mit den Elementen a und b
leere Menge
%
Prozent
] a, b [
offenes Intervall von a bis b
{ x | …}
Menge aller x, für die gilt: …
[ a, b ]
abgeschlossenes Intervall von a bis b
A B
Durchschnittsmenge von A und B
[ a, b [
halboffenes Intervall von a bis b
A B
Vereinigungsmenge von A und B
unendlich
A\B
Differenzmenge von A und B
ab
a hoch b (Potenz)
ℕ
Menge der natürlichen Zahlen
ℤ
Menge der ganzen Zahlen
Quadratwurzel aus
n
n-te Wurzel aus
{}
log a x
Logarithmus x zur Basis a
ℚ+
Menge der gebrochenen Zahlen
lg x
Logarithmus x zur Basis 10
ℚ
Menge der rationalen Zahlen
ln x
Logarithmus x zur Basis e
ℝ
Menge der reellen Zahlen
lb x
Logarithmus x zur Basis 2
P(E) oder p(E)
Wahrscheinlichkeit von Ereignis E
Potenzen
Wurzeln
an a a ... a
a…Basis
a0 1
n…Exponent
a1 a
a ℝ\{0}, n ℕ
a n
n
b0
a… Radikand
loga b c a c b
n…Wurzelexponent
a ℝ, a > 0, a 1
a…Basis
b ℝ, b > 0
b…Numerus
a ℝ ∧ a ≥ 0, n ℕ\{0;1}
1
loga 1 0
an
am an amn
a n b n (a b ) n
am
a
n
b
b
an
a b bn a
Logarithmen
a mn
an
(a m )n a mn
06.04.2017 257853495
a n a mn a mn
n
a n b n ab
m
a
n
a
n
a
nm
1
an n a
n
m
a
1
n
1
n
nm a nm
a
n
n
b
b
m
a n n am
a
Seite 1 /4
a
m
n
1
n
loga (u v ) loga u loga v
mit u, v ℝ und u, v > 0
loga
a mn a
a
m
loga a 1
u
loga u loga v
v
loga ur r loga u
rℝ
1
log a u
n
nℕ
log a n u
Formelsammlung Mathematik/Statistik
Quadratische Gleichungen
allgemeine Form
Gleichung
ax 2 bx c 0
Lösungen
x1,2
Diskriminante
D b 4ac
Normalform
x 2 px q 0
p
p
q
2
2
a,b,c,p,q ℝ;
2
a,b,c,p,q sind Konstanten
2
b b 2 4ac
2a
x 1,2
p
D q
2
2
Lösung in ℝ
D>0
L = {x1; x2}
D=0
L = {x1} = {x2}
D<0
L=∅
a0
Statistik
Lage– und Streumaße
Modalwert (Modus)
Häufigster Wert unter den Ergebnissen einer Stichprobe
Mittelwert (arithmetisches Mittel) x
x
Zentralwert (Median) z
n ist ungerade:
x1 x 2 ... x n 1 n
xi
n
n i1
z x n1
2
n ist gerade:
Spannweite (Streu- oder Variationsbreite) R
Mittlere Abweichung vom Zentralwert z bei
einer Stichprobe vom Umfang n
06.04.2017 257853495
z
1
(x n x n )
1
2 2
2
R x max x min
1
1 n
( x1 z x 2 z ... x n z ) x i z
n
n i1
Seite 2 /4
Formelsammlung Mathematik/Statistik
Wahrscheinlichkeitsrechnung
Grundlegende Begriffe
Zufallsversuch
Versuch mit mehreren möglichen Ergebnissen 1, 2 ,...,n
Ergebnismenge (Stichprobenraum)
Menge aller möglichen Ergebnisse {1, 2 ,...,n }
Ereignis E
Teilmenge der Ergebnismenge
sicheres Ereignis
Ereignis, das bei jeder Versuchsdurchführung eintritt
unmögliches Ereignis
Ereignis, das bei keiner Versuchsdurchführung eintritt
Elementarereignis {a}
Ereignis mit nur einem Element
Gegenereignis E
Komplementärmenge von E
absolute Häufigkeit Hn (E) des Eintretens von E
Anzahl des Eintretens von E bei n
E
Versuchsdurchführungen
relative Häufigkeit hn (E) des Eintretens von E
hn
Hn (E)
n
Klassische Wahrscheinlichkeit
–
Jedes von endlich vielen Elementarereignissen E
hat die gleiche Chance zum Auftreten, kein
Elementarereignis ist unmöglich.
–
P(E)
Anzahl der für E günstigen Ergebnisse
Anzahl der möglichen Ergebnisse
Das Auftreten eines Elementarereignisses schließt
das gleichzeitige Auftreten eines anderen
Elementarereignisses aus.
Regeln und Sätze für das Rechnen mit Wahrscheinlichkeiten
0 P(E) 1
für E = {a1, a2, … , ak} gilt
Summenregel
P(E) = P({a1}) + P({a2}) + … + P({ak})
P() 1
Wahrscheinlichkeit des sicheren Ereignisses
P() 1
Wahrscheinlichkeit des unmöglichen Ereignisses
P(E) 1 P(E)
Wahrscheinlichkeit des Gegenereignisses
P(E1 E2 ) P(E1 ) P(E2 ) P(E1 E2 )
Additionssatz für zwei Ereignisse
Pfadregel
Produktregel:
Die Wahrscheinlichkeit eines Elementarereignisses ist gleich dem Produkt der Wahrscheinlichkeiten
entlang des zugehörigen Pfades (Pfadwahrscheinlichkeit).
Summenregel: Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe aller Pfadwahrscheinlichkeiten seiner
zugehörigen Elementarereignisse.
06.04.2017 257853495
Seite 3 /4
Formelsammlung Mathematik/Statistik
Kombinatorik
Binomialkoeffizienten
n n (n 1) (n 2) ... n k 1
n!
1 2 3 . . . k
k ! n k !
k
Permutation
Jede mögliche Anordnung von n Elementen, in der alle Elemente verwendet werden
Anzahl von Permutationen
ohne Wiederholung
von n verschiedenen Elementen
Pn n!
mit Wiederholung
von n Elementen mit k Klassen von untereinander gleichen Elementen.
Die Klassen enthalten n1, n2, … , nk Elemente.
Pn
n!
n1!n2 !... nk !
Variationen
Jede mögliche Anordnung (mit Berücksichtigung der Reihenfolge) aus je k von n
von n Elementen zur k-ten Klasse
Elementen
Anzahl von Variationen k-ter Klasse
von n verschiedenen Elementen
ohne Wiederholung
von n verschiedenen Elementen
mit Wiederholung
Vnk
n!
(n k )!
Vnk nk
Kombinationen
Jede mögliche Anordnung (ohne Berücksichtigung der Reihenfolge) aus je k von n
von n Elementen zur k-ten Klasse
Elementen
Anzahl von Kombinationen k-ter Klasse
von n verschiedenen Elementen
ohne Wiederholung
von n verschiedenen Elementen
mit Wiederholung
06.04.2017 257853495
Ckn
n
n!
(n k )! k! k
n k 1
Ckn
k
Seite 4 /4


