Script vom 7.3.2006
Werbung

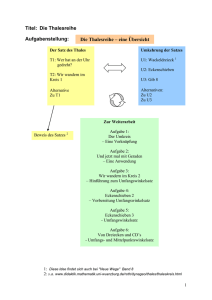
Staatliches Schulamt für den Landkreis Marburg-Biedenkopf Anwendung der dynamischen Geometriesoftware „Euklid“ Dienstag, 07.03.2006, 13:30 Uhr – 15:00 Uhr und 15:20 Uhr – 16:50 Uhr Elisabethschule Marburg Matthias Grasse, Hadamar [email protected] Dieses Script und alle Beispiele finden Sie unter: http://www.fjls.de/265.0.html 1. Zeitplan 1 Übersicht über die UR-Reihe 5. Schuljahr zu „Geometrie“ 2 Übersicht über die UR-Reihe 7. Schuljahr zu „Dreieckskonstruktionen“ 3 Interessante Links zu Euklid-Dynageo 4 Ausblick/Zukunft 5 Rückblick auf den Workshop 2 Einsatz von Euklid Dynageo im Unterricht 2.1 Eine Einführung für das 5. Schuljahr 2.1.1 Lehrplaninhalte Der Lehrplan –Bildungsgang Gymnasium/Realschule- sieht für das 5. Schuljahr das Themengebiet „Geometrie“ vor. (Stundenumfang 40 Std.) Räumliche Grundformen Geometrische Körper, Volumen und Oberflächeninhalt von Quadern und Würfeln Ebene Grundformen Ebene Figuren, Koordinatensystem, Flächeninhalt und Umfang von Rechtecken und Quadraten Geometrische Grundbegriffe (Punkt, Strecke, Fläche, …) Lagebeziehung von Geraden Arbeitsmethoden der Schülerinnen und Schüler: Handelnde zeichnerische Aktivitäten stehen im Vordergrund 2.1.2 Möglicher Einstieg in das Programm a) Folgende Übungen könnten zum ersten Kontakt mit dem Programm dienen: - punkte.geo [2], flaechen.geo [2], dreieck.geo [2], 4cm.geo [2], vieleck.geo [2] Spielen Sie ruhig ein wenig herum mit den Dateien. Geometrie kann richtig Spaß machen! Auf eine genauere didaktisch-methodische Kommentierung wird verzichtet, da es sich beim Teilnehmerkreis fast ausnahmslos um erfahrene Mathematiklehrer handelt. 2/12 b) Weitere einführende Übungen - Übungen zu Vielecken und deren Umfang - mathe heute, S. 103, Nr. 13 (*.geo-Datei vorhanden) - mathe heute, S. 108, Nr. 5 (*.geo-Datei vorhanden) c) Arbeit an neuen Inhalten - Schrägbilder von Körpern - mathe heute, S. 130, Nr. 14 b) (*.geo-Datei vorhanden) - Geradenspiegelung - drei Arbeitsblätter (Spiegelung1.geo – Spiegelung3.geo) 3/12 - Verschiebung - Datei: Verschiebung.geo Bei diesem dynamischen Arbeitsblatt kann die Originalfigur (Dreieck ABC) und der Verschiebungspfeil PQ verändert werden. Durch einen Mitschüler soll nun das Bild (Dreieck A’B’C’) „zurechtgeschoben“ werden. Die Kontrolle erfolgt durch das Ziehen am LÖSUNGSPUNKT: Der Sachverhalt ist hier absichtlich fehlerhaft dargestellt, dass man das richtige Bilddreieck (dünne Linien) erkenn. 4/12 Vorgehen zur Konstruktion: 1. Konstruktion der zwei Dreiecke (ABC und A’B’C’), diese sind völlig unabhängig! 2. Färbung nach Wunsch. 3. Konstruktion des Verschiebungspfeils PQ. 4. Konstruktion von Parallelen zu PQ durch alle Originalpunkte 5. Einblendung/ Messung der Länge des Verschiebungspfeils PQ 6. Konstruktion der Lösungsstrecke mit festen Punkten von 2 cm Länge 7. Festlegung eines beweglichen Punktes auf dieser Strecke 8. Messung der Länge vom linken Anfangspunkt der Lösungsstrecke bis zum bewegl. Punkt 9. Ausblenden des Anfangs- und Endpunktes der Lösungstrecke 10. Konstruktion von Kreisen um alle Originalpunkte mit dem Radius: (Länge von PQ / 2) * Länge der (veränderlichen) Lösungstrecke 11. Festlegung der Schnittpunkte der variablen Kreise mit den Parallelen 12. Verbinden der drei Schnittpunkte Der Rest ist Kosmetik. Hier alle verdeckten Linien: - zusammenfassende Übungen - drei zunächst völlig gleich aussehende Dateien haben es in sich! (Dateien aufgabe1.geo – aufgabe3.geo) unbedingt ansehen! 5/12 2.2. Eine Einführung für das 7. Schuljahr 2.2.1 Lehrplaninhalte Der Lehrplan –Bildungsgang Gymnasium/Realschule- sieht für das 7. Schuljahr das Themengebiet „Dreieckskonstruktionen“ vor. (Stundenumfang 24 Std.) Wesentliche Inhalte: o Winkel an Geradenkreuzungen o Winkelsumme im Dreieck o Klassifizierung in Dreiecksformen, Eigenschaften der Dreiecksformen o Höhe o Kongruente Figuren – Kongruenzsätze o Einfache Dreieckskonstruktionen nach vorgegebenen Maßen mit Planfigur und Konstruktionsbeschreibung o Konstruktion von Mittelsenkrechte (Umkreis), Winkelhalbierende (Inkreis), Seitenhalbierende (Schwerpunkt) o Satz des Thales o Fakultativ: Einsatz dynamischer Geometriesoftware 2.2.2 Möglichkeiten des Einsatzes einer dynamischen Geometriesoftware in dieser Unterrichtsreihe a) Wiederholung der Grundkonstruktionen: - Mittelpunkt einer Strecke - Mittelsenkrechte - Lot von einem Punkt auf eine Strecke - Parallele zu einer Geraden durch einen Punkt - Winkelhalbierende Führen Sie diese Konstruktionen doch einmal selbst durch. c) Winkel an Geradenkreuzungen Aufgabe: - Zeichnen Sie zwei Geraden, die sich auf dem Bildschirm nicht schneiden. - Bestimmen Sie an zwei verschiedenen Stellen den Abstand. - Zeichnen Sie eine dritte Gerade, die diese beiden Geraden schneidet. - Messen Sie z.B. zwei (zukünftige) Stufenwinkel. - Verschieben Sie die beiden ersten Geraden so lang, bis beide markierten Winkel gleich groß sind. - Vergleichen Sie den Abstand zwischen beiden Geraden. - (Das Verfahren kann natürlich auch für die anderen Winkelarten fortgesetzt werden) (Lösung in der Datei loesung1.geo) Auch sehr anschaulich ist die Lösung: winkel.geo [4] d) Winkelsumme im Dreieck - Der Beweis des Innenwinkelsatzes mit Hilfe der abgetrennten Winkel und und dem Zusammenlegen eines gestreckten Winkels am Winkel ist auch mit einer DGS nicht zu übertreffen. Gönnen Sie an dieser Stelle ihren Schülern mal ein wenig Luft. - Die Herleitung des Beweises kann natürlich auch mit Dynageo Euklid sehr gut - nachgestellt werden. - Eine schöne Lösung finden Sie auf [4]. 6/12 - weitere Anwendung: aus LS 7.Schuljahr S.93, Nummer 12 Die Vorlage und die Lösung finden Sie unter: angler-vorlage.geo und angler-lösung.geo e) Mittelsenkrechte und Umkreis Erste Möglichkeit: - Bearbeiten Sie das Arbeitsblatt auf www.fjls.de – Fächer – Mathematik Material 8. Schuljahr – Umkreis eines Dreiecks Zweite Möglichkeit: - Ein sehr genaues uns strukturiertes Arbeitsblatt finden Sie auf [2] (7. Klasse) f) Winkelhalbierende und Inkreis Hier kann nur empfohlen werden, die Konstruktion nach Einführung einmal mit Dynageo – Euklid durchzuführen. Ihre Schüler/innen werden sehr schnell merken, dass man den Inkreis nicht einfach ins Dreieck „fummeln“ kann. Die Konstruktion des Lotes als Radius des Kreises ist dringend erforderlich! Führen Sie diese Konstruktion durch. g) Satz des Thales Erste Möglichkeit: - Bearbeiten Sie das Arbeitsblatt auf www.fjls.de – Fächer – Mathematik – Material – 8. Schuljahr – Satz des Thales Zweite Möglichkeit: - Bearbeiten Sie die Datei thales.geo. 7/12 Zusatzaufgabe 1: Satz des Pythagoras Zeichnen Sie die „Pythagorasfigur“. Achten Sie darauf, dass das Dreieck rechtwinklig und veränderbar ist. Zusatzaufgabe 4: Vielleicht sind Sie ja auch Physiklehrer. Die Linsengleichung lässt sich in Kombination mit einer Tabellenkalkulation mit diesem Arbeitsblatt schnell finden Zusatzaufgabe 2: 8/12 Zusatzaufgabe 3: Euklid eignet sich auch als Funktionsplotter: 1 Schalten Sie in der Leiste Koordinatensystem 2 das ein. Wechseln Sie zu und legen Sie sich auf der x-Achse einen Punkt fest, indem Sie erst auf klicken und dann auf die x-Achse. Benennen Sie den Punkt durch Doppelklick auf den Punkt mit A. Dieser Punkt sollte sich jetzt auf der x-Achse frei verschieben lassen. 3 Es soll der Graph der Funktion y = x2 erzeugt werden. Klicke Sie auf und tragen folgende Werte ein: Bestätigen Sie mit OK. Benennen Sie den Punkt B. Wenn Sie jetzt A bewegen, sollte sich B auf einer Parabel bewegen. 4 Gehen Sie wieder zur und dort auf . Klicken Sie auf den Punkt B und bewegen Sie A entlang der gesamten x-Achse. Sie erhalten eine (eventuelle etwas krumme) Parabel. 5 Klicken Sie mit der rechten Maustaste auf die Parabel und dann auf STANDARDKURVE. Jetzt sollte die Parabel „schön“ aussehen. 6 Es ist auch möglich über Schieberegler einzelne Parameter zu variieren. Es soll die Funktion y = a · x2 dargestellt werden. 7 Gehen Sie auf und fügen Sie ein Zahlobjekt ein. Klicken Sie mit der rechten Maustaste auf das Zahlobjekt und benennen Sie es a. 8 Klicken Sie mit der rechten Maustaste auf den Punkt B und gehen Sie zu KOORDINATEN EDITIEREN. Geben Sie folgende Werte ein: 9 . Bestätigen Sie mit OK. Fertig. Wenn Sie am Zahlobjekt schieben oder ziehen, verändert sich der Graph. 9/12 10/12 3. Interessante Links zu Euklid Dynageo [1] www.dynageo.de Die Seite des Entwicklers des Programms. Hier gibt es die neueste Programmversion. Trägt man sich in die Liste ein, wird man benachrichtigt, wenn es Programmaktualisierungen gibt. In einem Forum wird einem bei Fragen schnell und kompetent geholfen. [2] www.dynama.de Unterrichtsmaterialien für die Realschule Eine riesige Sammlung von Arbeitsblättern und Dynageo-Dateien. Alle Daten sind nach Klassenstufen sortiert und lassen sich schnell finden. Zum Teil stehen komplette Unterrichtseinheiten zur Verfügung. [3] http://hischer.de/uds/lehr/vum/dgs/ Die Spezialität dieser Seite sind Online-Kurse zu diesem Programm. In sehr detaillierten Übungen könne Sie Ihr Wissen komplettieren. Einzelne Übungen sind auch zur direkten Arbeit mit den Schülern gedacht. [4] http://www.briegelonline.de/mathe/euklid.htm Das ist die Partnerseite von [2] mit einigen Angeboten speziell für die Realschule. [5] http://www.pa.asnsbg.ac.at/pasbg2/mathematik/cabrihelp/index.htm Eine Online-Anleitung und unzählige fertige Arbeitsblätter zu Cabri II. 11/12 4. Ausblick a) Programme Dynageo-Euklid ist nur eines von einigen am Markt befindlichen dynamischen Geometriesoftwaren (DGS). Für das Land Hessen existiert eine Landeslizenz, die jeder Lehrer und Schüler auf seinem heimischen Computer verwenden darf. Eine Liste weiterer Programme finden Sie auf [2]. Dynamische Geometriesoftware am V200 von Texas Instruments: Über zahlreiche Menüs lässt sich Cabri analog zu Euklid bedienen. Hier ein Beispiel einer Spiegelung am V200: b) Motivation der Schüler Betrachten Sie DGS und „händisches“ Konstruieren nie als entweder-oder. Nutzen Sie DGS ganz gezielt, um forschend-entdeckendes Lernen bei Ihren Schülern zu fördern. Sie werden sehen – die Motivation ist enorm. Falls alle Schüler der Klasse über einen Computer, eventuell sogar mit Internetanschluss, verfügen (was in der Realschule wohl noch selten der Fall ist), können Sie DGS auch gut zur Bearbeitung von Hausaufgaben einsetzen. Aus eigener Erfahrung kann ich Ihnen sagen, dass Hausaufgaben vor Ihnen zu Hause sind. Lassen Sie Ihre Schüler auch mal ein wenig spielen. c) Einsatz in anderen Klassenstufen Der Einsatz von DGS ist in allen Klassenstufen möglich und nicht nur in der Geometrie. Dynageo-Euklid eignet sich auch hervorragend als Funktionsplotter, also auch zum Einsatz in der Analysis. d) Effektive Unterrichtsgestaltung Verbringen Sie nicht zu viel Zeit damit, im Internet nach Arbeitsblättern für Ihr Thema zu suchen. Schauen Sie sich ein paar Ideen ab und entwerfen Sie selbst ein Arbeitsblatt zugeschnitten auf Ihre Lerngruppe. Viele Beweisaufgaben aus dem Lehrbuch eigenen sich zur unmittelbaren Verwendung von DGS! Zeitplan: 12/12