Station 1: Normalparabeln

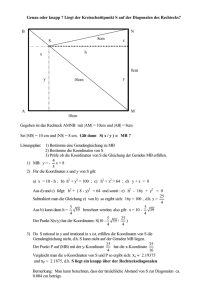
Ähnlichkeit – Sachaufgaben Strahlensätze
1. Diese Blume ist 8cm groß, und sie steht ¼m vor der Lampe.
Wie weit hinter die Blume muss man die Leinwand stellen,
damit der
Schatten
genau 14cm
groß ist?
2. Im Dreieck ABC sind die Seiten a und b jeweils 150cm lang. Die vom Punkt C
ausgehende Höhe hat eine Länge von 60 cm. Man will ein anderes
gleichschenkliges Dreieck konstruieren, in dem der Winkel γ genau so groß
wie im Dreieck ABC ist, die Höhe hc aber 80cm lang ist. Wie lang sind dann
die beiden gleich langen Seiten?
3. Im abgebildeten Kegel ist h = 35cm und s = 42cm.
Diesem Körper soll die Spitze abgeschnitten werden,
so dass ein Kegelstumpf entsteht, welcher nur noch
20cm hoch ist. Wie könnte man die Schnittlinie
anzeichnen? Verwende den ersten Strahlensatz!
4. Ein 1,35m hoher Stab wirft einen 2m langen Schatten. Wie hoch ist ein
Baum, der zur gleichen Zeit einen 32m langen Schatten wirft?
5. Im Trapez ABCD ( AB || CD ) schneiden sich die Diagonalen im Punkt P.
Man stellt fest, dass die Länge der Diagonale AC 8cm und die Länge der
Diagonalen BD 10cm beträgt. Wie lang ist die Strecke AP , wenn man zudem
weiß, dass der Diagonalenschnittpunkt P genau 4cm vom Punkt D entfernt
ist?
Lösungen
25cm 25cm  x

8cm
14cm
25cm
25 + x = 43,75 | -25
x
8cm
x = 18,75cm
Die Leinwand muss 18,75cm hinter die Blume gestellt werden.
150cm
x
150cm  80cm

x


= 200cm
60cm 80cm
60cm
Die Schenkel dieses Dreiecks sind dann genau 2m lang.
35cm 35cm  20cm
42cm  15cm

 s' 
= 18cm
42cm
s'
35cm
Man könnte eine 18cm lange Schnur an der
Kegelspitze befestigen und auf der Mantelfläche
markeiren, wo diese Schnur endet.
1,35m
x
1,35m  32m

x


= 21,6m
2m
32m
2m
Der Baum ist 21,60m hoch.
AC PC

BD PD
8cm
PC

also
 PC = 3,2cm
10cm 4cm
 AP  AC  PC = 8cm - 3,2cm = 4,8cm
14cm