Klausur Geoinformation I – Fragen zur Vorbereitung

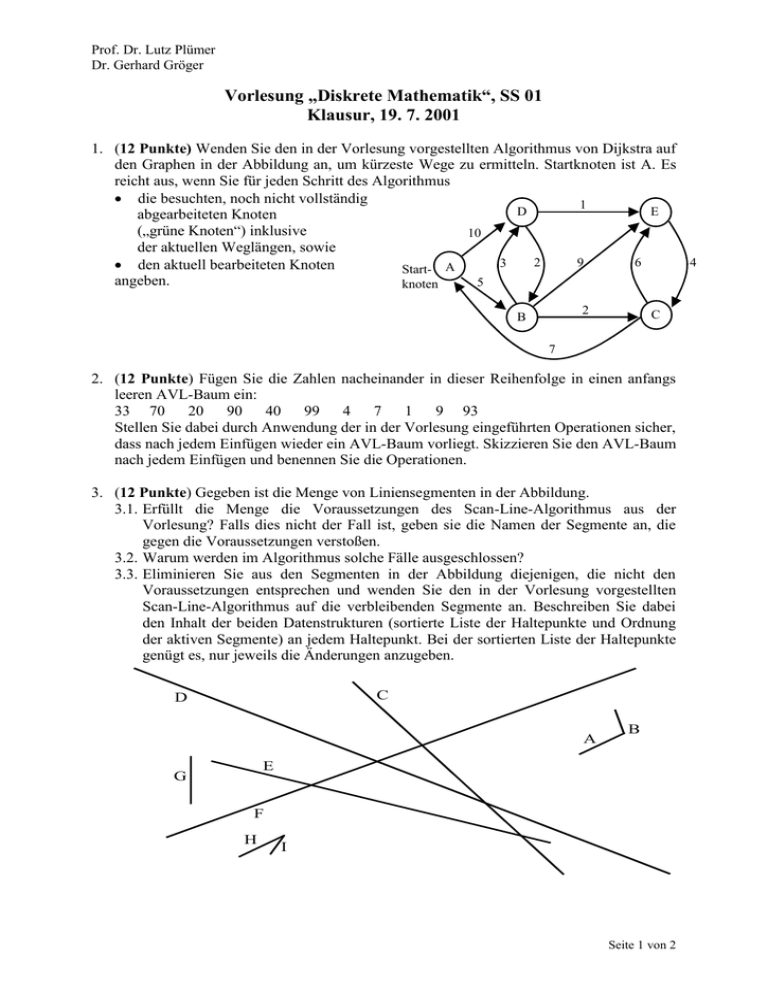
Prof. Dr. Lutz Plümer
Dr. Gerhard Gröger
Vorlesung „Diskrete Mathematik“, SS 01
Klausur, 19. 7. 2001
1. (12 Punkte) Wenden Sie den in der Vorlesung vorgestellten Algorithmus von Dijkstra auf
den Graphen in der Abbildung an, um kürzeste Wege zu ermitteln. Startknoten ist A. Es
reicht aus, wenn Sie für jeden Schritt des Algorithmus
 die besuchten, noch nicht vollständig
1
D
E
abgearbeiteten Knoten
(„grüne Knoten“) inklusive
10
der aktuellen Weglängen, sowie
2
9
6
4
3
 den aktuell bearbeiteten Knoten
Start- A
angeben.
5
knoten
2
B
C
7
2. (12 Punkte) Fügen Sie die Zahlen nacheinander in dieser Reihenfolge in einen anfangs
leeren AVL-Baum ein:
33 70
20
90
40
99
4
7
1
9 93
Stellen Sie dabei durch Anwendung der in der Vorlesung eingeführten Operationen sicher,
dass nach jedem Einfügen wieder ein AVL-Baum vorliegt. Skizzieren Sie den AVL-Baum
nach jedem Einfügen und benennen Sie die Operationen.
3. (12 Punkte) Gegeben ist die Menge von Liniensegmenten in der Abbildung.
3.1. Erfüllt die Menge die Voraussetzungen des Scan-Line-Algorithmus aus der
Vorlesung? Falls dies nicht der Fall ist, geben sie die Namen der Segmente an, die
gegen die Voraussetzungen verstoßen.
3.2. Warum werden im Algorithmus solche Fälle ausgeschlossen?
3.3. Eliminieren Sie aus den Segmenten in der Abbildung diejenigen, die nicht den
Voraussetzungen entsprechen und wenden Sie den in der Vorlesung vorgestellten
Scan-Line-Algorithmus auf die verbleibenden Segmente an. Beschreiben Sie dabei
den Inhalt der beiden Datenstrukturen (sortierte Liste der Haltepunkte und Ordnung
der aktiven Segmente) an jedem Haltepunkt. Bei der sortierten Liste der Haltepunkte
genügt es, nur jeweils die Änderungen anzugeben.
C
D
A
B
E
G
F
H
I
Seite 1 von 2
4. (12 Punkte) Der erste Schnittpunkt, der von dem Scan-Line-Verfahren gefunden wird, ist
nicht immer der am weitesten links liegende. Geben Sie ein Beispiel mit einer möglichst
kleinen Anzahl von Schnittpunkten an, bei dem der erste gefundene nicht der am
weitesten links liegende Schnittpunkt ist.
5. (12 Punkte) Gegeben sei das Voronoi-Diagramm einer Punktmenge P. Geben Sie einen
Algorithmus in Pseudo-Code an, der die konvexe Hülle von P aus dem VoronoiDiagramm ermittelt.
6. (16 Punkte) In der Abbildung ist eine Karte des Autobahnnetzes um Bonn gezeigt. Leiten
Sie aus dieser Darstellung einen Graphen her, der als Eingabe für den Algorithmus von
Dijkstra geeignet ist und der die Erreichbarkeit mit dem PKW repräsentiert. Beschränken
Sie sich dabei auf das Autobahnnetz (A555 und A565, das Autobahnkreuz AK Bonn
Nord, die Anschlussstellen AS Tannenbusch, AS Endenich, AS Poppelsdorf und AS
Lengsdorf) und die folgenden Zubringerstraßen: Hohe Straße, Verteilerkreis Bonn,
Herrmann Wandersleb-Ring, Endenicher Straße, Reuterstraße und Provinzialstraße. Die
Benennung der Knoten kann sich an der Beschriftung in der Karte orientieren.
Kantengewichte brauchen nicht berücksichtigt zu werden. Falls die Ab- und
Zufahrtmöglichkeiten in der Karte nicht denen in der Realität entsprechen, gehen Sie von
denen in der Karte aus.
St. Augustin
Köln
AS
Tannenbusch
AS
Lengsdorf
7. (12 Punkte) Gegeben sei eine einfach verkettete Liste von Elementen, die Integer-Werte
repräsentieren. Schreiben Sie ein Programm in Pseudo-Code, das überprüft, ob in der
Liste Elemente doppelt vorkommen (d.h. ob es mindestens zwei Elemente mit demselben
Integer-Wert gibt).
8. (12 Punkte) Schreiben Sie ein Programm in Pseudo-Code, das die Elemente eines binären
Suchbaums in absteigender Reihenfolge ausgibt.
Gesamtpunktzahl: 100
Seite 2 von 2
Viel Erfolg!
Seite 2 von 2