Harmonische Teilung

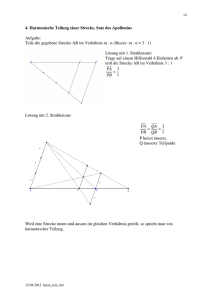
Harmonische Teilung, Inversion, Apollonios-Kreis
Diese Ausarbeitung stellt einen Gang durch die Geometrie der Verhältnisse dar, der die oben
genannten Begriffe und geometrischen Bereiche schlüssig miteinander in Verbindung bringt.
Wir gehen aus von einfachen Streckenteilungen, schließen harmonische Teilungen an, führen so zum
Begriff der Inversion, betrachten deren Invarianten - die Orthogonal-Kreise; Orthogonal-Kreise
wiederum erzeugen harmonische Teilungen.
An unterrichtlichen Voraussetzungen benötigen wir die Strahlensätze, den konstruierenden Umgang
mit ihnen, den Satz des Thales, den Satz des Pythagoras, den Kathetensatz und den konstruierenden
Umgang mit ihm, und sonst nur ein wenig elementare Geometrie.
1 Streckenteilung
1.1 Begriff der Teilung, Schreibweisen
Gegeben seien zwei Punkte A und B. Sie begrenzen eine Strecke AB. Ein weiterer Punkt C liege auf
AB. Wir sagen, C teilt B. Das Teilungsverhältnis geben wir durch den Bruch AC/BC an, der Teilpunkt
wird stets zuletzt genannt.
1.2 Satz von der Winkelhalbierenden
Um den Begriff der inneren Teilung zu motivieren, sehen wir uns den folgenden Satz an.
Satz: Die Winkelhalbierende eines Dreiecks
teilt die gegenüberliegende Seite im
Verhältnis der anliegenden Seiten.
Wie beweist man diesen Satz? Die
Verhältnisgleichung erinnert an den
Strahlensatz. Hier fehlen allerdings die
C
Parallelen. Aber AD und BD liegen
aneinander wie die von den Parallelen
abgeschnittenen Strahlenabschnitte. Und eine
Parallele zeichnet man leicht hinzu. Eine
g2
Parallele zu BC läßt zwar AC und BC als
g1
sinnvolle Teilstrecken erscheinen, aber so
kommt man nicht weiter. Eine Parallele g2
zur Winkelhalbierenden g1 durch B hindurch
ist vielversprechend. Wenn sie auf der
A
D
B
Verlängerung von AC über C hinaus die Seite
CE=BC erzeugte, wären wir fertig.
Das Dreieck BEC ist tatsächlich gleichschenklig, da  DCA = CBE (Wechselwinkel) und  DCA
= BEC (Stufenwinkel). Nun können wir den Strahlensatz anwenden und sehen AD/BD = AC/EC =
AC/BC.
1.3 Konstruktion einfacher
Teilung mit
Strahlensatz
B
Das Teilverhältnis AC/BC soll auf
eine Strecke AY übertragen
werden.
Zeichne in beliebigem Winkel AY
an AB, zeichne Gerade g1 durch B
und Y, konstruiere Gerade g2
durch C und parallel zu g1. g2
C
g1
g2
A
Z
Y
E
schneidet AY im gesuchten Teilpunkt Z.
1.4 innere und äußere Teilung
Mit C finden wir zu einer Strecke AB einen Teilpunkt. Kann man umgekehrt zu einem Punkt A bei
gegebenem Teilpunkt C den Endpunkt der Strecke B bestimmen? Zur Konstruktion hilft uns die
äußere Parallele.
Um den Begriff der Teilung zu erweitern, wollen wir auch einen Punkt D, der auf der Verlängerung
von AB über B hinaus liegt, als Teilpunkt auffassen. Im Falle des Punktes C sprechen wir von innerer
Teilung, im Falle des Punktes D von äußerer Teilung.
Bei der inneren Teilung bestimmt C zwei Summanden, sodass AC+BC = AB ist.
Bei der äußeren Teilung bestimmt D Minuend und Subtrahend, sodass AD–BD = AB ist.
1.5 Harmonische Teilung
Gibt es zu einem Teilpunkt C der Strecke AB einen äußeren Teilpunkt D mit gleichem Teilverhältnis?
Das probieren wir aus.
AC=2, BC=1, also AC/BC=2/1. Es müßte AD = 6 sein, dann ist BD = 3 und das Verhältnis ist gleich.
AC=5, BC=1, also AC/BC=5/1. Liegt jetzt D weiter rechts? Nein, denn dann würde das Verhältnis
AD/BD immer kleiner, genauer gesagt ginge es gegen 1. Nun müßte AD = 7,5 und BD = 1,5 sein und
das Verhältnis ist gleich.
Stimmen das innere und das äußere Teilverhältnis überein, so sprechen wir von harmonischer Teilung.
Es gilt dann also AC/BC=AD/BD.
Definition: Die Strecke AB wird durch die Punkte C und D harmonisch geteilt, wenn C auf AB und B
auf CD liegt und es gilt AC/BC=AD/BD.
1.6 Konstruktion harmonischer Teilung mit Strahlensatz
Zu gegebenem Teilverhältnis AC/BC ist der vierte Punkt D gesucht, der die Teilung harmonisch
macht. Da D außerhalb von AB liegt, spiegeln wir B´ über C.
B´
C
g2
B´´
g1
A
B
D
Zeichne in beliebigem Winkel AB´ an AB, zeichne Gerade g1 durch B´´ und B, konstruiere Gerade g2
durch C und parallel zu g1. g2 schneidet AB außen im gesuchten Teilpunkt D.
1.7 Konstruktion harmonischer Teilung mit Außenwinkelhalbierenden
Im Satz von der Winkelhalbierenden haben wir gesehen, dass ein Teilverhältnis der Seiten durch die
Winkelhalbierende auf eine Seite übertragen wird. Kann man diese Eigenschaft benutzen, um den
außen liegenden harmonischen Punkt zu finden?
E
g1
A
C
g2
B
D
Wir halbieren versuchsweise den Außenwinkel. Eine weitere Hilfsparallele und dieselbe
Argumentation wie im Beweis des Satzes von der Winkelhalbierenden führt zum Ziel. Wir können
den Satz von der Winkelhalbierenden allgemeiner formulieren:
Satz: Die Winkelhalbierende eines Dreiecks teilt die gegenüberliegende Seite innen im Verhältnis der
anliegenden Seiten, die Außenwinkelhalbierende teilt die gegenüberliegende Seite außen im Verhältnis
der anliegenden Seiten.
1.8 Grenzüberlegung als Hinführung zur Inversion (Kreis-Spiegelung)
Bei gegebener Strecke AB ist jedem inneren Teilpunkt C ein äußerer Teilpunkt D zugeordnet und
umgekehrt.
Wir beobachten die Lage von D abhängig von C. Liegt C nahe bei B, dann liegt auch D nahe bei B. Je
weiter C von B wegrückt, desto schneller bewegt sich D von B weg. Liegt C auf der Mitte von AB,
dann ist D unendlich weit von B entfernt. Die Abhängigkeit von C und D hat gewisse Ähnlichkeit mit
einer Spiegelung.
2 Inversion
2.1 Erklärung des Begriffs
Gegeben ist ein Kreis, den wir im allgeneinen als Einheitskreis auffassen können. Er hat den
Durchmesse AB und den Mittelpunkt M. C und D seien harmonische Teilpunkte von AB. Dann gilt
mit AC/BC = AD/BD und AM = MB = r:
(r + MC)/(r – MC) = ( r + MD)/(MD – r)
(r + MC)(MD – r) = ( r + MD)(r – MC)
rMD + MC MD – r2 – rMC
= r2 – rMC + rMD – MC MD
r2 = MC MD
r/MC = MD/r
1/ (MC/r) = MD/r
k1
D
C
M
A
MD ist also bis auf Streckung mit r der Kehrwert von MC
und umgekehrt. Diese Gleichung definiert die Spiegelung am
Kreis, die wir auch Inversion nennen.
B
Definition: Unter Inversion an einem Kreis mit Mittelpunkt M und Radius r verstehen wir eine
Abbildung, die einem Punkt C den Punkt D zuordnet dergestalt, dass 1/ (MC/r) = MD/r gilt.
Wir stellen fest:
Der Durchmesser eines Kreises wird von zwei am Kreis gespiegelten Punkten harmonisch geteilt.
2.2 Konstruktion des Bildpunktes unter
Inversion
B1
2.2.1 mit Strahlensatz
C1
B2
Den zu C bezüglich k1 inversen Punkt D finden wir mit
Hilfe der Strahlensatz-Konstruktion des harmonischen
Punktes.
D
B
M
C
A
k1
2.2.2 mit Kathetensatz
Da r2 = MC MD gilt, können wir mit b = r den Kathetensatz
anwenden. Dabei ist MD die Hypotenuse eines rechtwinkligen
Dreiecks, MC ist der zur Kathete b = r gehörende Abschnitt.
Ist umgekehrt der äußere Punkt D gegeben, und C gesucht,
konstruiert man den Kreispunkt P2 mit Thales-Kreis und fällt
das Lot auf MD.
h2
g3
g2
M
2.3 Orthogonal-Kreise
Dieser letzte Gedanke läßt uns ein zweites Thales-Dreieck in
der Zeichnung entdecken. CDP2 besitzt einen Umkreis, der
offensichtlich den Inversionskreis orthogonal schneidet. Sehen
wir uns diesen Kreis k2 genauer an. Er ist bestimmt durch die
Lage von C, D und dem Punkt P des Inversionskreises.
Jetzt bekommt die Gleichung r2 = MC MD plötzlich eine
weitere Bedeutung.
r2 ist das Quadrat eines Abschnittes der Tangente durch M
an den Kreis k2, MC und MD sind Abschnitte einer Sekante.
Nun gilt die Gleichung r2 = MC MD aber auch für jeden
anderen Kreis durch C und D, da er ja immer den
Inversionskreis schneidet. Der Radius r berührt aber
gleichzeitig den Kreis k2. Die Kreise verlaufen also
orthogonal zueinander. Es gilt somit der
Satz: Teilen die Punkte C und D die Strecke AB harmonisch,
so ist jeder Kreis durch C und D Orthogonal-Kreis zum Kreis
mit Durchmesser AB.
Und umgekehrt gilt:
Satz: Ist D das Bild von C bezüglich der Spiegelung an k,
dann ist jeder Kreis durch C und D Orthogonal-Kreis zum
Kreis k.
Und weiter:
Satz: Ist k2 ein Orthogonal-Kreis zu k1, dann existiert zu
jedem P aus k2 ein Q aus k2, welches das Bild von P unter
Inversion an k1 ist. Das heißt, der Orthogonal-Kreis k2 wird
in sich abgebildet.
D
B
C
k1
h2
g3
P
k2
k1
g2
D
B
C
M
A
P
k2
k1
r
D
B
M
A
C
2.4 Invarianten
Eben haben wir festgestellt, dasss Orthogonal-Kreise in sich abgebildet werden. Solche Kreise nennen
wir Fixkreise; sie sind unter der Abbildung invariant. Gibt es noch weitere Invarianten? Der
Inversionskreis selbst ist bezüglich der Inversion invariant. Er besteht aus Fixpunkten, die jeweils auf
sich selbst abgebildet werden. Auch Ursprungsgeraden sind invariant, da alle ihre Punkte wieder auf
die Gerade selbst abgebildet werden. Ursprungsgeraden sind Fixgeraden.
2.5 Bilder von Geraden und Kreisen
Wie werden beliebige Geraden und beliebige Kreise abgebildet? Besitzen sie besonders geartete
Bilder, wie es die Ursprungsgeraden und die Orthogonalkreise zeigten?
3 Apollonios-Kreis
Erinnern wir uns noch einmal an die harmonischen Punkte. Oben haben wir zu gegebenem
Teilverhältnis passende Punkte auf AB konstruiert. Ein Punkt X, der die Gleichung AC/BC=AX/BX
erfüllt, muss aber nicht unbedingt auf AB liegen. Im Falle der harmonischen Teilung haben wir ihn
außerhalb von AB gefunden. Im Satz von der Winkelhalbierenden war X die dritte Ecke des Dreiecks.
Der griechische Mathematiker Apollonios fand heraus, dass alle diese Punkte X auf einem Kreis
liegen. Wir wollen seinen Gedankengang nachvollziehen.
Ist X ein Punkt außerhalb von AB mit AX/BX=const., dann liegt ein Punkt C der Strecke AB mit
AC/BC=const. auf der Winkelhalbierenden von Winkel AXB. Der dazu passende harmonische Punkt
D auf AB liegt auf der Außenwinkelhalbierenden. Diese beiden Winkelhalbierenden schneiden sich in
X orthogonal. Das Dreieck CDX ist rechtwinklig, egal wo X liegt. Nach Thales bilden die Punkte X
also einen Kreis mit Durchmesser CD.
4 Koaxiale Kreise
eventuell weglassen?
5 Hilfssätze
5.1 Sekanten-Tangenten-Satz
6 Literatur
6.1 C. Stanley Ogilvy: Unterhaltsame Geometrie, Vieweg Braunschweig 1984
6.2 Coxeter/Greitzer: Zeitlose Geometrie, Klett Stuttgart 1983
6.3 Roger A. Johnson, Advanced Euclidean Geometry, Dover Publications New
York 1960
Autor:
StD Michael Spielmann
Wolfgangstr. 14
42655 Solingen