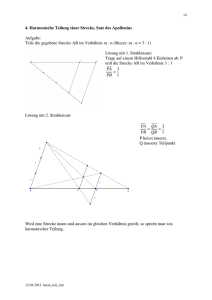
Die harmonische Teilung

Harmonische Teilung
Ein wenig Harmonik
Das Gebiet der ästhetischen Qualitäten mathematischer Proportionen hat schon seit
Jahrhunderten Anlass zu zahllosen Kontroversen gegeben. Nach von Naredi-Rainer1 gehört die
Frage nach der richtigen Proportion zu den faszinierendsten und zugleich umstrittensten
Problemen künstlerischen Gestaltens. Der goldene Schnitt ist wohl die bekannteste und vielleicht
auch beliebteste Proportion, aber er ist keineswegs alleiniger Repräsentant von Schönheit.
Albrecht Dürer, welcher sich ein Leben lang mit Proportionen beschäftigt hat, erkannte
schliesslich, dass es ein einziges „rechtes Mass“ als das „wirklich Beste“ und absolut Schöne
nicht geben kann. Die Natur offenbare sich in vielfältigen Formen und erlaube daher nur die
Erkenntnis einer „bedingten Schönheit“2.
Rationale oder kommensurable3 Proportionen spielen in der Architektur der Antike, des
Mittelalters und der frühen Neuzeit eine hervorragende Rolle. Kommensurable Proportionen
erscheinen auch in der musikalischen Harmonielehre, bei den pythagoreischen und reinen
Intervallen. Nach eingehenden Untersuchungen der Proportionen an den Tempeln von Paestum
kommt Hans Kayser, der in unserer Zeit die „Harmonik“ (die Theorie der kommensurablen
Proportionen) neu aufgegriffen hat, zur Auffassung, Architektur sei „gefrorene“ Musik4.
Mittelbildung
Wir beginnen mit dem Vergleich des arithmetischen, des geometrischen und des harmonischen
Mittels von zwei positiven reellen Zahlen p, q. Das arithmetische Mittel ist gegeben durch
pq
. Das geometrische Mittel wird definiert durch mg  p  q . Schliesslich versteht
ma 
2
2 pq
man unter dem harmonischen Mittel den Ausdruck mh 
. Man beachte, dass
pq
2 pq
1

pq
1 1 1
  
2 p q
Somit ist das harmonische Mittel von p und q gleich dem Kehrwert des arithmetischen Mittels
der Kehrwerte von p und q.
Ferner erkennt man leicht, dass mh  ma  mg 2 und somit mh : mg  mg : ma . Auf dieser
Proportion beruht eine sehr ansprechende Visualisierung der drei Mittel im rechtwinkligen
Dreieck mit den Hypotenusenabschnitten p und q (s. Figur)5. Wir nehmen hier an, dass p  q ist.
1
2
3
4
5
Paul von Naredi-Rainer: Architektur und Harmonie. Zahl, Maß und Proportion in der abendländischen
Baukunst. Dumont, Köln 1982
Erwin Panofsky: Das Leben und die Kunst Albrecht Dürers. München 1977
Streckenlängen heissen kommensurabel, falls sie ein gemeinsames Mass besitzen; d.h., falls es eine Strecke e
gibt derart, dass die gegebenen Streckenlängen ganzzahlige Vielfache der Länge von e sind.
Hans Kayser: Lehrbuch der Harmonik, Occident-Verlag, Zürich, 1950
Auf diese Figur wurden wir von Heinz Surber (St. Gallen) aufmerksam gemacht.
Seite 1
Vergleich der drei Mittel von p  AH und q  BH
Dabei ist M der Mittelpunkt der Hypotenuse und H der Höhenfusspunkt. Die Ecke C liegt ja auf
dem Thaleskreis über AB; deshalb ist MC das arithmetische Mittel von p und q. Dass HC
deren geometrisches Mittel ist, folgt aus dem Höhensatz. Da sich J C zu HC gleich verhält
wie HC zu MC , folgt aus obiger Bemerkung, dass J C das harmonische Mittel von p
und q ist. 
Aus Figur 1 liest man übrigens die Ungleichung
mh  mg  ma
ab. Dabei gilt Gleichheit offensichtlich nur dann, wenn p  q ist.
Die harmonische Teilung
Strecken können nicht nur innen sondern auch aussen in einem gegebenen Verhältnis geteilt
werden. Die Figur zeigt die Konstruktion der inneren und äusseren Teilung einer gegebenen
Strecke AB im Verhältnis 3:2. Werden die Teilungspunkte mit X (innen) bzw. Y. (aussen)
bezeichnet, so gilt somit AX : BX  AY : BY  3 : 2 .
Innere und äussere Teilung der Strecke AB im Verhältnis 3:2.
Man zeigt nun leicht, dass die Länge der Strecke AB das harmonische Mittel der Streckenlängen
AX und AY ist:
Zum Beweis setzen wir
Seite 2
x : AX , b : AB , y : AY .
Nach Voraussetzung gilt
x : (b  x )  y : ( y  b)
oder, anders geschrieben
x ( y  b)  (b  x)  y

Löst man diese Gleichung nach b auf, so ergibt sich
b 
2x y
,
x y
also ist AB das harmonische Mittel von AX und AY , wie behauptet wurde. •
Aus diesem Grund spricht man in der gegebenen Situation auch von harmonischer Teilung: In
Figur 2 teilen die Punkte X und Y die Strecke AB harmonisch im Verhältnis 3:2. Man beachte,
dass hier die Strecke AB als gerichtete Strecke zu betrachten ist. Die Strecke BA wird durch die
Punkte X, Y harmonisch im Verhältnis 2:3 geteilt.
Die harmonische Teilung ist im Grunde eine Eigenschaft von vier Punkten auf derselben
Geraden. Genauer gilt nämlich:
Teilen die Punkte X und Y die Strecke AB harmonisch, so teilen auch die Punkte
B und A die Strecke YX harmonisch.
Denn aus AX : BX  AY : BY folgt sofort auch XB : YB  XA : YA . Folglich gilt
auch: Die Streckenlänge Y X ist das harmonische Mittel von YB und Y A .
Der Harmonische Wurf

•



Die folgende äusserst elegante Konstruktion der harmonischen Streckenteilung nennt man
„harmonischen Wurf“; er beruht auf einem Ergebnis der Projektiven Geometrie.
Die Strecke AB werde durch den Punkt X innen im Verhältnis m : n geteilt. Wir wollen zu den
drei Punkten A, B und X den vierten harmonischen Punkt konstruieren, dh. denjenigen Punkt Y,
der die Strecke AB aussen im Verhältnis m : n teilt. Die Gerade durch A und B nennen wir im
Folgenden die Basis. Wir ziehen durch A zwei beliebige Geraden g, h und durch B eine weitere
Gerade k, welche sich aber nicht in einem einzigen Punkt treffen (vgl. die Figur).
Seite 3
Konstruktion des Punktes Y so, dass X und Y die Strecke AB harmonisch teilen.
Die Geraden g und k schneiden sich im Punkt N; h und k im Punkt Q. Nun verbinden wir X mit N
durch die Gerade l; h und l schneiden sich im Punkt P. Die Verbindungsgerade von B und P
schneidet g in O (vgl. Figur 3). Schliesslich legen wir die Gerade durch O und Q, welche die
Basis im vierten harmonischen Punkt Y schneidet. Diese Konstruktion beruht darauf, dass das
Viereck NOPQ als perspektivisches Bild eines Parallelogramms mit der Basis als Fluchtgerade
interpretiert werden kann6.
Der Kreis des Apollonios
Man kann eine Strecke aber auch im gegebenen Verhältnis m : n innen und aussen teilen, indem
man wie folgt vorgeht:
Über der Strecke AB konstruieren wir ein Dreieck ABC mit den Seitenlängen AC  me und
BC  ne (wobei die positive reelle Zahl e so zu wählen ist, dass m e  n e  AB ; vgl. Figur
4). Durch B wird nun eine Paralelle zu AC gelegt und von B aus auf beiden Seiten Strecken der
Länge ne abgetragen. Die Endpunkte D‘ bzw. D“ verbinden wir mit C, und die
Verbindungsgeraden, die wir mit w‘ bzw. w“ bezeichnen,schneiden wir mit der Gerade durch A
und B. Die Schnittpunkte werden mit X bzw. Y bezeichnet. Nach dem zweiten Strahlensatz
haben wir die Strecke AB somit innen und aussen im gleichen Verhältnis m : n geteilt.
Die Punkte X, Y teilen die Strecke AB harmonisch im Verhältnis m : n .
6
Für eine ausführlichere Darlegung werden tiefer liegende Begriffe aus der projektiven Geometrie benötigt (s.
z.B. [Ha])

Seite 4
Weil nun sowohl die Winkel BDX und ACX (Wechselwinkel an Parallelen) als auch
BDX und BCX (Basiswinkel des gleichschenkligen Dreiecks CDB ) gleich sind, gilt auch
ACX  BC X . Analog kann man zeigen, dass die Gerade w“ die Halbierende des
zugehörigen Aussenwinkels ist. Daraus folgt der
Satz von den Winkelhalbierenden im Dreieck
Die Halbierenden eines Dreieckswinkels und des zugehörigen Aussenwinkels teilen
die Gegenseite harmonisch im Verhältnis der anliegenden Seiten.
Da sich Innen- und Aussenwinkel bei C zu einem gestreckten Winkel ergänzen, bilden die
Winkelhalbierenden w‘ und w“ einen rechten Winkel. Errichten wir nun den Kreis mit
Durchmesser XY, so muss dieser durch C gehen (Thaleskreis). Nimmt man umgekehrt irgend
einen Punkt C‘ auf diesem Kreis an, so gilt stets AC  : BC   m : n , d.h. dass bei
Verschiebung der Ecke C längs des Kreises über XY das Verhältnis der Seitenlängen unverändert
bleibt.
Kreis des Apollonios zur Strecke AB und zum Verhältnis AX : BX
Dieser Kreis ist somit der geometrische Ort aller Punkte, deren Abstände von den Endpunkten
einer Strecke ein konstantes Verhältnis haben. Die beidenPunkte, welche die gegebene Strecke
in diesem Verhältnis harmonisch teilen, bestimmen den Durchmesser des Kreises (vgl. Figur 5).
Ausserdem gehen die Halbierenden des Winkels AC’B und seines Aussenwinkels stets durch X
bzw. Y
Diesen Kreis nennt man den zur Strecke AB und dem Verhältnis m : n gehörigen ApolloniosKreis; er ist benannt nach Apollonios von Perge7. Der Apollonios-Kreis wird auch
Divisionskreis (Ort gleicher Quotienten von zwei Punkten aus) genannt.
7
Apollonios von Perge (262-190 v. Chr.), griechischer Mathematiker und Astronom, verfasste ein achtbändiges
Werk über Kegelschnitte
Seite 5