Uebung2_Loesg

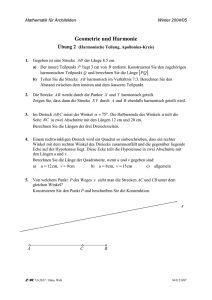
Mathematik für Architekten
Winter 2004/05
Geometrie und Harmonie
Lösungen zur Uebung 2
1.
Wir verwenden die Bezeichnungen b  AB , p  AP , q  AQ . Falls P und Q die
Strecke harmonisch in einem bestimmten Verhältnis teilen, so gilt
AP : BP  AQ : BQ
und mit den eingeführten Bezeichnungen
p : (b  p)  q : (q  b) (*)
a)
Konstruktion mittels paralleler Hilfsgeraden durch A und B.
Berechnung: Es gilt b  8.5 cm und p  5.5 cm . Man löst die Gleichung (*) nach q
auf und bestimmt dann PQ  q  p .
Aus (*) folgt zunächst die Produktform
p (q  b)  (b  p) q .
Mit etwas Umformen ergibt sich daraus
2 pq  bq  bp .
q
Weiteres Umformen liefert
PQ  q  p 
bp
. Schliesslich erhalten wir
2b  p
2 p (b  p)
bp
p 
 13.2 cm
2p  b
2p  b
p : (b  p)  q : (q  b)  7 : 3 .
b) In diesem Fall gilt
Somit erhalten wir
3p  7(b  p)
3q  7(q  b) .
zunächst die Produktformen
und
10 p  7b
4q  7b .
Daraus kann man p und q bestimmen:
und
7
Also gelten p  10
b und q  74 b und somit
PQ  q  p 
2.
7
4
b  107 b 
21
20
b  8.925 cm .
Wenn die Strecke AB durch die Punkte X und Y harmonisch geteilt wird, so gilt
AX : BX  AY : BY .
Dann gilt aber auch
AX : AY  BX : BY ,
anders geschrieben
XA : YA  XB : YB ,
d.h. A und B teilen die Strecke XY harmonisch.
Z :W, 14.5.2016 / Hma, Web
–1–
75904028
Mathematik für Architekten
3.
Winter 2004/05
Nach Voraussetzung gelten u  20 cm, v  12 cm,   75 .
Nach dem Satz von der Winkelhalbierenden gilt
ferner
AC : BC  u : v .
Es gibt also einen Proportionalitätsfaktor k so,
dass
AC  k  u ,
BC  k  v .
A
Der Cosinussatz liefert nun
C
/2 /2
u
B
v
(u  v)2  (k  u)2  (k  v)2  2(k  u)(k  v)cos75
Diese Gleichung muss nun nach k aufgelöst werden. Zunächst ergibt sich
k 2  u2  v 2  2uvcos75  (u  v)2
Schliesslich erhalten wir k 
uv
u 2  v 2  2uv cos75
 1.56187
Daraus folgt:
AC  k  u  31.24cm , BC  k  v  18.74cm und natürlich AB  32cm .
4.
Wir behandeln den allgemeinen Fall
(Aufgabenteil c)):
Das Dreieck ABC habe bei C einen rechten
Winkel. Wir setzen a  BC und
b  AC . Die Diagonale des Quadrates ist
die Halbierende des rechten Winkels. Nach
dem Satz von der Winkelhalbierenden gilt A
somit
C
x
x
u
v
B
b:a  u:v .
Daraus folgt b 
a u
, und der Satz von Pythagoras liefert
v

 u2  v 2 
 au 
u2 
(u  v)  a  b  a     a 2  1  2   a 2 
.
 v 

 v 2 
v 
(u  v)v
Aufgelöst nach a erhalten wir a 
. Nach dem 2. Strahlensatz haben wir ferner
u2  v 2
ua
uv
x 

x : u  a : (u  v) .
Zusammen ergibt sich
uv
u2  v 2
2
2
Daraus erhält man
Z :W, 14.5.2016 / Hma, Web
2
2
a)
2
x 
12  9
122  92
 7.2cm
–2–
b)
x 
8 15
82  152
 7.06 cm
75904028
Mathematik für Architekten
Winter 2004/05
5.
Beschreibung der Konstruktion:
1. Bestimme den Punkt D der die Strecke AB aussen im selben Verhältnis teilt wie C.
2. Konstruiere den Kreis mit dem Durchmesser CD.
Dieser Kreis ist der geometrische Ort aller Punkte P mit der Eigenschaft, dass die
Halbierende des Winkels R APB durch den Punkt C geht. Also ist dieser Kreis auch
der geometrische Ort aller Punkte, von denen aus die Strecken AC und CB unter dem
gleichen Winkel gesehen werden.
3. Schneide den Kreis mit der Geraden s. Die beiden Schnittpunkte sind die gesuchten
Lösungen.
6.
Es sei F der Punkt des Planes, der dem Flughafen entspricht. Nach Voraussetzung gilt:
AF : BF : CF  1: 12 : 13  6 : 3: 2 .
Beschreibung der Konstruktion:
1. Teile die Strecke AB harmonisch im Verhältnis 2 :1 und konstruiere den
zugehörigen Apolloniuskreis. Dieser Kreis ist der geometrische Ort aller Punkte,
welche von A doppelt so weit entfernt sind wie von B. Also muss der gesuchte Punkt
F auf diesem Kreis liegen.
2. Teile die Strecke AC harmonisch im Verhältnis 3 :1 und konstruiere den
zugehörigen Apolloniuskreis.
3. Die beiden Kreise schneiden sich in zwei Punkten. Beide erfüllen die Bedingung, die
an F gestellt wurde. Man wird den Punkt bevorzugen, der im Inneren des Dreiecks
ABC liegt.
7.
a) Man wähle eine Strecke der Länge b  c  10cm und zeichne den Kreis mit dieser
Strecke als Durchmesser.
Nun passe man in diesen Kreis eine Sehne ein, welche die Länge 2a  8cm hat und
auf dem gegebenen Durchmesser senkrecht steht.
Der Schnittpunkt S von Durchmesser und Sehne teilt den Durchmesser in zwei
Abschnitte. Nach dem Sehnensatz ist das Produkt ihrer Längen gleich a 2 . Also sind
die beiden Abschnitte die gesuchten Rechtecksseiten b und c.
b) Man zeichne einen Kreis mit einem Durchmesser der Länge b  c  6 cm.
Dann trage man auf einer beliebigen Tangente an diesen Kreis vom Berührungspunkt
A eine Strecke der Länge a  4cm ab; der Endpunkt werde mit P bezeichnet.
Nun zeichne man die Gerade ein, die durch P und den Kreismittelpunkt geht; sie
schneide den Kreis in den Punkten B und C, wobei C zwischen P und B liegt.
Setze b  PB und c  PC .
Nach dem Tangentensatz gilt jetzt b  c  a 2 ; d.h. die Strecken PB und PC sind die
gesuchten Rechtecksseiten.
Z :W, 14.5.2016 / Hma, Web
–3–
75904028
Mathematik für Architekten
8.
Winter 2004/05
Der erste Lösungsschritt ist rein
gedanklicher Natur. Der
geometrische Ort aller Punkte,
von denen aus das Bild unter
demselben Winkel gesehen wird
ist der Fasskreis für diesen
Winkel. Zu vorgegebenem Winkel
konstruiert man diesen Kreis,
indem man benützt, dass der
zugehörige Zentriwinkel doppelt
so gross ist. In der Figur ist ein
solcher Fasskreis samt halbem
Zentriwinkel eingezeichnet.
4,40 cm
3,00 cm
Wird nun der Radius des
Fasskreises vergrössert, so wird der zugehörige Winkel kleiner; wird der Radius hingegen
verkleinert, so nimmt der Winkel zu. Es geht also darum, einen möglichst kleinen Kreis
zu finden, der aber die Augenhöhe des Beobachters gerade noch trifft. Dies ist offenbar
der Fasskreis, welcher die Linie der Augenhöhe berührt.
a)
Nach dem Tangentensatz gilt jetzt a  (a  h)  x 2 und somit x  a (a  h) .
D.h. die gesuchte Streckenlänge ist das geometrische Mittel von a und a  h .
b) Nun zur Konstruktion: Es
geht also darum, das
geometrische Mittel aus
zwei vorgegebenen
Streckenlängen zu finden.
Dazu gibt es verschiedene
Konstruktionsmethoden. In
der nebenstehenden Figur
ist der Euklidsche
Kathetensatz angewendet
worden.
4,40 cm
3,00 cm
x
Z :W, 14.5.2016 / Hma, Web
–4–
75904028