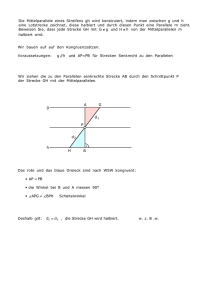
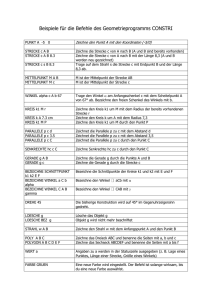
(Länge und Breite des Fußballplatzes) mit GeoGebra

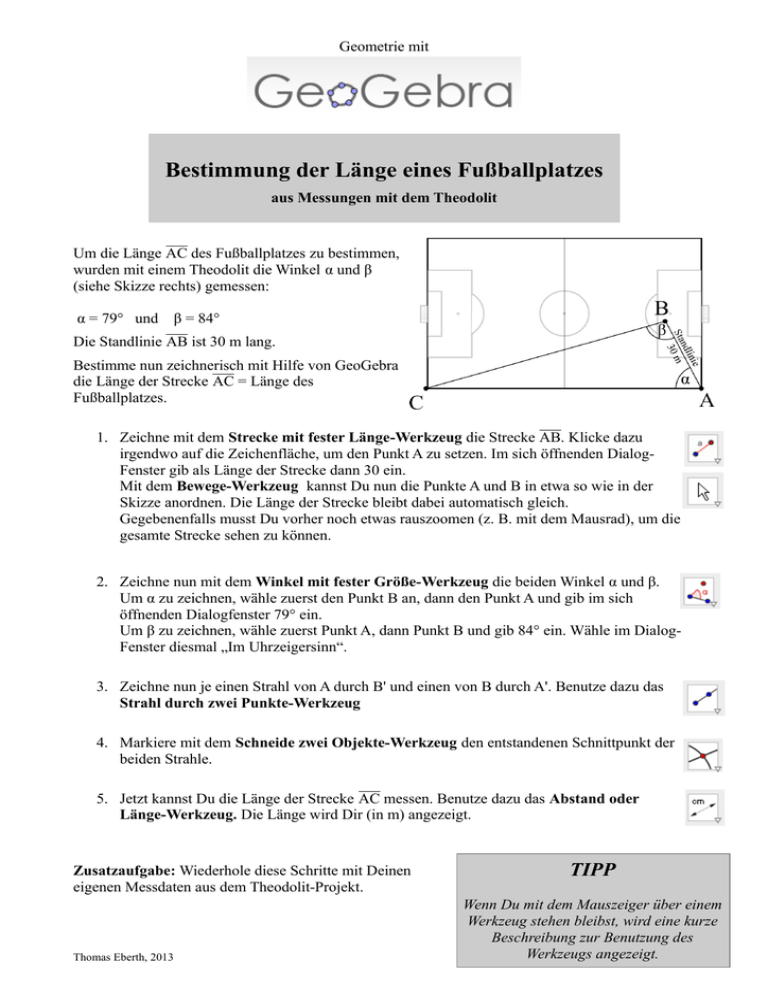
Geometrie mit
Bestimmung der Länge eines Fußballplatzes
aus Messungen mit dem Theodolit
Um die Länge AC des Fußballplatzes zu bestimmen,
wurden mit einem Theodolit die Winkel α und β
(siehe Skizze rechts) gemessen:
α = 79° und
β = 84°
Die Standlinie AB ist 30 m lang.
Bestimme nun zeichnerisch mit Hilfe von GeoGebra
die Länge der Strecke AC = Länge des
Fußballplatzes.
1. Zeichne mit dem Strecke mit fester Länge-Werkzeug die Strecke AB. Klicke dazu
irgendwo auf die Zeichenfläche, um den Punkt A zu setzen. Im sich öffnenden DialogFenster gib als Länge der Strecke dann 30 ein.
Mit dem Bewege-Werkzeug kannst Du nun die Punkte A und B in etwa so wie in der
Skizze anordnen. Die Länge der Strecke bleibt dabei automatisch gleich.
Gegebenenfalls musst Du vorher noch etwas rauszoomen (z. B. mit dem Mausrad), um die
gesamte Strecke sehen zu können.
2. Zeichne nun mit dem Winkel mit fester Größe-Werkzeug die beiden Winkel α und β.
Um α zu zeichnen, wähle zuerst den Punkt B an, dann den Punkt A und gib im sich
öffnenden Dialogfenster 79° ein.
Um β zu zeichnen, wähle zuerst Punkt A, dann Punkt B und gib 84° ein. Wähle im DialogFenster diesmal „Im Uhrzeigersinn“.
3. Zeichne nun je einen Strahl von A durch B' und einen von B durch A'. Benutze dazu das
Strahl durch zwei Punkte-Werkzeug
4. Markiere mit dem Schneide zwei Objekte-Werkzeug den entstandenen Schnittpunkt der
beiden Strahle.
5. Jetzt kannst Du die Länge der Strecke AC messen. Benutze dazu das Abstand oder
Länge-Werkzeug. Die Länge wird Dir (in m) angezeigt.
Zusatzaufgabe: Wiederhole diese Schritte mit Deinen
eigenen Messdaten aus dem Theodolit-Projekt.
Thomas Eberth, 2013
TIPP
Wenn Du mit dem Mauszeiger über einem
Werkzeug stehen bleibst, wird eine kurze
Beschreibung zur Benutzung des
Werkzeugs angezeigt.