Erläuterungen zu den Lösungen der Aufgaben zur Trigonometrie

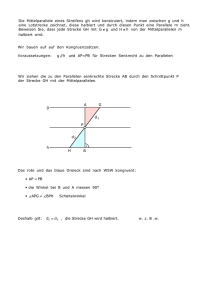
Erläuterungen zu den Lösungen der Aufgaben zur Trigonometrie
Link: Lösungen der Aufgaben
Aufgabe 1
Das Dreieck CFB ist ein rechtwinkliges Dreieck.
Die Strecke FB steht senkrecht auf der Strecke CF, sie ist damit die Höhe im Dreieck CFB.
Die Strecke C ist die Hypothenuse im Dreieck CFB.
Für den Winkel  gilt daher: sin  
Gegenkathe te Strecke CB a  b


Hypothenuse
Strecke C
c
Für den Winkel  gilt weiter : cos 
Ankathete
Strecke FB b


Hypothenuse Strecke C c
Aus der Gleichung
sin 2   cos 2   1

a b b
2
2
2

     1  a  2ab  2b  c
 c  c
2
2
Damit ist gezeigt:
Länge der Strecke CF2  Länge der Strecke FB2  Länge der Strecke C2
Die Geometrie der Aufgabenstellung beweist somit den Satz des Phytagoras für das Dreieck CFB.
Die Lösungen der Aufgabe zeigen, dass es nicht nur eine Lösung für das Problem gibt.