Geometrie und Harmonie

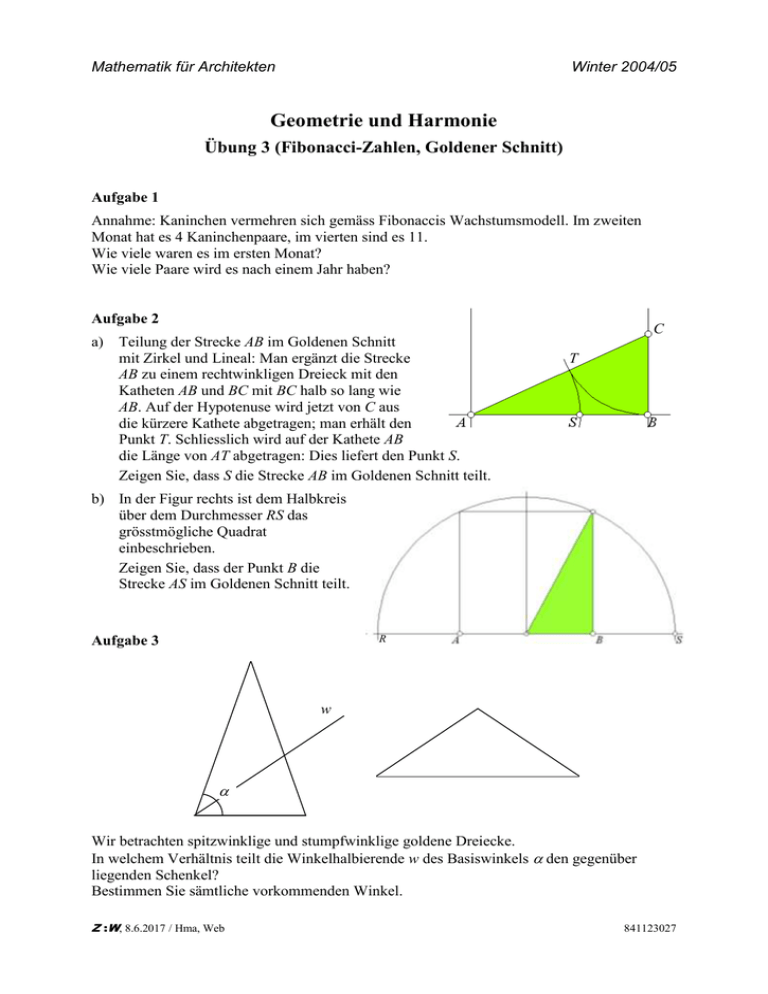
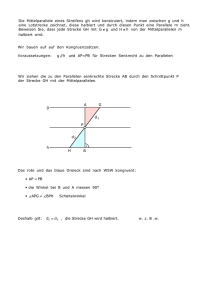
Mathematik für Architekten
Winter 2004/05
Geometrie und Harmonie
Übung 3 (Fibonacci-Zahlen, Goldener Schnitt)
Aufgabe 1
Annahme: Kaninchen vermehren sich gemäss Fibonaccis Wachstumsmodell. Im zweiten
Monat hat es 4 Kaninchenpaare, im vierten sind es 11.
Wie viele waren es im ersten Monat?
Wie viele Paare wird es nach einem Jahr haben?
Aufgabe 2
C
a) Teilung der Strecke AB im Goldenen Schnitt
mit Zirkel und Lineal: Man ergänzt die Strecke
AB zu einem rechtwinkligen Dreieck mit den
Katheten AB und BC mit BC halb so lang wie
AB. Auf der Hypotenuse wird jetzt von C aus
die kürzere Kathete abgetragen; man erhält den
Punkt T. Schliesslich wird auf der Kathete AB
die Länge von AT abgetragen: Dies liefert den Punkt S.
Zeigen Sie, dass S die Strecke AB im Goldenen Schnitt teilt.
T
b) In der Figur rechts ist dem Halbkreis
über dem Durchmesser RS das
grösstmögliche Quadrat
einbeschrieben.
Zeigen Sie, dass der Punkt B die
Strecke AS im Goldenen Schnitt teilt.
Aufgabe 3
R
w

Wir betrachten spitzwinklige und stumpfwinklige goldene Dreiecke.
In welchem Verhältnis teilt die Winkelhalbierende w des Basiswinkels  den gegenüber
liegenden Schenkel?
Bestimmen Sie sämtliche vorkommenden Winkel.
Z :W, 8.6.2017 / Hma, Web
841123027
Mathematik für Architekten
Winter 2004/05
Aufgabe 4
a)
Die folgenden Gleichungen sind Spezialfälle einer Formel von Simson1 über die
Fibonacci-Zahlen.
1 3  22  1 , 2  5  32  1 , 3 8  52  1, 5 13  82  1 , usw.
Wie lautet die allgemeine Formel?
b) Das nachstehende Paradox von Lewis Carroll2 ist eine amüsante Illustration der Formel
von Simson: Das Quadrat mit der Seitenlänge 13 wird gemäss Figur zerlegt und zu einem
Rechteck mit den Seitenlängen 8 und 21 wieder zusammengesetzt. Da stimmt doch etwas
nicht!?
A
C
B
B
A
D
D
C
Aufgabe 5
Konstruieren Sie reguläre n-Ecke mit Seitenlänge s für
a)
n  5, s  8cm
b)
n  10, s  6cm
c)
n  15, s  4cm
Aufgabe 6
Mit  wird der numerische Ausdruck für die Proportion des Goldenen Schnittes bezeichnet.
1 5
Es gilt also:  
.
2
Vereinfachen Sie die nachstehenden Terme so, dass  nur noch linear vorkommt:
a)
1
2
32  1
b)
4
c)
2 1
 1
Robert Simson (1687–1768), schottischer Mathematiker
Lewis Carroll (1832–1898), eigentlich Charles Lutwidge Dodgson, englischer Mathematiker und
Kinderbuchautor („Alice in Wonderland“)
Z :W, 8.6.2017 / Hma, Web
841123027