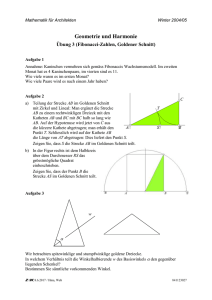
rein rechnerische Aufgaben

rein rechnerische Aufgaben
1. Gegeben ist ein gleichschenkliges Dreieck mit dem Winkel 36◦ bei der Spitze. Die
Winkelhalbierende eines Basiswinkels treffe den gegenüberliegenden Schenkel im
Punkt P . Zeige anhand einer übersichtlichen Skizze, daß der Punkt P den Schenkel
nach dem Goldenen Schnitt teilt!
(Hinweis: Verwende ähnliche Dreiecke!)
Lösung:
2. Der Unterschied der Längen der Abschnitte einer nach dem Goldenen Schnitt geteilten Strecke beträgt 5 cm. Wie lang ist diese Strecke und wie groß sind ihre Abschnitte?
√
Lösung: Strecke: 5 · ( 5 + 2) cm; Abschnitte:
5
2
√
· ( 5 + 3) cm,
5
2
√
· ( 5 + 1) cm
3. Dem Quadrat ABCD der Seitenlänge 1 wird wie in der Zeichnung ein Halbkreis
umbeschrieben. Zeige durch Rechnung: B teilt die Strecke [AE] im Verhältnis des
goldenen Schnitts.
...............
..........
...........
............
.....
D
C
.........
..............................................................................................................................
.........
..................................
.
.. ....
...... ....
... .. ...........
...
......
.....
... ...
.....
...
.....
.. ..
.....
....
...
.. ....
....
.
.
.
....
.
.
...
..
.
.
....
.
.
.
.
.
.
.
...
...
.
..
...
.
.
.
.
.
...
.
.
...
.
.
..
...
.
.
.
.
.
.
...
.
...
.
..
.
.
.
.
.
.
...
...
.
.
.
.
...
...
.
.
.
.
...
.
.
.
.
..
...
.
.
.
...
.
.
.
...
..
.
.
.
.
.
...
...
.
.
..
.
.
.
.
.
.
...
...
.
.
.
..
.
.
.
.
...
...
.
.
.
.
...
.
.
....
...
.
.
.
.
.
..
.
.
.
.
.
...
.
.
..
.
.
.
...
.
...
...
.
.
.
.
.
....
.
..
.
...
..
..
..
..
.
...
.
.
.
..
..
.
.
.
.
.
...
.
.
...
.
.
.
.
.
.......................................................................................................................................................................................................................................................
r
A
Lösung: Es ist r =
√
5
2
also
AB
AE
=
1√
1
+ 25
2
r
=
√
5−1
2
B
E
.
4. ABCDE ist ein regelmäßiges Fünfeck, d. h.
seine Seiten sind gleich lang, seine Innenwinkel gleich groß.
(a) Begründe:
i. <
) DAC =<
) QCD =<
) ACE
ii. Die Dreiecke ADC und AQC sind
gleichschenklig.
iii. Die Dreiecke ADC und CQD sind
ähnlich.
iv. AD : DC = CQ : QD
(b) Begründe, daß Q die Strecke AD im
goldenen Schnitt teilt.
1
A
..................................
................ ........................... ..........................
...........
.........
...... .. .. ......
.........
........
..... .... ..... ..........
.......
.
.......
.
.
.
.
.
.
.
.
.
......
.
..
......
...
..
......
......
......
......
...
..
.
.....
......
......
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
......
.....
.
...
...
.
.
.
.
.
.
.
.
.
.
.
.....
.
.
.
.
......
...
.
...
...
.
.
.
.
....
.
.
.
.
.
.
.
.
...
......
..
.
...
....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
......
...
...
.
...
....
.
.
.
.
.
.
...
.
.
.
.
.
......
...
.
..
....
...
.
.
.
.
.
.
.
.
.
.
.
......
...
...
.
..
....
.
.
.
.
.
.
.
.
.
.
.
......
...
...
.
....
.
.
...
.
.
...
.
.
.
.
.
.
......
...
.
.
....
...
.
.
.
.
.
.
.
.
.
.
.
......
...
.
..
.
... ..........
.
.
.
.
...... ....
...
...... ...
...
....
.... ..........
...... ..
.......
.
.
.
.
.
...
.
.
..........................................................................................................................................................................................................................................................................
...
..
.... .. ..
.. .. .......
...
...... .. ..
...
... .... ........
...... .... ....
...
.
.
.
.
.... .... ...........
.
....
.
...
......
......
... ....
..
...
.. .....
......
.....
...
...
...
..
......
......
...
...
..
..
...
...
......
......
...
...
..
.....
..
......
.
.
.
.
.
...
.
....
.
....
.
.
.
...
......
...
.
.
.
.
...
.
.
.
..
.
.
.
..
.
.
.
.
......
...
....
.
.
...
...
.
.
.
.
.
.
.
.
.
.
.
.
...... ..
... .....
..
...
.
...
.
.
.
.
.
.
.
.
.
.
.
.
.......
...
....
..
.
.
.
.
.
.
.
.
.
.
.
.
.
...
.
.
...
.
.
.... ....
.
.. ...........
.
.
.
.
.
...
...
.
.
.
...
......
.....
...
...
...
...
...
......
...
.....
...
...
......
...
...
...
......
...
......
...
...
..
..
..
......
...
......
...
..
.....
...
..
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...... .....
...
...
...
...
...
...
...
...
...
........
..
...
...
...... ...........
...
...
...
..
......
..
..
...
......
...
...
...
.....
......
..
..
.
.
...
.
...
.
.
.
.
.
.
.
.
.
.
.
.
......
...
...
...
..
......
......
...
...
...
...
...
...
......
......
...
...
...
...
...
.....
......
...
...
..
...
......
...
......
...
.
...
..
..
......
.
.
.
.
.
.
.
.
.
.
.... ..... ....
.
.
.
.
.
......
.... .. .. .........
...... .... ... ......
.... ... ... ......
...... ... ... .....
..... .. . ......
..... .. . .....
..............
...........................................................................................................................................................................
......
..
.......
......
.......
.......
.
.
.
.
........
.
.
.....
.
..........
.
.
.
.
.
.
.
...
.............
.............................................................
R
E
S
Q
B
T
P
D
C
Lösung: (a) (i) Umfangswinkelsatz für Sehnen gleicher Länge. (ii) Aus der Regularität des Fünfecks ergibt sich z. B., daß EAD ∼
= BCA, deswegen ist ADC gleichschenklig. AQC ist
wegen der Identität aus (i) gleichwinklig “. (iii) Übereinstimmung in drei Winkeln.
”
(iv) Folge der Ähnlichkeit.
(b) Ersetze in der Proportion DC und CQ durch AQ.
5. Im Dreieck ABC teilt der Punkt Q die Seite
[AB] im goldenen Schnitt. Ferner gilt AQ =
CQ = BC.
A.....
(a) Zeige, daß die Dreiecke ABC und CQB
ähnlich sind und berechne alle Innenwinkel des Dreiecks ABC.
(b) Beschreibe wie man, ausgehend von
diesem Dreieck, ein reguläres Fünfeck
konstruieren kann.
.....
... ....
... ..
.. ....
.
...
...
...
...
...
...
...
...
....
...
.
.
...
....
...
.
.
...
...
....
.
...
.
...
..
.
...
....
...
...
...
.
.
...
..
.
...
...
....
...
.
.
...
....
...
.
.
...
....
...
.
...
.
...
....
.
...
.
...
..
.
...
....
...
.
.
...
...
....
.
...
.
...
....
...
...
...
...........
...
. .....
.
...
......
...
......
....
.
......
...
.
......
...
..
.
......
...
......
....
...
......
.
.
...
......
......
....
...
......
.
...
.
......
...
....
......
...
.
......
.
...
......
..
.
......
...
..
.
.
.
......
...
..
......
...
.
......
...
....
......
...
......
...
...
......
.
.
......
...
..
.
.
......
.
..
.
.
.
...... .....
..
...... ..
.
.........
..
.
....................................................................................................................................................................................
Q
B
C
Lösung: (a) Weil Q die Strecke [AB] im goldenen Schnitt teilt und wegen der Gleichheiten AQ =
CQ = BC ergibt sich AB : BC = CQ : QB. Also sind ABC und CQB ähnlich.
Daraus ergibt sich <
) α = 360 und <
) β =<
) γ = 720 .
(b) Das Fünfeck erhält man z. B. durch Antragen der 720 -Winkel im Mittelpunkt eines
Kreises.
2