Beispiele für Produkte und Lösungen der

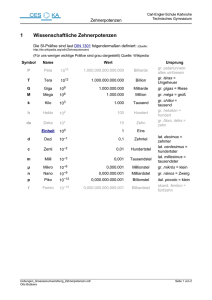
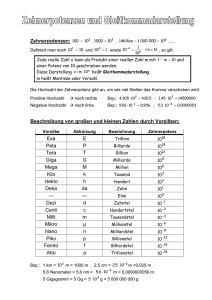
Zehnerpotenzen
1. Mit Hilfe von Zehnerpotenzen können wir ganz große Zahlen abkürzen. Dabei gibt die
Hochzahl an, wie oft der Faktor 10 in einer Zahl vorkommt. Übertrage die Tabelle in
dein Heft und fülle die Lücken aus.
Hundert
100
= 10 ∙ 10
102
Tausend
1 000
= 10 ∙ 10 ∙ 10
103
Zehntausend
10 000
= 10 ∙ 10 ∙ 10 ∙ 10
Hunderttausend
100 000
= 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10
Million
1 000 000
= 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10
Zehnmillionen
10 000 000
Hundert Millionen
100 000 000
Milliarden
1 000 000 000
Billionen
1 000 000 000 000
2. Berechne und schreibe das Ergebnis als Zahl und in Worten.
a. Verwende zunächst keinen Taschenrechner.
Hundert mal Hundert
Hundert mal Tausend
Hundert mal Zehntausend
Hundert mal Hunderttausend
Tausend mal Tausend
Tausend mal eine Million
Tausend mal eine Milliarde
b. Überprüfe die Ergebnisse von a mithilfe des Taschenrechners. Erkläre die Anzeige
des Taschenrechners.
3. Ein Mensch besitzt ca. 100.000 Haare auf dem Kopf. Legt man 10 Haare ganz dicht
nebeneinander, so sind diese etwa 1 mm breit.
a. Wie breit wäre ein Streifen, wenn du 100.000 Haare nebeneinander legst?
b. Wie breit wäre der Streifen, wenn du eine Billion Haare nebeneinander legst? Gib die
Breite auch als Zehnerpotenz an.
Seite 1 von 6
4. Schreibe folgende Zahlen als Zehnerpotenz und in Worten.
0,1; 0,01; 0,001;
1
1
1
;
;
10 100 1.000
1; 10; 100; 1.000; 1.000.000
5. Schreibe das Ergebnis als Zehnerpotenz
a. ohne Verwendung des Taschenrechners.
aa) 10∙10; 10∙1.000; 10∙10.000; 100∙105 ; 1.000∙1012
bb) 0,1∙0,1; 0,01∙0,01; 0,1∙0,01; 0,1∙10-3 ; 0,01∙10-7
cc) 10.000∙10-3 ; 100∙10-7 ; 0,01∙103 ; 0,001∙105
b. Überprüfe deine Ergebnisse mit dem Taschenrechner.
Seite 2 von 6
Beispiele für Produkte und Lösungen der Schülerinnen und Schüler
1. Mit Hilfe von Zehnerpotenzen können wir ganz große Zahlen abkürzen. Dabei gibt die
Hochzahl an, wie oft der Faktor 10 in einer Zahl vorkommt. Übertrage die Tabelle in
dein Heft und fülle die Lücken aus.
Hundert
100
= 10 ∙ 10
102
Tausend
1 000
= 10 ∙ 10 ∙ 10
103
Zehntausend
10 000
= 10 ∙ 10 ∙ 10 ∙ 10
104
Hunderttausend
100 000
= 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10
105
Million
1 000 000
= 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10
106
Zehnmillionen
10 000 000
= 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10
107
Hundert Millionen
100 000 000
= 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10
108
Milliarden
1 000 000 000
= 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10∙ 10∙ 10∙ 10
109
Billionen
1 000 000 000 000
=10∙10∙10∙10∙10∙10∙10∙10∙10∙10∙10
1010
2. Berechne und schreibe das Ergebnis als Zahl und in Worten.
a. Verwende zunächst keinen Taschenrechner.
Hundert mal Hundert:
10.000
Hundert mal Tausend
100.000
Hundert mal Zehntausend
1.000.000
Hundert mal Hunderttausend
10.000.000
Tausend mal Tausend
Tausend mal eine Million
Tausend mal eine Milliarde
1.000.000
1.000.000.000
1.000.000.000.000
Zehntausend
Hunderttausend
Million
Zehnmillionen
Million
Milliarde
Billion
b. Überprüfe die Ergebnisse von a mithilfe des Taschenrechners. Erkläre die Anzeige
des Taschenrechners.
Schülerantwort
Seite 3 von 6
3. Ein Mensch besitzt ca. 100.000 Haare auf dem Kopf. Legt man 10 Haare ganz dicht
nebeneinander, so sind diese etwa 1 mm breit.
a. Wie breit wäre ein Streifen, wenn du 100 000 Haare nebeneinander legst?
10 Haare ≜ 1 mm
100.000 Haare ≜ 1 ∙ 10.000 = 10.000 mm = 1.000 cm = 10 m
b. Wie breit wäre der Streifen, wenn du eine Billion Haare nebeneinander legst? Gib die
Breite auch als Zehnerpotenz an.
10 Haare ≜ 1 mm
1.000.000.000.000 ≜ 1 ∙ 100.000.000.000 = 100.000.000.000 mm
= 10.000.000.000 cm
= 100.000.000 m
= 100.000 km = 105 km
4. Schreibe folgende Zahlen als Zehnerpotenz und in Worten.
0,1; 0,01; 0,001;
1 1
1
;
;
10 100 1.000
0,1:
10–1
10 hoch minus 1
0,01:
10–2
10 hoch minus 2
0,001: 10–3
10 hoch minus 3
1
10
:
1
100
:
1
1.000
:
10–1
10 hoch minus 1
10–2
10 hoch minus 2
10–3
10 hoch minus 3
1; 10; 100; 1 000; 1 000 000
1:
100
10 hoch 0
10:
101
10 hoch 1
100:
102
10 hoch 2
1.000:
103
10 hoch 3
1.000.000:
106
10 hoch 6
Seite 4 von 6
5. Schreibe das Ergebnis als Zehnerpotenz
a. ohne Verwendung des Taschenrechners.
aa) 10 ∙ 10; 10 ∙ 1.000; 10 ∙ 10.000; 100 ∙ 105 ; 1.000 ∙ 1012
10∙10 :
102
𝟏0∙1.000:
104
10∙10.000:
105
100∙105 :
107
1.000∙1012 :
1015
bb) 0,1∙0,1; 0,01∙0,01; 0,1∙0,01; 0,1∙10–3 ; 0,01∙10–7
0,1∙0,1 :
10–2
0,01∙0,01:
10–4
0,1∙0,01:
10–3
0,1∙10-3 :
10–4
0,01∙10-7 :
10–9
cc) 10.000∙10–3 ; 100∙10–7 ; 0,01∙103 ; 0,001∙105
10.000∙10–3 :
101
100∙10–7 :
10–5
0,01∙103 :
101
0,001∙105 :
102
b. Überprüfe deine Ergebnisse mit dem Taschenrechner.
Seite 5 von 6
Anregung zum weiteren Lernen
Film „Hoch 10“:
http://www.youtube.com/watch?v=SnPUx5yUkQo
Dieser Kurzfilm aus dem Jahr 1979 zeigt in neun Minuten sehr anschaulich die Größenverhältnisse
unseres Universums. Es werden die Zehnerpotenzen von 1024 bis 10−16 dargestellt.
Titel: Kleine Zahlen (Mediabox)
Begründung:
Film ist in einzelne Schritte eingeteilt, lässt sich individuell ansteuern und in einzelnen Stunden
ansehen, so dass einzelne Sequenzen nochmals angeschaut werden können.
Inhalt: Klärung von negativen Hochzahlen bei Zehnerpotenzen: Stationen 1 bis 10;
ab dann Vergleich von Zehnerpotenzen (nicht nötig)
https://mediathek.mebis.bayern.de/index.php?doc=search/query&identifier=BY-00000089
http://mediabox.br-online.de/boxen/grips_m01_natuerliche_zahlen_02/index.html
Titel: Große Zahlen (Mediabox)
Begründung:
Film ist in einzelne Schritte eingeteilt, lässt sich individuell ansteuern und in einzelnen Stunden
ansehen, so dass einzelne Sequenzen nochmals angeschaut werden können.
Inhalt: Klärung von negativen Hochzahlen bei Zehnerpotenzen: Stationen 1 bis 10;
ab dann Vergleich von Zehnerpotenzen (nicht nötig)
https://mediathek.mebis.bayern.de/index.php?doc=search/query&identifier=BY-00000088
http://mediabox.br-online.de/boxen/grips_m01_natuerliche_zahlen_01/index.html
Seite 6 von 6