Weg – Geschwindigkeit – Beschleunigung

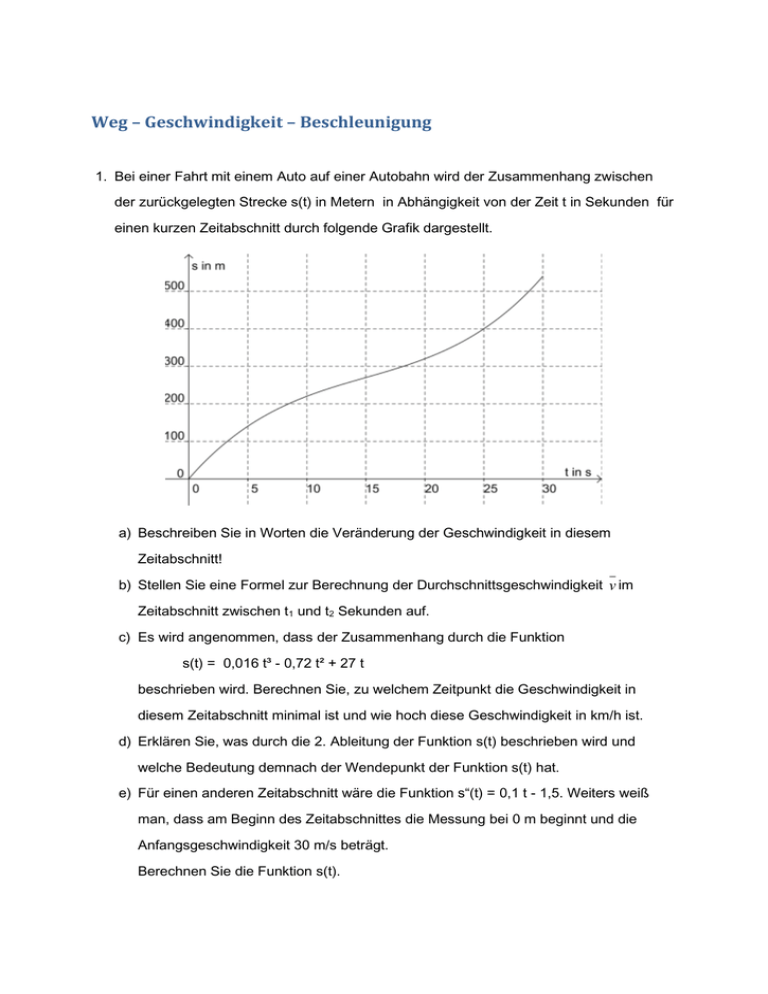
Weg – Geschwindigkeit – Beschleunigung
1. Bei einer Fahrt mit einem Auto auf einer Autobahn wird der Zusammenhang zwischen
der zurückgelegten Strecke s(t) in Metern in Abhängigkeit von der Zeit t in Sekunden für
einen kurzen Zeitabschnitt durch folgende Grafik dargestellt.
a) Beschreiben Sie in Worten die Veränderung der Geschwindigkeit in diesem
Zeitabschnitt!
b) Stellen Sie eine Formel zur Berechnung der Durchschnittsgeschwindigkeit v im
Zeitabschnitt zwischen t1 und t2 Sekunden auf.
c) Es wird angenommen, dass der Zusammenhang durch die Funktion
s(t) = 0,016 t³ - 0,72 t² + 27 t
beschrieben wird. Berechnen Sie, zu welchem Zeitpunkt die Geschwindigkeit in
diesem Zeitabschnitt minimal ist und wie hoch diese Geschwindigkeit in km/h ist.
d) Erklären Sie, was durch die 2. Ableitung der Funktion s(t) beschrieben wird und
welche Bedeutung demnach der Wendepunkt der Funktion s(t) hat.
e) Für einen anderen Zeitabschnitt wäre die Funktion s“(t) = 0,1 t - 1,5. Weiters weiß
man, dass am Beginn des Zeitabschnittes die Messung bei 0 m beginnt und die
Anfangsgeschwindigkeit 30 m/s beträgt.
Berechnen Sie die Funktion s(t).
2. Der Fahrtenschreiber eines LKW zeichnet die gefahrene Geschwindigkeit v(t) gemessen
in m/s in Abhängigkeit von der Fahrzeit t in Sekunden auf. Für einen kurzen
Zeitabschnitt wird dieser Zusammenhang durch folgende Grafik dargestellt.
a) Beschreiben Sie in Worten das Fahrverhalten des LKW!
b) Es wird angenommen, dass der Zusammenhang zwischen der zurückgelegten
Strecke s(t) in n und der Zeit t in Sekunden durch eine Funktion 3. Grades
beschrieben wird. Am Beginn der Aufzeichnung ist noch keine Strecke zurückgelegt
worden. Lesen Sie aus der Grafik die notwendigen Bedingungen zur Bestimmungen
dieser Funktion ab und berechnen Sie die Funktion s(t).
c) Erklären Sie, was mit der Formel
s(t2 )−s(t1 )
t2 −t1
bei einer Weg-Zeit Funktion s(t)
berechnet wird.
d) Für einen anderen Zeitabschnitt wird der Zusammenhang zwischen der
Geschwindigkeit v(t) in m/s und der Zeit t in Sekunden durch die Funktion v(t) = 0,009 t² + 0,5 t beschrieben. Berechnen Sie die Funktion s(t), die den
Zusammenhang zwischen der zurückgelegten Strecke s(t) in km und der Zeit t
beschreibt. Am Beginn der Aufzeichnung ist noch keine Strecke zurückgelegt
worden.
e) Die Änderung der Geschwindigkeit wird als Beschleunigung bezeichnet. Berechnen
Sie für die Funktion v(t) jene Funktion, die die Beschleunigung beschreibt und jenen
Zeitpunkt, bei dem die Beschleunigung den Wert 0 annimmt. Erklären Sie, welche
Bedeutung dieser Zeitpunkt für die Geschwindigkeit hat.
3. Ein Auto fährt auf der Bundesstraße. Seine Geschwindigkeit wird in einem kurzen
Zeitabschnitt durch folgende Grafik dargestellt:
a) Beschreiben Sie in Worten den Verlauf der Fahrt in diesem Zeitabschnitt.
b) Skizzieren Sie den Graphen der Zeit-Weg-Funktion.
c) In einem anderen Zeitabschnitt lautet die Gleichung der Zeit-Weg-Funktion:
t3
s(t) = − 120 +
t2
2
+ 10t
(s: Weg in Meter, t: Zeit in Sekunden, t ∈ [0, 20]).
Berechnen Sie
●
den Weg, den das Auto in diesen 20 Sekunden zurücklegt;
●
die Durchschnittsgeschwindigkeit in diesen 20 Sekunden;
●
die Momentangeschwindigkeit nach 10 Sekunden.
Ergebnisse:
1.
a) Die Geschwindigkeit nimmt bis zu einem bestimmten Wert ab (abbremsen) und
nimmt dann wieder zu.
b) v
̅=
s(t2 )−s(t1 )
t2 −t1
c) s(t) = 0,016 t³ -0,72 t² + 27 t
v(t) = s‘(t) = 0,048 t² - 1,44 t +27
v‘(t) = 0,096 t – 1,44 = 0 => t = 15
v(15) = 16,2 m/s = 58,32 km/h
d) s“(t) beschreibt die Änderung der Geschwindigkeit (Beschleunigung). Der
Wendepunkt der Funktion s(t) ist der Punkt bei dem die Beschleunigung 0 ist.
e) s“(t) = 0,012 t – 1,5
s‘(t) = 0,06 t² - 1,5 t + 30
s(t) = 0,02 t³ - 0,75 t² + 30 t
2.
a) Der LKW fährt aus dem Stillstand an, die Geschwindigkeit nimmt bis zu einem
maximalen Wert zu. Dann bremst der LKW ab, bis er zum Stillstand kommt.
b) s(0)=0, s‘(0)=0, s‘(60)=0, s‘(30)=9
s(t) = a t³ + b t ² + c t
s(t) = -0,003333 t³ + 0,3 t²
c) Mittlere Geschwindigkeit im Zeitraum zwischen t1 und t2 Sekunden
d) s‘(t)=-0,009 t² + 0,5 t
s(t) = 0,003 t³ + 0,25 t²
e) s“(t) = -0,018 t + 0,5
s“(t) = 0 => t = 27,77 s
Geschwindigkeit ist maximal
3.
a) Das Auto fährt zuerst mit 20 m(s. Es bremst 20 s lang bis auf 15 m/s ab und
beschleunigt dann wieder 20 s lang auf die ursprüngliche Geschwindigkeit.
b)
c) s(20) = 333,33m; v̅ =16,67 m/s = 60 km/h; v(10) = 17,5 m/s = 63 km/h