3. Ein Rennschlitten hat vom Start an die

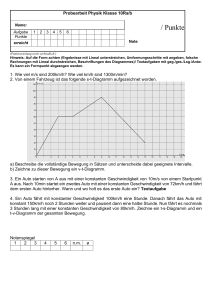
1. Klausur Physik Klasse 11
Grundkurs, 23.11.2010
Dauer: 45 min
1. Skizzieren Sie für die gleichförmige und die gleichmäßig beschleunigte Bewegung die s-t-, v-t
und a-t-Diagramme. (3)
2. Das Diagramm zeigt, wie die Geschwindigkeit eines Rennwagens während seiner zweiten
Runde auf einer drei Kilometer langen, flachen Rennstrecke variiert.
Die Abbildung darunter stellt den Streckenverlauf von fünf Rennstrecken dar. Auf welcher dieser
Rennstrecken fuhr der Wagen?
(Die Fahrt geht immer rechts herum)
3. Ein Rennschlitten hat vom Start an die gleichbleibende Beschleunigung von 2 ms -2.
a) Wie schnell fährt der Schlitten 5 Sekunden nach dem Start? (3)
b) Wie weit ist er gefahren, wenn seine Geschwindigkeit auf 20 ms -1 angewachsen ist? (3)
4. Ein Auto fährt aus dem Stillstand gleichmäßig an und erreicht nach fünf Sekunden eine
Geschwindigkeit von 50 kmh-1, mit der es auf die Autobahn fährt. Dort erreicht es nach
weiteren acht Sekunden eine Geschwindigkeit von 100 kmh -1. Bis zum nächsten
Bremsvorgang vergehen 7 Sekunden, in denen die Geschwindigkeit konstant bleibt.
a) Berechnen Sie für beide Beschleunigungsphasen die Beschleunigung. (3)
b) Welchen Weg hat das Auto insgesamt zurückgelegt? (6)
c) Zeichnen Sie für die gesamte Bewegung das v-t-Diagramm. (4)
Lösungen
1.
gleichförmige Bewegung
Weg-Zeit-Gesetz
gleichmäßig beschleunigte Bewegung
Weg-Zeit-Gesetz
Geschwindigkeit-Zeit-Gesetz
Geschwindigkeit-Zeit-Gesetz
Beschleunigung-Zeit-Gesetz
Beschleunigung-Zeit-Gesetz
2. B ist richtig. Der Wagen fährt als erstes durch eine flache Kurve, muss also nur leicht
Bremsen. Nach einer Geraden kommt eine sehr spitze Kurve, die Geschwindigkeit fällt
stark ab. Die folgende Gerade ist länger als die erste, der Wagen hat eine längere Strecke
eine konstante Geschwindigkeit. Nun kommt eine weitere Kurve, die wie die erste auch
relativ zügig durchfahren werden kann. Nach einer kurzen Geraden mit konstanter
Geschwindigkeit geht es dann wieder n die erste Kurve.
3.
geg.:
ges.: a) v
b) s
m
s2
t1 = 5 s
a= 2
m
s
a) Da die Bewegung aus dem Stand heraus erfolgt, kann man
schreiben:
v = a ⋅ t1
v 2 = 20
Lösung:
m
⋅ 5s
s2
m
v = 10
s
b) Da der Weg gesucht ist verwendet man
a
s = ⋅ t2
2
Die Zeit ist nicht bekannt, kann aber über die Geschwindigkeit
bestimmt werden:
v
a=
t
v
t=
a
Das wird eingesetzt:
a v2
s= ⋅ 2
2 a
v2
s=
2⋅ a
v= 2
2
Antwort:
m

 20 s 

s= 
m
2⋅ 2 2
s
s = 100m
a= Der Rennschlitten fährt nach 10 s 10 m/s. Wenn er 20 m/s
schnell ist, ist er 100 m weit gefahren.
4.
geg.:
ges.:
m
s
t1 = 5 s
v0 = 0
v1 = 50
a)a1,a2
b)s
km
h
t2 = 8 s
v 2 = 100
Lösung:
km
h
t3 = 7 s
a) Die Beschleunigung ist als die Geschwindigkeitsänderung je Zeit
definiert.
∆ v
∆t
km
km
50
−0
h
h
a1 =
5s
m
13,9
s
a1 =
5s
m
a1 = 2,8 2
s
km
km
− 50
h
h
a2 =
8s
km
50
h
a2 =
8s
m
13,9
s
a2 =
8s
m
a2 = 1,74 2
s
Der Gesamtweg setzt sich aus drei Teilwegen zusammen: erste
Beschleunigungsphase, zweite Beschleunigungsphase und gleichförmige
Bewegung.
s = s1 + s2 + s3
Der erste Weg berechnet sich mit
a
s1 = 1 t12
2
m
2,8 2
s ⋅ 52 s2
s1 =
2
s1 = 35m
Für den zweiten Weg muss beachtet werden, dass das Auto jetzt bereits
eine Geschwindigkeit hat.
a=
100
a2 2
⋅ t 2 + v1 ⋅ t 2
2
m
1,74 2
s ⋅ 8 2 s2 + 13,8 m ⋅ 8 s
s2 =
2
s
s2 = 55,7m + 110,4m
s2 =
s2 = 166,1m
Der dritte Weg berechnet sich mit
s3 = v 2 ⋅ t 3
m
⋅ 7s
s
s3 = 194,6m
Damit lässt sich der Gesamtweg berechnen:
s = s1 + s2 + s3
s3 = 27,8
s = 35m + 166,1m + 194,6m
s = 395,7m
c)