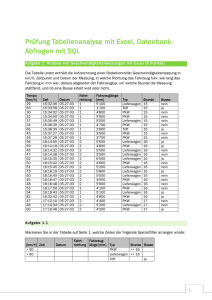
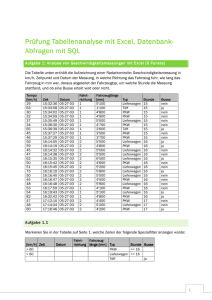
Übungsaufgabe 3 - jochen

Ein Fuhrunternehmer bezahlt monatlich 500 € Leasingraten für seinen Lieferwagen. Dieser
verbraucht auf 100 km 8 Liter Diesel (durchschnittlichen Dieselpreis pro Liter : 1,50€). Pro 1.000 km
muss 1 Liter Öl (Literpreis 20,- €) nachgefüllt werden. Außerdem fallen jährlich 400,- € für KFZ-Steuer
und 800,-€ für Versicherung an.
Es liegt dem Unternehmer ein Angebot für einen sparsameren Lieferwagen vor: Dieser braucht nur 6
Liter Diesel auf 100 km und der Motor ist dicht. Allerdings kommen zu den identischen Kosten für
Steuer und Versicherung noch höhere Leasingraten in Höhe von 700,- Euro.
Der Unternehmer berechnet seinen Kunden pro gefahrenem Kilometer 1,-€. Wegen schnellerer
Zustellung kann man mit dem neuen Lieferwagen einen höheren Preis (1,25€) pro km verlangen.
a) Ab welcher monatlichen Kilometerleistung lohnt es sich, auf den neuen Lieferwagen
umzusteigen?
b) Wie viele km muss der Fuhrunternehmer fahren, um mit den einzelnen Fahrzeugen Gewinn
zu erwirtschaften?
c) Wie viele km muss der Fuhrunternehmer fahren, um einen Monatsverdienst von 2.500,- € zu
haben?
d) Ab welcher km-Leistung ist der neue kostengünstiger?
e) Wie verändern sich die BEP, die kritische Menge und die kritische Gewinnmenge, wenn der
Benzinpreis auf 2,- € ansteigt?
Lösung:
1. Berechnung der kritischen Gewinnmenge:
G = m*db – Kf = U-K
U1 = p*m = 1m K= Kf + m*kv  Kf=
400+800
+
12
500 = 600,-
G1 = m -(600 + 0,14m) = 0,86m -600
G2 = 1,25m – (800+0,09m) = 1,16m -800
An der kritischen Gewinnmenge gilt : G1 = G2
 0,86m -600 = 1,16m -800
 200 = 0,3m  m= 666,66…
2. Berechnung der Gewinnschwelle:
G1 = m -(600 + 0,14m) = 0,86m -600 =! 0
𝟔𝟎𝟎
0,86m = 600  m = 𝟎,𝟖𝟔 = 697,67 km
1,5∗8
20
kv= 100𝑘𝑚 + 1000𝑘𝑚 = 0,14
G2 = 1,25m – (800+0,09m) = 1,16m -800 =!0
𝟖𝟎𝟎
1,16m = 800  m = 𝟏,𝟏𝟔 = 689,66 km
3. Gewinn von 2500 entsteht
 bei Lieferwagen 1, wenn
0,86m -600 =2.500
𝟑𝟏𝟎𝟎
m= 𝟎,𝟖𝟔 = 3.604,65 km
 bei Lieferwagen 2, wenn 1,16m -800 = 2.500  m= 2.844,83 km
4. Berechnung der kritischen Menge
K1 = K2
600 + 0,14m = 800+0,09m
0,14m-0,09m = 800-600
0,05m = 200
m = 4.000 km
5. Die erhöhten Spritpreise führen zu einer Erhöhung der variablen Stückkosten. Diese
müssen neu berechnet werden . Danach werden die Kosten- und Gewinnfunktionen neu
formuliert und die Berechnungen der Aufgaben 1-4 neu vorgenommen
Bsp. Lieferwagen 1:
2∗8
20
kv neu = 100km + 1000km = 0,18
Kf ist unverändert  K = 600 + 0,18m
 G = 1m – (600+0,18m)