Teil 1 - Antonkriegergasse

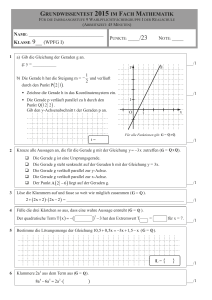
Jahresstoff der 5.Klasse im neuen Schularbeitsformat
Für jedes völlig richtig gelöste Beispiel gibt es einen Punkt. Sonst keinen Punkt.
1) Zahlenmengen
Kreuze die beiden zutreffenden Aussagen an!

Die Zahl

Die Zahl

Die Zahl

Die Zahl

Die Zahl
3
5 liegt nicht in
3
5 liegt in
, weil sie ein Bruch ist.
3
5 liegt in
, weil jede Zahl aus
3
5 liegt nicht in
3
5 liegt in

, weil sie negativ ist.

auch in

liegt.

, weil sie Dezimalstellen hat.

, weil Zähler und Nenner ganze Zahlen sind.
2) SI-Präfixe im Gleitkommaformat
Die Entfernung Wien-Berlin beträgt 5,3·102 km.
Aufgabenstellung:
Ordne die umgewandelten Zahlen den richtigen Einheiten zu!
5,3 · 105
A
mm
5,3 · 106
B
cm
7
C
m
5,3 · 108
D
dm
E
μm
F
nm
5,3 · 10
5,3 · 10
11
3) Prozentrechnung
Eine Ware kostet ohne Mehrwertsteuer 119 €. Es wird die Mehrwertsteuer von 20 % addiert. Im Ausverkauf ist die Ware dann
um 5 % verbilligt.
Aufgabenstellung:
Kreuze die zutreffende(n) Antwort(en) an!
119 1,2 bedeutet, dass zum Preis 20 % dazugerechnet wurden.
119 1,05 bedeutet, dass die Ware um 5 % verbilligt ist.


Wenn erst 20 % dazukommen und die Ware danach um 5 % billiger wird,
kostet sie 119 1,2 1,05 €

Die Reihenfolge der Berechnungen ist wichtig. Wenn man zuerst 20 %
addiert und dann 5 % subtrahiert erhält man ein anderes Ergebnis wie wenn
man zuerst 5 % subtrahiert und danach 20 % addiert.

Kreuze die zutreffende(n) Antwort(en) an!
Wenn eine Ware 3 mal um jeweils 5 % billiger wird, muss man den Preis mit
0,953 multiplizieren.

4) Ordne die Graphen den Funktionsgleichungen zu,
indem du f(x), g(x), h(x) und j(x) richtig zuordnest;
die 2 übrig gebliebenen Felder lässt du leer.
______ = -0.5x² + 4
______ = 0.5x² + 2
______ = x² - 2
______ = -x² - 2
______ = -x² - 4
______ = 0.5x² + 4
5) Gegeben ist der Graph einer quadratischen Funktion f.
a) Wie groß ist der Funktionswert an der Stelle 0?
b) Für welche x gilt f(x) = 4?
c) Gib f(2) an.
d) Wie lauten die Koordinaten des Scheitelpunktes?
6) Einheitskreis
Zeichne im Einheitskreis alle Winkel aus [0°; 360°] ein, für die gilt:
cos  = - 0,4 und überprüfe deine Zeichnung mit Hilfe des Taschenrechners!
1
b
0.5
1
0.5
0.5
0.5
1
1
7)
Die Zentripetalkraft beschreibt jene Kraft, die notwendig ist, um einen Körper der Masse m mit der
Geschwindigkeit v auf einer Kreisbahn mit dem Radius r zu halten!
Zentripetalkraft: F (m,r,v) =
m, v, r > 0
Ordne den Funktionen jeweils die passenden Funktionsgraphen zu:
F (m) =
r und v sind konstant
F (r) =
m und v sind konstant
F (v) =
m und r sind konstant
A
C
B
D
E
F
8) Von einem Graphen einer linearen Funktion f kennt man die folgenden beiden Punkte. Gib eine
Termdarstellung von f an! A(-1/-3), B(4/7)
9) Binomische Formeln
Welche der folgenden Aufgaben ist richtig gelöst?
Kreuze die zutreffende(n) Antwort(en) an!
(2a + 3b)² = 4a² + 10ab + 9b²
(3x – 5y)² = 9x² – 30xy + 25y²
(4u + 2v)² = 8u² + 16uv + 4v²



(5e – 4f)² = 25e² – 40ef – 16f²

(6m + 3n)² = 36m² + 18mn + 9n²

10) Satzgruppe von Vieta
Bestimme zu jeder Lösungsmenge L die zugehörige quadratische Gleichung!
Aufgabenstellung:
Ordne jeder Lösungsmenge die richtige Gleichung zu!
A
+ 11x + 30 = 0
B
+ 2x - 3 = 0
C
- 8x + 16 = 0
D
- 2x – 1 = 0
E
+ 8x + 16 = 0
F
x – 30 = 0
11) Lösungsfälle mit Parameter
Gegeben ist eine quadratische Gleichung ax2 + 10x – 5 = 0; a
a
Aufgabenstellung:
Gib alle Werte von a an, für die die quadratische Gleichung keine reelle Lösung besitzt!
12) In der folgenden Abbildung sind vier rechtwinklige Dreiecke dargestellt.
Aufgabenstellung:
Gib in jedem Dreieck für den bezeichneten spitzen Winkel an, welche Winkelfunktion durch das
angegebene Seitenverhältnis dargestellt wird. Für das Dreieck 2 ist die Aufgabe gelöst!
a) Dreieck 1: ....... α 
c1
e
c) Dreieck 3: ....... γ  
j
k
b) Dreieck 2: tan (β) =
b
u
d) Dreieck 4: ....... δ  
h2
g3