Geogebra_Aufgabe_5

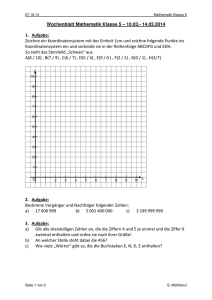
Aufgabe 5
Besondere Punkte im Dreieck: Inkreismittelpunkt
1.
Zeichne drei Punkte A, B, C
2. Verbinde mit richtig bezeichneten Strecken (nach dem gegenüberliegenden Punkt aber als
Kleinbuchstabe benannt). Du musst dazu die Strecken mit der rechten Maustaste anklicken und
„Beschriftung anzeigen“ wählen. Bei falschen Bezeichnungen wähle rechte Maustaste
„Eigenschaften“ und bessere den Namen aus.
3.
Zeichne die Winkelhalbierende von α: Im
vierten Bild von rechts „Winkelsymmetrale“
wählen und jetzt nach der Reihe B, A, und C
anklicken (der Scheitelpunkt mit des Winkels muss
als zweites angeklickt werden!)
4.
Zeichne ebenso die Winkelsymmetralen von β und
γ. Schneide zwei Winkelsymmetralen und
bezeichne den Schnittpunkt mit I
(Inkreismittelpunkt )
Winkel5. Zur Konstruktion des Inkreises hole deinen Lehrer.
symmetrale
(Oder:Du musst dazu von I aus eine Gerade im rechten Winkel
auf eine Seite zeichnen, Gerade und Seite schneiden, jetzt hast du einen Punkt im richtigen
Abstand Radius des Inkreises mit Mittelpunkt I)
6.
Speichere jetzt die Datei
unter
Vorname_Klasse_Aufgabe5.
ggb am Desktop
Achtung: Vor Unterrichtsende
solltest du alle deine Dateien in den
Ordner
\berta\workdir\3ef_2013\uerad29.1
0.\ergebnisse\3e oder 3f kopieren
und am Desktop löschen!