Temperaturabhängigkeit der Beweglichkeit Feldabhängigkeit der

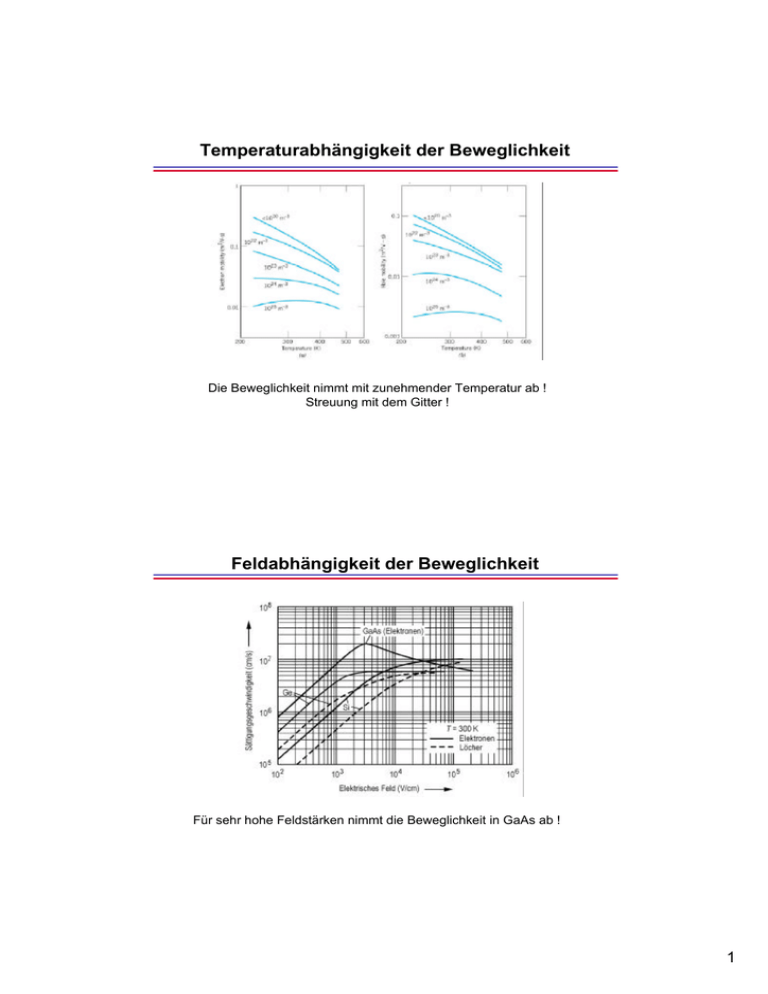
Temperaturabhängigkeit der Beweglichkeit
Die Beweglichkeit nimmt mit zunehmender Temperatur ab !
Streuung mit dem Gitter !
Feldabhängigkeit der Beweglichkeit
Für sehr hohe Feldstärken nimmt die Beweglichkeit in GaAs ab !
1
Feldabhängigkeit der Beweglichkeit
Für sehr hohe Feldstärken nimmt die Beweglichkeit in GaAs ab !
Elektronen gehen in die L- und X-“Täler“
Es bilden sich Bereiche mit langsamen Elektronen, gewissermassen ein
Elektronenstau. Führt zum sogenannten Gunn-Effekt !
Ausnutzung in der Gunn-Diode.
Welche Zustände sind denn eigentlich besetzt ?
2
Welche Zustände sind denn eigentlich besetzt ?
-im Prinzip sollte das Ganze
ähnlich wie beim Atom erfolgen
- Besetzung von „unten nach oben“
-...wie viele Elektronen kann
man in
ein Band hineinsetzen ?
...
Zustandsdichte für Elektronen
•
Gesucht ist die Dichte der Zustände in einem Kristall
•Gedankenexperiment: Wir betrachten einen Würfel der Kantenlänge
Lx=LY=LZ=L und fordern als Randbedingung für die Elektronenwellen
Ψ, dass diese sich periodisch fortsetzen.
....
....
Lx
Für die Wellenfunktion muss gelten:
Die Blochwelle kann geschrieben werden als:
rr
r
r
Ψ nk (r ) = eikr unkr ( r )
3
Zustandsdichte für Elektronen
....
....
Lx
rr
r
r
Ψ nk (r ) = eikr unkr ( r )
Die Funktion u(r) ist sowieso periodisch auf einer Elementarzelle,
also müssen wir nur k so wählen, dass exp(ikr) periodisch mit der Periode
Lx ist:
Damit ergeben sich die erlaubten
Wellenvektoren:
Zustandsdichte für Elektronen
– Aufgrund der periodischen
Randbedingung sind nur diskrete
Energiezustände erlaubt.
– Die Wahl von L beeinflusst das
Ergebnis nicht, da wir später durch
das Volumen teilen.
4
Zustandsdichte für Elektronen
... bzw. in 2D
d.h.
pro k-Zustand ein „Volumen“
von
 2π 
 L 


3
Idee: Zähle zunächst die
Zustände im k-Raum
Zustandsdichte im k-Raum
•
Die Anzahl der Zustände N(k)·∆k
in einer Schale der Dicke ∆k im
k-Raum ist („Volumen“ der
Schale geteilt durch „Volumen“
eines Zustandes, ·2 wegen Spin):
5
Zustandsdichte ρe(W)
•
Transformation von der k-Abhängigkeit zur Energieabhängigkeit:
Aus E = W =
h2k 2
h2k
h2k
folgt dW =
dk bzw. ∆W=
∆k
2m
m
m
Für die Anzahl der Zustände in einem Energieintervall ∆W um W
ergibt sich dann:
•Damit ist die auf das Volumen V normierte Zustandsdichte ρe(W):
Parabelnäherung
Direkter Halbleiter
z.B. GaAs
Indirekter Halbleiter
z.B. Si, Ge
Wie sieht das dann konkret im Fall von parabolischen Bändern aus ?
Hier ist der Bezugspunkt für die Energie das Minimum des
Leitungsbandes W L bzw. das Maximum des Valenzbandes W V.
6
Zustandsdichte in der Parabelnäherung
•
In der Parabelnäherung verhalten sich Elektronen im LB quasifrei mit
der effektiven Masse mn. Ihre Zustandsdichte ist gegeben durch:
•
In der Parabelnäherung verhalten sich Löcher im VB quasifrei mit der
effektiven Masse mp. Ihre Zustandsdichte ist gegeben durch:
Äquivalente Zustandsdichten
•
Die Vorfaktoren werden oft in den effektiven Zustandsdichten NL und
NV zusammengefasst:
Die energieabhängige Zustandsdichte ergibt sich dann gemäß
7
Zusammenfassung Parabolische Bänder
Dispersionsrelation
Zustandsdichte
Zustandsdichte : Badewannen-Analogie
•
•
•
•
Wie viel Wasser ist in einer Badewanne, die bis zur Höhe von 30 cm über
dem Boden gefüllt ist?
Wie viele Liter passen in die nächsten 10 cm?
Die Antwort hängt von der Form der Badewanne ab!
Integrieren ergibt Gesamtwassermenge.
Höhe
Liter Wasser
pro cm Höhe
8
Zustandsdichte in Kristallen
•
•
•
Die Wassermenge in einer bis zu einer bestimmten Höhe gefüllten
Badewanne hängt von der Form der Badewanne ab.
Genauso hängt die Anzahl der Ladungsträger in einem bis zu einer
bestimmten Energie gefüllten Band von der Form der Bandstruktur
ab.
Die Anzahl der erlaubten Zustände pro Volumeneinheit und pro
Energieintervall ist durch die Zustandsdichte ρ(W) gegeben.
Höhe
W
ρ(W)
Liter Wasser
pro cm Höhe
Besetzung der Bänder
•
Bei T = 0 K sind alle Zustände im Valenzband (VB) mit Elektronen
besetzt und alle Zustände im Leitungsband (LB) sind unbesetzt.
•
Bei steigender Temperatur T beobachtet man, dass mehr und mehr
Zustände im Leitungsband besetzt sind und mehr und mehr Zustände
im Valenzband frei sind.
– Leitfähigkeit σ = 0, da es keine beweglichen Ladungsträger gibt.
– Da es mehr bewegliche Träger gibt, steigt die Leitfähigkeit zunächst mit
der Temperatur.
•
Wie können wir die Besetzung der Zustände berechnen ???
T=0K
T = 150 K
T = 300 K
LB
LB
LB
VB
VB
VB
9
Wie kommen Elektronen ins LB?
•
Elektronen können vom Valenzband (VB) ins Leitungsband (LB) übergehen,
wenn ihnen mindestens die Energie W G zugeführt wird.
– Quantenmechanisch gesehen geht das Elektron durch Energiezufur von einem
Zustand im Valenzband in einen Zustand im Leitungsband über.
•
Die Energie kann auf verschiedene Arten zugeführt werden:
–
–
–
–
Thermische Energie (Stoß mit dem „wackelnden“ Atomgitter)
Elektromagnetische Strahlung
Elektrische Felder
W
…
LB
WG
VB
x
Quantenstatistik
Warum befinden sich bei höheren Temperaturen eigentlich Elektronen
in höheren Niveaus ?
Aus der Thermodynamik:
Die Besetzung der Zustände erfolgt so,
dass die freie Energie minimiert wird:
F=U-TS=Min!
Innere Energie U = ∑ ni Ei
i
10
Quantenstatistik
F=U-TS=Min!
2
S = k ln P
Für die Entropie gilt:
1
Hierbei ist P die Anzahl der Realisierungsmöglichkeiten.
Nehmen wir an, wir hätten 6 Elektronen auf zwei Energieniveaus 1 und 2
zu verteilen:
2
Wenn alle Elektronen im Zustand 1
sind, gibt es nur eine einzige
Realisierungsmöglichkeit.
S=0
1
Das ist der
Zustand für T=0.
Quantenstatistik
2
2
2
2
2
2
1
1
1
1
1
1
Der Zustand (5 e‘s in 1, und 1 e in 2) lässt sich mehrfach realisieren.
D.h. seine Entropie S=k lnP ist endlich.
F=U-TS=Min!
Je höher die Temperatur ist, desto stärker sorgt die damit verbundene
Entropieerhöhung für eine Besetzung der höheren Zustände.
Obwohl die innere Energie größer wird, wird u. U. die freie Energie kleiner !
11
Quantenstatistik
..
Formalerer Weg:
i+1
i
Zustand i
Energie Ei
Anzahl der Zustände gi
..
Minimierung der freien Energie
(bei festgehaltener Teilchenzahl):
δF = ∑
i
∂F
δ ni = 0; wobei
∂ni
∑δ n
i
=0
i
D.h. die Besetzung muss sich so einstellen, dass für beliebige i und k gilt:
∂F
∂F
δ nk +
δ ni = 0 wobei δ nk = −δ ni
∂nk
∂ni
Daraus folgt:
∂F
∂F
=
∂nk ∂ni
F=U-TS=Min!
Quantenstatistik
Wie gross ist die Entropie ?
..
i+1
i
Zustand i
Energie Ei
Anzahl der Zustände gi
..
Anzahl der Realisierungsmöglichkeiten von ni Elektronen im Zustand i:
Zunächst:
g i (g i − 1)(g i − 2)...(g i − ni + 1) =
gi !
(g i − ni )!
Es muss allerdings noch berücksichtigt werden,
dass die Elektronen ununterscheidbar sind.
Damit ergibt sich als Anzahl der Realisierungsmöglichkeiten für das Niveau i:
Pi =
gi !
1
(g i − ni )! ni !
12
Quantenstatistik
Für das gesamte System ergibt sich dann als Anzahl der Realisierungsmöglichkeiten
P = ∏ Pi = ∏
i
i
gi !
1
(g i − ni )! ni !
Für die Entropie ergibt sich damit:
S = k ln P = k ∑ [ln g i !− ln ni !− ln((g i − ni )!]
i
Für grosse n kann die Stirling‘sche Formel für n! eingesetzt werden:
ln n ! ≈ n ln n − n
Damit folgt:
∂F
∂ 

=
µ=
∑ ni Ei − kT ∑ [ g i ln gi − ni ln ni − (g i − ni )ln(g i − ni )]
∂nk ∂nk  i
i

nk
... = Ek + kT ln
g k − nk
Quantenstatistik
und es ergibt sich:
µ=
∂F
∂ 

=
∑ ni Ei − kT ∑ [ g i ln g i − ni ln ni − (g i − ni )ln(g i − ni )]
∂nk ∂nk  i
i

nk
... = Ek + kT ln
g k − nk
Für die Besetzung des Zustandes i gilt also im
thermodynamischen Gleichgewicht:
ni = g i
1
E −µ
1 + exp( i
)
kT
Die Wahrscheinlichkeit, dass ein
quantenmechanischer Zustand der
Energie E bei gegebener Temperatur
besetzt ist, ist damit
f (E ,T ) =
1
E−µ
1 + exp(
)
kT
Fermi-Dirac-Verteilung
13
Fermi-Dirac-Verteilung
f (E ,T ) =
1
E−µ
1 + exp(
)
kT
µ ist das chemische Potential
Bei der T=0K ergibt sich eine Stufenfunktion.
µ wird meistens
als
Fermienergie EF(W F)
bezeichnet.
Vergleich Fermi- und Boltzmann-Verteilung
•
Da bei Halbleitern die Fermienergie EF oft in der Bandlücke liegt, kann
oft die Boltzmann-Verteilung verwendet werden.
14
Anzahl der Ladungsträger
•
•
•
•
Jetzt wissen wir, mit welcher Wahrscheinlichkeit f(W) ein Zustand im
thermischen Gleichgewicht mit einem Elektron besetzt ist.
Um die Anzahl der Ladungsträger zu berechnen müssen wir nur noch
wissen, wie viele Zustände es insgesamt gibt.
Die Anzahl der erlaubten Zustände pro Volumeneinheit und pro
Energieintervall nennt man die Zustandsdichte ρ(W).
Die Anzahl der Elektronen im Leitungsband
(bzw. die Anzahl der Löcher im Valenzband)
mit einer Energie W ist im thermischen
Gleichgewicht gegeben durch:
W
LB
WF
•
Durch Integrieren über alle Energien W erhält
man die Gesamtzahl der Ladungsträger n
bzw. p.
VB
x
Anzahl der Ladungsträger bei Energie W
•
Für die Anzahl der Ladungsträger gilt damit:
15
Gesamtzahl der Ladungsträger
•
Die Gesamtdichte der beweglichen Ladungsträger im thermischen
Gleichgewicht erhält man durch Integration über alle Energien
•
Die äquivalenten Zustandsdichten sind also Zustandsdichten, die man sich
unmittelbar an den Bandkanten lokalisiert vorstellen kann.
Eigenleitungsträgerdichte
•
Da im Halbleiter Elektronen im LB und Löcher im VB paarweise
entstehen gilt:
•
•
ni nennt man die Eigenleitungsträgerdichte.
Berechnung des Produktes ergibt:
•
Wir sehen, dass die Ladungsträgeranzahl ni im thermischen
Gleichgewicht vom Bandabstand W G, den effektiven Massen der
Bänder und der Temperatur abhängt.
– Für entartete Halbleiter (Boltzmann-Näherung gilt nicht) hängt sie auch
von der Fermienergie W F ab.
16
Temperaturabhängigkeit von ni
•
•
Für T = 293 K (Raumtemperatur)
ist W th = kT = 25 meV.
W G ≈ 1 eV = 40 W th.
Ende 15.12.03
Source:[3]
17