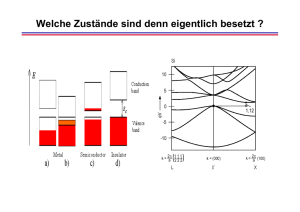
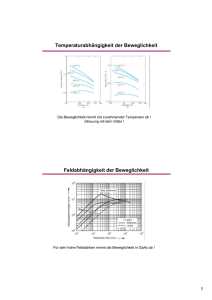
Vorwort

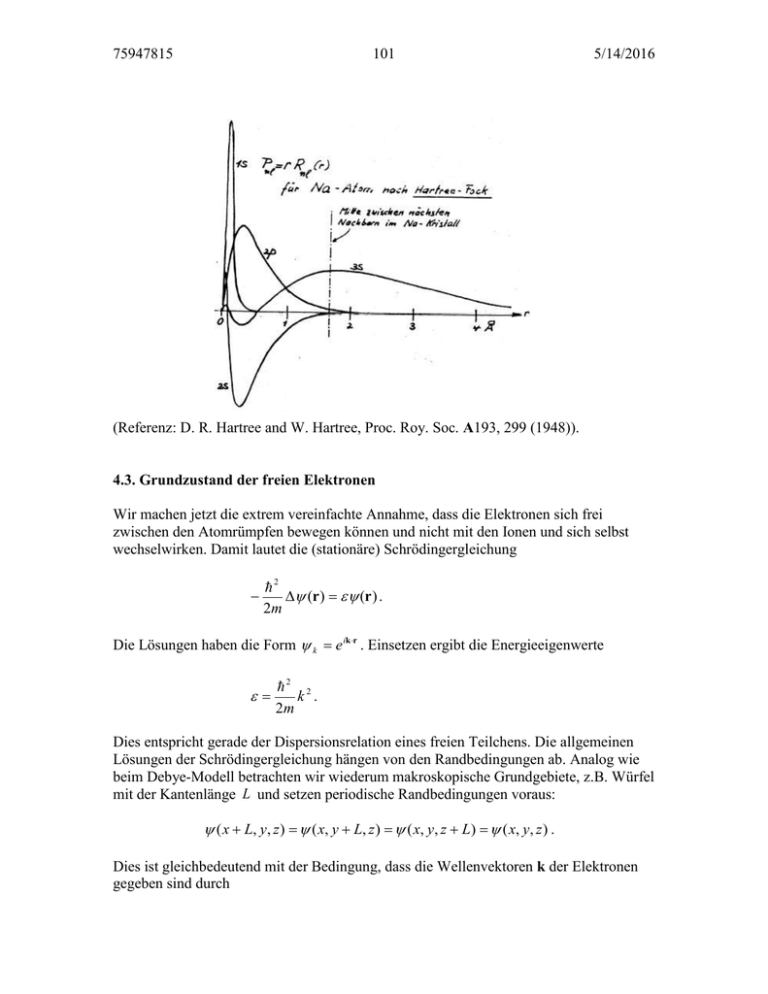
75947815
101
5/14/2016
(Referenz: D. R. Hartree and W. Hartree, Proc. Roy. Soc. A193, 299 (1948)).
4.3. Grundzustand der freien Elektronen
Wir machen jetzt die extrem vereinfachte Annahme, dass die Elektronen sich frei
zwischen den Atomrümpfen bewegen können und nicht mit den Ionen und sich selbst
wechselwirken. Damit lautet die (stationäre) Schrödingergleichung

2
 (r )   (r ) .
2m
Die Lösungen haben die Form  k  e ikr . Einsetzen ergibt die Energieeigenwerte

2 2
k .
2m
Dies entspricht gerade der Dispersionsrelation eines freien Teilchens. Die allgemeinen
Lösungen der Schrödingergleichung hängen von den Randbedingungen ab. Analog wie
beim Debye-Modell betrachten wir wiederum makroskopische Grundgebiete, z.B. Würfel
mit der Kantenlänge L und setzen periodische Randbedingungen voraus:
 ( x  L, y, z )   ( x, y  L, z )   ( x, y, z  L)   ( x, y, z ) .
Dies ist gleichbedeutend mit der Bedingung, dass die Wellenvektoren k der Elektronen
gegeben sind durch
75947815
102
k x  nx
5/14/2016
2
2
2
, k y  ny
und k z  n z
.
L
L
L
Die Elektronen haben die Energien
2 2

k
2m
 2  2
2
2
k 
 (n x  n y  n z ) .
 L 
2
mit
2
Jedem Einelektronen-Zustand mit dem Zahlentripel (n1 , n2 , n3 ) einspricht ein Zustand mit
dem Volumen (2 / L) 3 im k-Raum. Die Zahl der Zustände in einem nicht zu kleinen
Volumenelement d 3 k beträgt
dZ 
d 3k
L3
V

d 3k 
d 3k .
3
3
3
(2 / L)
(2 )
(2 )
Die Zustandsdichte im k-Raum ist also V /( 2 ) 3 . Das Grundgebiet V enthält N
unabhängige Elektronen die durch N Einteilchenwellenfunktionen beschrieben werden.
Aufgrund des Pauli-Prinzips kann jeder Zustand doppelt besetzt werden, nämlich mit
Spin-up und Spin-down ( ms   12 ).
Im Grundzustand (= Zustand tiefster Energie) ergibt sich die elektronische Energie durch
die lückenlose Besetzung der tiefstliegenden Zustände im k-Raum. Die Zustände liegen
innerhalb einer Kugel deren Radius der Bedingung genügen muss
N 2
V 4 3
V 3
kF 
kF .
3
(2 ) 3
3 2
Mit der Elektronendichte n  N / V erhält man für den Radius dieser sogenannten FermiKugel den Fermi-Radius
k F  (3 2 n)1 / 3 .
Die Fermi-Energie ist gegeben durch
F 
2 2 2
kF 
(3 2 n) 2 / 3 .
2m
2m
Beachte, dass bei der Wahl eines “Fermi-Würfels” ein Zustand höherer Energie erhalten
würde.
75947815
103
5/14/2016
Grössenordnung der Fermi-Energie für ein einfaches Metall wie Na:
In Natrium ist die Anzahl der Leitungselektronen n ungefähr gleich der Anzahl der
Atome. Aus der Dichte und dem Atomgewicht erhält man n  2.65  10 22 cm-3. Damit
ergibt sich



k F  9.22  10 7 cm-1
F  2 / k F  6.81 Å
 F  5.2  10 19 J  3.24 eV .
Die Fermi-Energie entspricht einer Temperatur TF   F / k B  38000 K! TF ist mehr als
ein Faktor 100 mal höher als die Raumtemperatur (293 K). Man sagt, dass das
Elektronengas entartet ist. Vergleich mit den Gitterschwingungen: Phononenzustände
sind nur bis ungefähr Raumtemperatur besetzt (Bose-Teilchen). Elektronen (FermiTeilchen) besetzen bereits bei T  0 Energieniveaus mit viel höheren Energien.
Die Gesamtenergie der Elektronen am absoluten Nullpunkt erhält man durch Summation,
beziehungsweise Integration, im k-Raum
Etot
2 2
2k 2 V
2 V
3
 2
k 2 
d
k

2
2m (2 ) 3
2m (2 ) 3
k  k F 2m
Fermi
kF
2 V
k
4

k
dk

0
m 2 2
2
2
kF
k
4
dk
0
Kugel
Etot 
Zusammen mit N 
 2V k F5
V 3 2 2

kF 
kF .
2m
2 2 m 5 5 2
V 3
k F erhält man für die Energie pro Elektron
3 2
Etot 3  2 2 3
 el 

kF   F .
N
5 2m
5
Analog wie bei den Phononen berechnen wir jetzt die Energie-Eigenwertdichte  ( ) .
Aufgrund der Dispersionsrelation für freie Elektronen
2 2

k
2m
1/ 2
1/ 2
1  2m 
 2m 
erhält man k   2   1 / 2 und dk   2   1 / 2 d . Zusammen mit der
2  
 
3
Zustandsdichte im k -Raum V (2 ) ergibt sich
V
V 2m 1  2m 
 ( )d 
4k 2 dk 

  2 
3
2  
(2 )
2 2  2
1/ 2

1 / 2
V  2m 
d 


(2 ) 2   2 
3/ 2
 1 / 2 d .
75947815
104
5/14/2016
Damit erhält man für die Zustandsdichte für freie Elektronen in einem Grundgebiet mit
dem Volumen V
V  2m 
 ( ) 


(2 ) 2   2 
3/ 2
 1/ 2 .
Beachte, dass die der Faktor zwei wegen den zwei möglichen Spinorientierungen  12
nicht in  ( ) enthalten ist.
Eine etwas heuristische Bemerkung zur Zustandsdichte:
Die Heisenberg’sche Unschärferelation lautet in einer Dimension:
x   p  h .
h
k  k ):
Umgeschrieben in Wellenvektoren ( p 
2
x  k
 1.
2
In differentieller Schreibweise ergibt sich in d Dimensionen die Beziehung
dr d dk d
 1.
(2 ) d
Dieses Ergebnis besagt, dass pro Einheitszelle im 2d -dimensionalen (r , k ) -Raum ein
Zustand vorhanden ist. Die Gesamtzahl der Zustände erhält man durch Integration über
den r -Raum und den k -Raum:
N
1
(2 ) d

dr d dk d .
r  Raum
k  Raum
Für einen Würfel ist die Integration über den direkten Raum trivial und wir erhalten
N
Ld
(2 ) d

dk d .
k  Raum
Damit können wir die bisherigen, langwierigen Diskussionen über die Quantisierung im
k-Raum etc. im wesentlichen umgehen. Im weiteren können wir leicht Zustandsdichten
in beliebig dimensionalen Räumen berechnen. Wenn wir die Zustandsdichte der Energie
75947815
105
5/14/2016
berechnen wollen, geht die Dispersionsrelation der Anregungen bei der Umformulierung
von k -Einheiten in Energieeinheiten ein.
Die Fortsetzung dieser Vorlesung wurde von Dr. Hans-Benjamin Braun gemacht
(siehe PDF File)