Physik 10

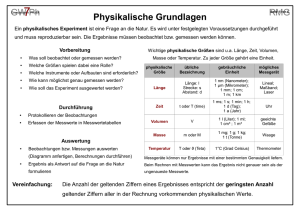
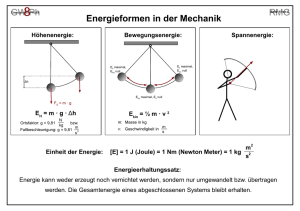
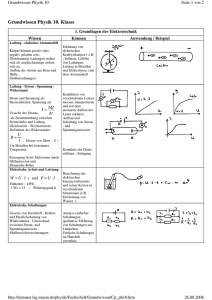
GW
10Ph
Grundwissen Physik
RMG
Seite 1 von 6
Astronomische Weltbilder und Keplersche Gesetze
Heliozentrisches Weltbild
●
Die Sonne steht im Mittelpunkt unseres Sonnensystems,
die Planeten umkreisen sie.
●
Viele Planeten werden von Monden umkreist.
●
Die Sterne sind viele Lichtjahre von uns entfernt und
bilden Galaxien, zum Beispiel unsere Milchstraße.
Δt
A1
Sonne
A2
Δt
Die Keplerschen Gesetze
1. Die Planetenbahnen sind Ellipsen, in deren einem
Brennpunkt die Sonne steht.
2. Der von der Sonne nach einem Planeten gezogene
Ortsvektor überstreicht in gleichen Zeiten Δ t gleiche
Flächen A1 und A2.
3. Die Quadrate der Umlaufzeiten T zweier Planeten
um denselben Zentralkörper verhalten sich wie die
dritten Potenzen der großen Halbachsen a ihrer
Bahnellipsen:
2
T1
2
T2
3
=
a1
3
a2
T1, T2 Umlaufzeiten, a1, a2 große Bahnhalbachsen.
Sonne
a1
a2
Planet 1
Planet 2
GW
10Ph
Grundwissen Physik
RMG
Seite 2 von 6
Die Mechanik Newtons – Teil 1
Waagrechter Wurf (reibungsfrei)
Erhaltungssätze
Energieerhaltungssatz:
x( t )  v 0  t;
In einem abgeschlossenen System (kein Eingriff von
außen) bleibt die Gesamtenergie erhalten.
●
y(t )   12 g  t 2
v0
Gleichförmige Bewegung
in horizontaler Richtung mit
Impuls:
p=m·v
Abwurfgeschwindigkeit v0.
●
Einheit:
[p] = 1 Ns = 1 kg · m/s
Beschleunigte Bewegung
in vertikaler Richtung mit der
Fallbeschleunigung g = 9,81 m/s2.
Impulserhaltungssatz: In einem abgeschlossenen
System bleibt der Gesamtimpuls erhalten.
Gravitationsgesetz
p1 + p2 + … + pn = p1' + p2' + … + pn'
Massen ziehen sich gegenseitig an. Für die
Anziehungskraft zweier kugelförmiger Körper der Massen
Für einen geradlinigen zentralen Stoß mit zwei
m und M mit dem Mittelpunktsabstand r gilt:
beteiligten Körpern gilt damit:
m1 v1 + m2 v2 = m1 v1' + m2 v2'
Hierbei ist auf die Vorzeichen der Geschwindigkeiten zu achten!
F  G
m M
r2
wobei G die sog. Gravitationskonstante ist.
GW
10Ph
Grundwissen Physik
RMG
Seite 3 von 6
Die Mechanik Newtons – Teil 2
Harmonische Schwingung
Kreisbewegung
mit konstanter Winkelgeschwindigkeit ω
D: Federhärte
Eine Schwingung, bei der die
Rückstellkraft F proportional zur
Winkelgeschwindigkeit:
1
F=-D·y
Auslenkung y ist, nennt man
y: Auslenkung aus Ruhelage
eine harmonische Schwingung.
Einheit [ w ]: 1 s
v = ω ⋅r
r: Bahnradius in m
Zentripetalkraft:
y  A  sin 2T  t   A  sin(  t )
Zentripetalbeschleunigung:
m⋅v
r
a=
v
2
= ω⋅r
r
2
Zentripetalkraft und Zentripetalbeschleunigung sind zum Kreismittelpunkt
y: Auslenkung oder Elongation
A: maximale Auslenkung bzw. Amplitude
T: Schwingungsdauer: Zeit für eine volle Schwingung
hin gerichtet, die Bahngeschwindigkeit zeigt in Richtung der
Kreistangente.
Frequenz: Zahl der Schwingungen pro Zeit
Einheit [f]: 1 Hz (1 Hertz, 1 Hz =
1
s
)
FZ
Es gilt:
f=
1
T
2
FZ =
m: Masse in kg
Schwingungsgleichung:
Δϕ
2π
=
Δt
T
T: Zeit für einen Umlauf in s
Bahngeschwindigkeit:
Beispiel: Federpendel
f:
ω =
GW
10Ph
Grundwissen Physik
RMG
Seite 4 von 6
Wellen
Beachte: Auch wenn Wellen graphisch ähnlich zu
Schwingungen dargestellt werden, so besitzen sie im
Reflexion
Brechung
Einfallswinkel = Reflexionswinkel
Unterschied dazu eine Abhängigkeit sowohl vom Ort x
a
als auch von der Zeit t.
a a'
Transversalwelle (Querwelle)
b
Die Teilchen schwingen senkrecht
Ausbreitungsrichtung
(„quer“) zur Ausbreitungsrichtung
der Welle.
(Bsp. Seilwellen, Wasserwellen)
Schwingungrichtung
Longitudinalwelle (Längswelle)
Die Teilchen schwingen in
Richtung der Ausbreitung
Beugung
Interferenz
Abweichung von der geradlinigen
Überlagerung von Wellenfeldern;
Ausbreitung;
dabei können u.a. die Wellen
Folge: Wellen können sich hinter
verstärkt (konstruktive Interferenz)
Öffnungen und Hindernissen in
oder ausgelöscht (destruktive
den „Schattenraum“ ausbreiten.
Interferenz) werden.
Schwingungrichtung
Ausbreitungsrichtung
der Welle.
(Bsp. Schallwellen)
Wellenlänge λ (z.B. Abstand benachbarter Wellenberge)
Schwingungsdauer T; Frequenz f; es gilt :
Ausbreitungsgeschwindigkeit v:
f=
1
T
v=λ·f
●
Z1
●
Z2
GW
10Ph
Grundwissen Physik
RMG
Seite 5 von 6
Licht
Modellvorstellungen
●
Strahlenmodell:
●
Teilchenmodell (Photonenmodell):
Vorstellung: Ausbreitung des Lichts in Form von
Licht besteht aus einzelnen Energieportionen, den
„Lichtstrahlen“
Photonen.
Energie eines Photons: EPh = h ∙ f
●
Wellenmodell (Licht als elektromagnetische Welle):
Bei Licht treten Beugungs- und Interferenzerscheinungen
h: Plancksche Konstante
f: Frequenz des Lichts im Wellenmodell
auf.
Der Photoeffekt kann mit Hilfe des Teilchenmodells
Beugung und Interferenz am Doppelspalt
gut erklärt werden.
Äußerer Photoeffekt
Trifft energiereiches Licht (f groß) auf bestimmte Metalle,
so kann es aus ihnen Elektronen herauslösen.
An schmalen Spalten und
Hindernissen wird Licht
gebeugt.
Hinter einem Doppelspalt
überlagert sich das gebeugte
Licht. Es tritt Interferenz auf.
Für die Interferenzmaxima gilt: ∆ s = k· 
(k = 0,1, 2,...)
∆ s: Gangunterschied benachbarter Randstrahlen
l: Wellenlänge des Lichts
-
-
-
energiereiches Licht
- - - - - - - - - - -- - - --
GW
10Ph
Grundwissen Physik
Grundaussagen der speziellen Relativitätstheorie
Konstanz der Lichtgeschwindigkeit
Licht breitet sich im Vakuum unabhängig vom Bewegungszustand der
Die Masse eines Körpers ist von seiner Geschwindigkeit abhängig.
m(v) =
Zeitdilatation
m0
√
m0: Ruhemasse des Körpers
2
()
1−
v
c
Energie
Uhren, die sich relativ zu einem Beobachter mit der Geschwindigkeit v
Längenkontraktion
Seite 6 von 6
Massenabhängigkeit
Lichtquelle und des Beobachters immer mit der Geschwindigkeit c aus.
m
Es gilt: c ≈ 3,0 ∙ 10 8
s
schnell bewegen, gehen für diesen Beobachter langsamer.
RMG
E = E0 + Ekin = m ∙ c2
E0 = m0 ∙ c2
Körper, die sich relativ zu einem Beobachter schnell bewegen,
erscheinen für diesen in Bewegungsrichtung verkürzt.
Einblick in die Quantenphysik
●
●
Elektronen, Photonen, Neutronen, Protonen und weitere
Quantenobjekte verhalten sich stochastisch, d.h.
Elementarteilchen, aber auch Atome und Moleküle sind
eine Aussage über das Verhalten eines einzelnen
Quantenobjekte.
Objekts ist nicht möglich, sondern nur eine
Quantenobjekte haben Wellen- und Teilcheneigenschaften.
Wahrscheinlichkeitsaussage, wenn man eine große
Bewegten Quantenobjekten kann keine exakte Bahn zugeordnet
Anzahl von Objekten betrachtet.
werden.
●
●
Ort und Geschwindigkeit sind nicht gleichzeitig genau
bestimmbar (Heisenberg).