Algorithmik II 8. ¨Ubung Aufgabe 20 Graphen Gegeben sei der

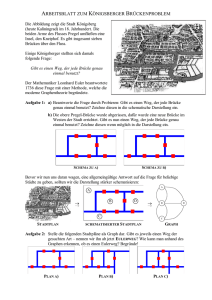
Algorithmik II
Aufgabe 20
8. Übung
Graphen
Gegeben sei der folgende Graph:
3
1
A
A
A
4 A
@ A
@A
@
AU
R
@
-2
- 5 6
a) Geben Sie an, wie der Graph durch eine Adjazenzmatrix und durch Adjazenzlisten gespeichert wird.
b) Bestimmen Sie für den Graphen eine topologische Sortierung.
c) Bestimmen Sie mit Hilfe des Algorithmus zum systematischen Durchlaufen eines Graphen
alle Knoten, die von Knoten 1 aus erreichbar sind. Als Auswahlstrategie soll LIFO verwendet
werden.
Rechnerübung 15
Graphen
a) Schreiben Sie eine Klasse AdjList, die es Ihnen ermöglicht, einen gerichteten Graphen
in einer Adjazenzliste zu speichern sowie eine Klasse AdjMatrix, mit der ein gerichteter
Graph durch eine Adjazenzmatrix gespeichert werden kann. Dem Kontruktor beider Klassen
soll jeweils die Anzahl der Knoten des Graphen als Parameter übergeben werden. Die Speicherung der von den einzelnen Knoten ausgehenden Kanten soll in der Klasse AdjList mit
Hilfe einer verketteten Liste realisiert werden.
Weiterhin sollen beide Graphen eine Methode insertEdge(int from, int to) zur
Verfügung stellen, mit der Sie eine Kante vom Knoten from zum Knoten to einfügen
können. Dabei soll die Benennung der Knoten bei 1 beginnen.
Implementieren Sie auch die Methode toString() für beide Klassen.
b) * Schreiben Sie für die Klasse AdjMatrix eine Methode AdjMatrixToAdjList(),
die ein der Matrizendarstellung entsprechendes AdjList-Objekt zurückliefert sowie für die
Klasse AdjList eine Methode AdjListToAdjMatrix().
c) Schreiben Sie für die Klasse AdjList eine Methode topologicalSort(), die die topologische Sortierung des Graphen unter Verwendung des in der Vorlesung vorgestellten verbesserten Algorithmus zum topologischen Sortieren ausgibt. Weiterhin soll die Methode ausgeben, ob der Graph zyklenfrei ist.
Testen Sie Ihre Implementierung anhand einiger Beispiele aus der Vorlesung.
16. Juni - 20. Juni 2003
-1-
Sommersemester 2003