2015_07_02, Zuordnungen (14), Mind

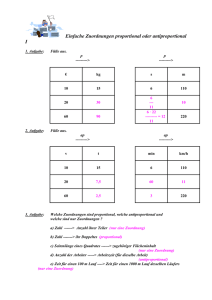
Do, 02.07.2015
Thema:
Zuordnungen: Mind-Map
Besprechung:
 Unterschriebene Arbeiten abgeben, es fehlen noch 16 11 6(!)

Wiederholungen
 Welche Bedeutung hat der Begriff „Quotientengleichheit“ in Bezug auf Zuordnungen?
 Welche Bedeutung hat der Begriff „Produktgleichheit“ in Bezug auf Zuordnungen?
 Ergänze die Tabellen der antiproportionalen Zuordnungen.
o
Formuliere zunächst eine Dreisatzaufgabe
Anzahl
Gläser
Füllmenge
(in l)
200
0,2
0,5
o Die Zuordnungsvorschrift lautet:
X
o
Hausaufgabenkontrolle
1. AH, S. 53, Drei Werte sind gegeben – Dreisatz (2) Rest vom AB „Diplom“
2. AB Rechnen mit antiproportionalen Zuordnungen (Dreisatz)
Nr. 1.1, 2.1, 3.1 (Selbstkontrolle, durch Lösungswolken), Kastenaufgaben
3. AB Rechnen mit proportionalen Zuordnungen (Dreisatz)
a. Nr. 1.1, 2.1, 3.1 (Selbstkontrolle, durch Lösungswolken) , Kastenaufgaben
D:\481341462.doc
Themen: Eine Mind-Map (Gedächtniskarte) zum Thema Zuordnungen
1. „Eine Mind-Map (englisch: mind map; ..... ,Gedächtnis[land]karte) beschreibt eine von Tony
Buzan geprägte ....... Technik, die man z. B. ......... für Mitschriften nutzen kann.“
(aus: Wikipedia, 1.7.2015)
2. Anwendung einer Mind-Map für Prüfungsvorbereitung
„Für die Prüfungsvorbereitung ist das Mind-Mapping gut geeignet, da in kreativen Schritten eine
griffige Darstellung des Lernstoffes erarbeitet wird und später weiter durch systematisch
wiederholte Beschäftigung mit dieser Wiedergabe der gelernte Stoff gefestigt wird. Eine solche
übersichtliche Anordnung der semantischen Struktur des Wissens fördert die stabile
Erinnerbarkeit über lange Zeiträume. Beim Aufbau der Mind-Maps sollten einem Ast nicht mehr
als sieben Unteräste zugeordnet werden. Dies fördert, dass man sich die Mind-Maps während des
Lernens fotografisch merkt und in der Prüfungssituation in Gedanken systematisch durchgeht. So
lassen sich auch umfangreiche Informationen wie Vorlesungsskripte und Ähnliches
reproduzieren.“
(aus: Wikipedia, 1.7.2015)
3. Ein Beispiele:
D:\481341462.doc
4. Tipps zum Mind-Mapping
5. AB Mit einem Mind-Map ein Thema im Gedächtnis behalten
D:\481341462.doc
Name:
Datum:
AB Mit einem Mind-Map ein Thema im Gedächtnis behalten
Das obige Mind-Map bietet einen Überblick über die Lerneinheiten des Kapitels „Zuordnungen“ (Kapitel V im
Schülerbuch). Bisher sind lediglich das Thema und die Hauptäste angelegt.
1. Übertrage zunächst das Mind-Map auf ein unliniertes großes Blatt Papier.
2. Vervollständige die Mind-Map (Gedächtniskart)
3. Denke daran, dass in einem Mind-Map Begriffe, Formeln, Zeichnungen und Beispiele vorkommen können.
Beispiel:
Der erste Hauptast trägt den Überbegriff
Zuordnungen.
Zunächst könntest du ein paar Beispiele für
Zuordnungen anfügen.
Im nächsten Schritt könntest du ergänzen, wie
Zuordnungen dargestellt werden können.
Tipp: Versuche zusätzlich zu den Begriffen Beispiele und Skizzen bzw. Zeichnungen in dein Mind-Map einzufügen.
D:\481341462.doc
Hausaufgaben:
1. Bringe alle deine Hefte mit, in denen du etwas zum Thema Zuordnungen notiert hast.
2. Arbeite an deiner Mind-Map, indem du je ein Beispiel für eine proportionale und eine
antiproportionale Zuordnung hinzufügst (Textform bzw. Sachverhalt, Zuordnungsvorschrift,
Tabelle, Graph)
D:\481341462.doc
Wiederholungen
 Wertetabelle einer proportionalen Zuordnung ausfüllen:
x
0
1,5
3
6
9
15
6
 Wie lautet die Zuordnungsvorschrift?
x  ________
 Gib den Proportionalitätsfaktor an: ___________
 Ist die folgende mathematische Aussage wahr oder falsch? Jede Je-mehrdesto-mehr-Zuordnung ist eine proportionale Zuordnung.
 Wie sieht der Graph einer proportionalen Zuordnung immer aus?

Auf welchen Sachverhalt könnte sich die proportionale Zuordnung beziehen?
Welche Bedeutung hätte dann der Proportionalitätsfaktor?
 Wertetabelle einer proportionalen Zuordnung ausfüllen:
x
0
1,5
3
6
9
10
12
 Wie lautet die Zuordnungsvorschrift?
x  ________
 Gib den Proportionalitätsfaktor an: ___________
 Ist die folgende mathematische Aussage wahr oder falsch? Jede
proportionale Zuordnung ist eine Je-mehr-desto-mehr-Zuordnung.
 Auf welchen Sachverhalt könnte sich die proportionale Zuordnung
beziehen? Welche Bedeutung hätte dann der Proportionalitätsfaktor?
D:\481341462.doc
g
€
8
32
68
Um welchen Sachverhalt könnte es sich hier handeln?
Formuliere zu diesem Sachverhalt und dieser Tabelle eine Dreisatzaufgabe.
Berechne.
Wie groß ist der Proportionalitätsfaktor? Welche Bedeutung hat er?
Anzahl von Helfern für Benötigte Zeit
ein Festaufbau
(in min)
40
120
16
 Um welchen Sachverhalt könnte es sich hier handeln?
 Formuliere zu diesem Sachverhalt und dieser Tabelle eine Dreisatzaufgabe.
 Berechne.
 Weshalb nennt man die Wertepaare antiproportionale Zuordnungen „produktgleich“`?
 Wie groß ist der „ap-Faktor“?
Welche Bedeutung hat dieser Wert?
 Sei 400 sei der „ap-Faktor“einer antiproportionalen Zuordnung. Wie lautet dann die zugehörige
Zuordnungsvorschrift?
D:\481341462.doc
 Ergänze die Tabellen der antiproportionalen Zuordnungen.
Länge
(in cm)
Breite
(in cm)
Produkt
______ · ______
30
600
40
100
Die Zuordnungsvorschrift lautet:
X
D:\481341462.doc