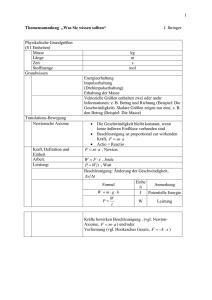
Ideales Gasgesetz

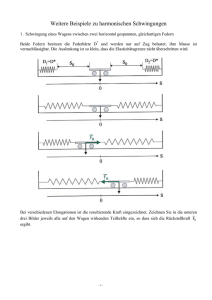
Zusammenfassung wichtiger Begriffe und Übungen zu den
Schwingungen
Die Schwingungsbewegung lässt sich durch die y-Projektion (Schattenbild) einer Rotation
darstellen.
Damit eine Rotation eine Schwingung darstellt, müssen zwei Bedingungen erfüllt sein.
1. Die Winkelgeschwindigkeit des Zeigers der Rotation muss folgenden Betrag haben:

k
m
k..Federhärte des Systems; m…Masse des schwingenden Punktes
2. Der Radius der Rotation muss der Amplitude (maximale Auslenkung) der Rotation
entsprechen.
r=x0.
Für die momentane Position des schwingenden Punktes errechnet man den passenden
Phasenwinkel =0+t und bestimmt die Projektion des Zeigers.
x(t)=rsin=x0sin; v(t)=v0cos=x0cos; a=2x0sin, F=m2x0sin.
Folgende Begriffe beschreiben das zeitliche Verhalten einer Schwingung:
1.Periodendauer T
Die Periodendauer T einer Schwingung ist die Zeitdauer für eine Hin- und Herschwingung.
In dieser Zeitdauer legt der veranschaulichende Zeiger den Phasenwinkel 2π zurück.
Also:
ωT=2π  T=2π/ω
2.Frequenz f
Die Frequenz f beschreibt die Anzahl der Hin- und Herschwingungen pro Zeit.
Also:
f 
oder
Anzahl der Hin  und Herschwing ungen
Zeit
f  t  Anzahl der Hin  und Herschwing ungen
Innerhalb einer Hin- und Herschwingung rotiert der Zeiger einmal.
Hier vergeht aber gerade genau die Periodendauer T!
Daher: f T  1
oder:
f 
1
T
1
1.) Welche Winkelgeschwindigkeit hat ein Zeiger, der die zu folgender Schwingung
dazugehörige Winkelgeschwindigkeit besitzt? k=10N/m, m=2kg.
2.) Die Masse einer Federschwingung wird verdoppelt. Wie ändert sich dann die Frequenz f?
3.) Welche Auslenkung hat die Masse=1kg einer Federschwingung mit der Periodendauer
T=2s und der Amplitude von 0,1m nach 3,3s, wenn die Bewegung aus der Ruhelage
startet? Wie groß ist die Federhärte? Wie groß ist die Geschwindigkeit nach dieser Zeit?
4.) Eine Masse wird in einem Federsystem bei einer Auslenkung von 0,5m losgelassen. Die
Federhärte beträgt 10N/m und die Masse m=2kg. Welche Auslenkung hat die Masse nach
10,5s? Wie groß ist dann die Geschwindigkeit? (Hinweis: Zur Zeit t=0 beträgt der
Phasenwinkel bereits /2!)
5.) Welche Kraft wirkt auf eine Masse an einer Feder mit der Federhärte k=5N/m, wenn die
Frequenz der Federschwingung 10Hertz beträgt nach einer Zeit von 0,45s? Die Amplitude
beträgt 0,1m. Einmal erfolgt der Start aus der Ruhelage und einmal aus dem
Umkehrpunkt.
6.) Mit welcher Frequenz schwingt ein Tauchschwinger, wenn er einen Durchmesser von
1cm hat und die Gesamtmasse 15g beträgt? In welcher Wassertiefe befindet sich die
Ruhelage?
7.) Welche Auslenkung erreicht ein Federpendel, wenn es in der Ruhelage die
Geschwindigkeit v0=10m/s besitzt. k=10N/m, m=1kg.
8.) An einer reibungsfrei drehbar gelagerten
Stange befindet sich eine Masse von 3kg,
die 3m vom Lager entfernt ist. Im
Abstand von 1m vom Lager greift eine
Feder mit k0=1000N/m an.
Wie weit ist die Feder gedehnt. Wie groß ist
die Schwingungsdauer der Anordnung?
(Hinweis: Für die Definition der Federhärte betrachte die zusätzliche Kraft F0 der Feder
am Aufhängungspunkt, die durch die Dehnung der Feder um y0 entsteht. So definierst du
D0. Bestimme so auch die Federhärte am Ort der Masse m!)
9.) Ein Wagen der Masse m=50g ist zwischen 2 Federn gespannt. Die Federhärte k des
Systems beträgt k=10N/m. Die Anfangsauslenkung beträgt 10cm. Nun wirkt innerhalb
einer Periodendauer T auf die Masse eine konstante Kraft F=0,1N über eine Strecke von
1cm.
a) die Kraft wirkt gegen die Bewegung
b) die Kraft wirkt in Bewegungsrichtung
Berechne für a) und b) die Amplitude nach 10 Schwingungen!
10.) Unten ist das Kraft-Auslenkungsdiagramm eines Federpendels dargestellt. Die Masse
sei 1kg.
Berechne:
a) Winkelgeschwindigkeit
b) Frequenz
c) Periodendauer
d) In der Position y=0,02m habe die Masse eine Geschwindigkeit von 1m/s. Welche
Amplitude hat die Schwingung?
2
40N
0,2m
11.) Eine Feder besitzt eine Federhärte von 100N/m. Wo befindet sich dann die Ruhelage,
wenn an die Feder eine Masse von 1kg gehängt wird? Dann wird die Feder mit der Masse
weitere 5cm nach unten gedehnt und losgelassen. Welche Position hat dann die Masse
bezogen auf die Ruhelage nach 5s?
Lösungen für die Schwingungsbeispiele
1.)=2,236/s. 2.)f2=0,707f1. 3.)y=−0,08m; k=9,87N/m; v=−0,18m/s. 4.)y=−0,042m;
v=1.11m/s. 5.)Start aus Ruhelage: F=0N; Start aus Umkehrpunkt: F=0,5N. 6.)f=1,15Hz;
x0=0,19m. 7.)y=3,16m; 8.)x0=0,09m; T=1,032s. 9.)a) y0=0,089m; b) y0=0,1095m.
10.)=14,14/s; f=2,25Hz; T=0,44s; y0=0,073m
11.)x0=0,1m; y(t=5s)=−0,048m;
Übungen Leifi-Physik
1.) Federpendelschwingung
http://www.leifiphysik.de/themenbereiche/mechanischeschwingungen/aufgaben#lightbox=/themenbereiche/mechanischeschwingungen/lb/mechanische-schwingungen-schwingung-federpendel
2.) Schwingung einer Wassersäule
http://www.leifiphysik.de/themenbereiche/mechanischeschwingungen/aufgaben#lightbox=/themenbereiche/mechanischeschwingungen/lb/mechanische-schwingungen-fluessigkeitspendel
3.) Schwingung eines Schwimmers
http://www.leifiphysik.de/themenbereiche/mechanischeschwingungen/aufgaben#lightbox=/themenbereiche/mechanischeschwingungen/lb/mechanische-schwingungen-schwimmer-der-angel
4.) Schwingung durch den Mittelpunkt der Erde: nur Fragestellungen a), b) und c)
http://www.leifiphysik.de/themenbereiche/mechanischeschwingungen/aufgaben#lightbox=/themenbereiche/mechanischeschwingungen/lb/mechanische-schwingungen-britischer-geologe
5.) Serienschaltung von Federpendeln
http://www.leifiphysik.de/themenbereiche/mechanischeschwingungen/aufgaben#lightbox=/themenbereiche/mechanischeschwingungen/lb/mechanische-schwingungen-serienschaltung-von-federpende-0
3