Gruppe „Verwandtschaftstreffen im Bienenstock“

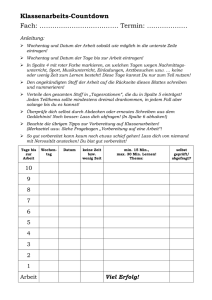
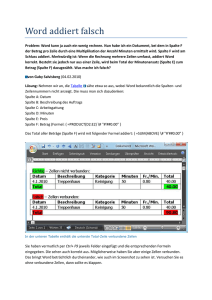
Gruppe „Verwandtschaftstreffen im Bienenstock“
1) Zeichnet euren persönlichen Stammbaum (bis zu den Ururgroßeltern)!
Hinweis: Wenn ihr manche Namen nicht kennt, so benutzt die Buchstaben
“V“ für Vater und “M“ für Mutter.
Die erste Vorfahrengeneration sind eure Eltern. Die Großeltern sind eure zweite
usw. Füllt nun folgende Tabelle aus:
k
Anzahl der Vorfahren in
Anzahl der Frauen in
Anzahl der Männer
(Vorfahrengeneration)
dieser Generation
dieser Generation
in dieser Generation
1
2
3
4
Schreibt man die Zahlen aus der blauen Spalte nacheinander auf, so könnte man
diese Auflistung als Folge (an) = (a1, a2, …) betrachten. Findet eine explizite
Darstellung dieser Folge:
ak = …………………………….
1
Das funktioniert auch für die anderen beiden Spalten. Bestimmt auch für diese
Folgen eine explizite Darstellung!

Rote Spalte (Anzahl der Frauen der k-ten Generation):
bk = ………………………….

Grüne Spalte (Anzahl der Männer der k-ten Generation):
ck = …………………………..
Findet nun auch die rekursiven Darstellungen der drei Folgen:

(an): ……………………………………………….

(bn): ……………………………………………….

(cn): ……………………………………………….
Bemerkung: Die drei Folgen sind unendlich, falls wir alle
Vorfahrengenerationen betrachten (stimmt das so?).
2) Nun wollen wir den Stammbaum einer Drohne (= männliche
Biene) untersuchen.
Im Biologieunterricht der dritten Klasse habt ihr gelernt, dass
sich Drohnen aus den unbefruchteten Eiern der Königin
entwickeln, weibliche Bienen aus den befruchteten.
Das bedeutet:

Eine Drohne hat eine Mutter, aber keinen Vater

Eine weibliche Biene hat Vater und Mutter
Zeichne nun mit diesem Wissen den Stammbaum einer Drohne bis zur sechsten
Vorfahrengeneration! Benutze dazu einen Bleistift und verwende folgende
Abkürzungen:
D… Drohne
B… weibliche Biene
2
Wie in Abschnitt 1) vervollständigt ihr folgende Tabelle:
Hinweis: Wir nehmen die „nullte Vorfahrengeneration“ dazu (das ist die
Drohne selbst)
k
Anzahl der Vorfahren
Anzahl der weiblichen
Anzahl der Drohnen
Vorfahrengeneration
in dieser Generation
Bienen in dieser Generation
in dieser Generation
0
1
2
3
4
5
6
Nun interpretieren wir die Elemente in einer Spalte wieder als Folge. Würde
man alle Vorfahrengenerationen anschreiben, so wäre sie unendlich (stimmt das
so?). Schreibt die Anfangsglieder für diese Folgen auf:
3

Violette Spalte (Gesamtzahl der Vorfahren in einer Generation):
(dn) = …………………………………………….

Orange Spalte (Anzahl der weiblichen Bienen der Generation):
(en) = …………………………………………….

Türkise Spalte (Anzahl der Drohnen der Generation):
(fn) = …………………………………………….
Beobachtet diese drei Folgen genau. Stehen sie in Verbindung? Wenn ja, wie?
……………………………………………………………………………………
……………………………………………………………………………………
………………………………………………………............................................
Versucht, ein Bildungsgesetz für die Folge (dn) anzugeben (in Worten, dann
entweder explizit oder rekursiv)!
……………………………………………………………………………………
……………………………………………………………………………………
Der italienische Mathematiker Leonardo da Pisa, auch „Fibonacci“ genannt, entwickelte zu
Beginn des 13. Jahrhunderts die unendliche Folge
f n  (1,1,2,3,5,8,13,21,34,55,89,...).
Diese wird zu seinen Ehren „Fibonacci-Folge“ genannt. Sie hat folgende
rekursive Darstellung:
f 0  1, f1  1, f n  f n2  f n1 n  2
Ein Glied der Folge ist also für n ≥ 2 die Summe seiner beiden Vorgänger.
Fibonacci hat mit dieser Folge die Vermehrung von Kaninchen beschrieben. Sie taucht aber
auch in vielen anderen Kontexten auf, zum Beispiel im Stammbaum einer Drohne.
4