Deduktive Datenbanken

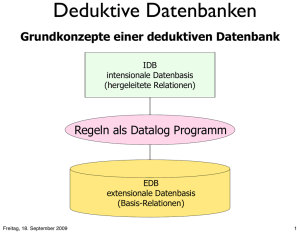
Deduktive Datenbanken
Grundkonzepte einer deduktiven Datenbank
IDB
intensionale Datenbasis
(hergeleitete Relationen)
Regeln als Datalog Programm
EDB
extensionale Datenbasis
(Basis-Relationen)
Donnerstag, 12. November 2009
1
Die relationale Uni-DB
PersNr
2125
2126
2127
2133
2134
2136
2137
Professoren
Name
Rang
Sokrates
C4
Russel
C4
Kopernikus
C3
Popper
C3
Augustinus
C3
Curie
C4
Kant
C4
hören
MatrNr
26120
27550
27550
28106
28106
28106
28106
29120
29120
29120
29555
25403
VorlNr
5001
5001
4052
5041
5052
5216
5259
5001
5041
5049
5022
5022
Donnerstag, 12. November 2009
Raum
226
232
310
52
309
36
7
MatrNr
24002
25403
26120
26830
27550
28106
29120
29555
voraussetzen
Vorgänger Nachfolger
5001
5041
5001
5043
5001
5049
5041
5216
5043
5052
5041
5052
5052
5259
MatrNr
28106
25403
27550
prüfen
VorlNr PersNr Note
5001
2126
1
5041
2125
2
4630
2137
2
Studenten
Name
Xenokrates
Jonas
Fichte
Aristoxenos
Schopenhauer
Carnap
Theophrastos
Feuerbach
Semester
18
12
10
8
6
3
2
2
Vorlesungen
VorlNr
Titel
5001
Grundzüge
5041
Ethik
5043
Erkenntnistheorie
5049
Mäeutik
4052
Logik
5052 Wissenschaftstheorie
5216
Bioethik
5259
Der Wiener Kreis
5022 Glaube und Wissen
4630
Die 3 Kritiken
SWS
4
4
3
2
4
3
2
2
2
4
gelesen
von
2137
2125
2126
2125
2125
2126
2126
2133
2134
2137
2
Rekursion
•
•
Find alle Voraussetzungen von “Der Wiener Kreis”
Auch indirekte Voraussetzungen beliebiger Tiefe
select Vorgänger
???
from voraussetzen,Vorlesungen
???
where Nachfolger= VorlNr and
Donnerstag, 12. November 2009
Titel= `Der Wiener Kreis´
3
Voraussetzungsgraph
Der Wiener Kreis
5259
Wissenschaftstheorie
5052
Bioethik
5216
Erkenntnistheorie
5043
Ethik
5041
Mäeutik
5049
Grundzüge
5001
Donnerstag, 12. November 2009
4
Tiefe 2
select v1.Vorgänger
from voraussetzen v1, voraussetzen v2,Vorlesungen v
where v1.Nachfolger= v2.Vorgänger and
v2.Nachfolger= v.VorlNr and
v.Titel=`Der Wiener Kreis´
Donnerstag, 12. November 2009
5
Voraussetzungsgraph
Der Wiener Kreis
5259
Wissenschaftstheorie
5052
Bioethik
5216
Erkenntnistheorie
5043
Ethik
5041
Mäeutik
5049
Grundzüge
5001
Donnerstag, 12. November 2009
6
Tiefe n
select v1.Vorgänger
from voraussetzen v1
...
voraussetzen vn_minus_1
voraussetzen vn,
Vorlesungen v
where v1.Nachfolger= v2.Vorgänger and
...
vn_minus_1.Nachfolger= vn.Vorgänger and
vn.Nachfolger = v.VorlNr and
v.Titel= `Der Wiener Kreis´
Donnerstag, 12. November 2009
7
Voraussetzungsgraph
Der Wiener Kreis
5259
Wissenschaftstheorie
5052
Bioethik
5216
Erkenntnistheorie
5043
Ethik
5041
Mäeutik
5049
Grundzüge
5001
Donnerstag, 12. November 2009
8
Transitive Hülle
Der Wiener Kreis
5259
Wissenschaftstheorie
5052
Bioethik
5216
Erkenntnistheorie
5043
Ethik
5041
Mäeutik
5049
Grundzüge
5001
Donnerstag, 12. November 2009
9
Rekursive Anfragen
with recursive TransVorl (Vorg, Nachf)
as (select Vorgänger, Nachfolger from voraussetzen
union all
select t.Vorg, v.Nachfolger
from TransVorl t, voraussetzen v
where t.Nachf= v.Vorgänger)
select Titel from Vorlesungen where VorlNr in
(select Vorg from TransVorl where Nachf in
(select VorlNr from Vorlesungen
where Titel= `Der Wiener Kreis´) )
Donnerstag, 12. November 2009
10
Rekursion in SQL
•
•
Man kann with rekursiv verwenden
•
Die Definition der Sicht wird so lange iterativ neu
berechnet, bis keine neuen Tupel hinzukommen
(Fixpunkt)
•
Vorsicht: Anfrage terminiert evtl. nicht! (Wann?)
Mehrere Teilklauseln können mit union (all)
verbunden werden
Donnerstag, 12. November 2009
11
Datalog
•
•
Anfragesprache, basierend auf Prädikatenlogik
Ursprung in der Logikprogrammierung
•
•
•
•
•
“Prolog ohne Funktionen”
Relationales Datenmodell, erweitert um Regeln
Einfachere Syntax als SQL
Rekursive Anfragen leicht zu formulieren
Nützlich für formale Untersuchungen von
Anfrageeigenschaften
Donnerstag, 12. November 2009
12
Datalog
Regel:
sokLV(T,S) :-vorlesungen(V,T,S,P ), professoren(P, „Sokrates“,R,Z ), >(S,2).
Grundbausteine der Regeln sind atomare Formeln oder Literale:
q(A1, ..., Am).
q ist dabei der Name einer Basisrelation, einer abgeleiteten Relation oder eines
eingebauten Prädikats: <,=,>,…
Beispiel: professoren(S, „Sokrates“,R,Z ).
Äquivalenter Domänenkalkül-Ausdruck:
{[t,s] | ∃v,p ([v,t,s,p] ∈ Vorlesungen ∧
∃n,r,z ([p,n,r,z] ∈ Professoren ∧
n = „Sokrates“ ∧ s > 2))}
Donnerstag, 12. November 2009
13
Datalog-Regel
•
Linke Seite ist der Kopf (Head, Goal) der Regel,
rechte Seite Rumpf (Body)
•
Jedes qj (...) ist eine atomare Formel. Die Prädikate qj
werden auch als Subgoals bezeichnet.
•
X1, ...,Xm sind Variablen, die mindestens einmal auch im
Rumpf vorkommen müssen
•
Aij sind Konstanten oder Variablen
Donnerstag, 12. November 2009
14
Datalog-Regel
•
•
:- entspricht Implikation, Rumpf
Kopf
Logisch äquivalente Form obiger Regel:
p(...) ∨ ¬q1 (...) ∨... ∨ ¬qn (...)
Donnerstag, 12. November 2009
15
Beispiel Datalog-Programm
•
•
Voraussetzen: {[Vorgänger, Nachfolger]}
Vorlesungen: {VorlNr, Titel, SWS, gelesenVon]}
geschwisterVorl(N 1, N 2) :- voraussetzen(V, N1),voraussetzen(V, N2)), N1 < N2.
geschwisterThemen(T 1, T 2) :- geschwisterVorl(N1, N2),
vorlesungen(N1, T1, S1, R1),
vorlesungen(N2, T2, S2, R2).
aufbauen(V,N ) :- voraussetzen(V,N )
aufbauen(V,N ) :- aufbauen(V,M ), voraussetzen(M,N ).
verwandt(N,M ) :- aufbauen(N,M ).
verwandt(N,M ) :- aufbauen(M,N ).
verwandt(N,M ) :- aufbauen(V,N ), aufbauen(V,M ).
Donnerstag, 12. November 2009
16
Analogie zur EDB/IDB in rel. DBMS
• Basis-Relationen entsprechen den EDB.
• Sichten entsprechen den IDB:
•
„Aufbauen“ als Regeln in einem deduktiven DBMS:
aufbauen(V,N ) :- voraussetzen(V,N )
aufbauen(V,N ) :- aufbauen(V,M ), voraussetzen(M,N ).
•
„Aufbauen“ als Sichtdefinition in DB2:
create view aufbauen(V,N) as
(select Vorgaenger, Nachfolger
from voraussetzen
union all
select a.V, v.Nachfolger
from aufbauen a, voraussetzen v
where a.N = v.Vorgaenger)
select * from aufbauen
Donnerstag, 12. November 2009
17
Abhängigkeitsgraph
geschwisterThema
verwandt
geschwisterVorl
vorlesungen
aufbauen
voraussetzen
Donnerstag, 12. November 2009
18
Rekursion
•
Abhängigkeitsgraph enthält Zykel
•
•
Programm ist rekursiv
Im Beispiel: aufbauen
Donnerstag, 12. November 2009
19
Sicherheit von Datalog-Regeln
•
Es gibt unsichere Regeln, wie z.B.
ungleich(X,Y) :- X ≠ Y.
Diese definieren unendliche Relationen.
•
Datalog-Regel ist sicher, wenn alle Variablen im Kopf
beschränkt (range restricted) sind
•
Variable X ist range-restricted, wenn im Rumpf
•
•
•
X in einem normalen (nicht eingebauten) Prädikat vorkommt
Prädikat der Form X = c mit einer Konstante c vorkommt
Prädikat X = Y vorkommt, und Y ist range-restricted
Donnerstag, 12. November 2009
20
Auswertung nicht-rekursiver
Datalog-Programme
•
Materialisierung der IDB-Prädikate
•
•
•
Umwandlung der Regeln in relationale Algebra
Materialisierung erfolgt in topologischer Reihenfolge
Materialisierte IDB-Prädikate können wie EDBPrädikate behandelt werden
Donnerstag, 12. November 2009
21
Ein nicht rekursives Programm
geschwisterVorl(N 1, N 2) :- voraussetzen(V, N1),voraussetzen(V, N2)), N1 < N2.
geschwisterThemen(T 1, T 2) :- geschwisterVorl(N1, N2),
vorlesungen(N1, T1, S1, R1),
vorlesungen(N2, T2, S2, R2).
voraussetzen
geschwisterThema
geschwisterVorl
vorlesungen
Mögl. Topologische Ordnung:
voraussetzen, geschwisterVorl, vorlesungen, geschwisterThema
Donnerstag, 12. November 2009
22
Auswertung nicht-rekursiver
Datalog-Programme: Übersicht
Schritt 1:
Für jede Regel mit dem Kopf p(...), also
p(...) :- q1(...), ..., qn(...).
bilde eine Relation mit allen im Körper der Regel vorkommenden
Variablen als Attribute (Join der materialisierten Relationen für qi sowie
Selektion mit restlichen Prädikaten)
Wichtig: Korrekte Umbenennung von Variablen
Schritt 2:
Projiziere alle Relationen aus Schritt I auf die Variablen, die im Kopf
vorkommen, und bilde für jedes Prädikat die Vereinigung dieser
Relationen.
Donnerstag, 12. November 2009
23
Auswertung von Geschwister Vorlesungen
und Geschwister Themen
•
Die Relation zu Prädikat gV ergibt sich nach Schritt 1zu
σN1<N2 (Vs1(V, N1) A Vs2(V, N2))
Vs1(V, N1) := ρV←$1(ρN1 ←$2 (Voraussetzen))
Vs2(V, N1) := ρV←$1(ρN2 ←$2 (Voraussetzen))
•
Gemäß Schritt 2. ergibt sich:
GV(N1, N2) := ΠN1, N2 (σN1<N2(Vs1(V, N1) A Vs2(V, N2)))
•
Analog ergibt sich für die Herleitung von GT:
GT(T1,T2) := ΠT1,T2(GV(N1,N2) A VL1(N1,T1,S1,R1) A VL2(N2,T2,S2,R2))
Donnerstag, 12. November 2009
24
Ausprägung der Relationen GeschwisterVorl
und GeschwisterThemen
GeschwisterVorl
GeschwisterThemen
N1
N2
5041
5043
T1
T2
5043
5049
Ethik
Erkenntnistheorie
5041
5049
Erkenntnistheorie
Mäeutik
5052
5216
Ethik
Mäeutik
Wissenschaftstheorie
Bioethik
Donnerstag, 12. November 2009
25
Auswertungs-Algorithmus:
Details
Dabei sind die Vi die in qi(…) vorkommenden Variablen.
Das Selektionsprädikat Fi setzt sich aus einer Menge konjunktiv
verknüpfter Bedingungen zusammen.
Donnerstag, 12. November 2009
26
Selektionsprädikat Fi
•
Konstante c an j-ter Stelle qi(...,c,...)
$j = c
•
Mehrfach verwendete Variable X in qi(...,X,...,X,...)
(Positionen k und l)
$k = $l
Donnerstag, 12. November 2009
27
Umbenennung
•
Die Attribute der Relation werden entsprechend
der Variablennamen im Subgoal benannt
qi(...,V1,...,Vn,...)
k1
kn
Donnerstag, 12. November 2009
ΠV1,...,Vn(ρV1←$k1,...,Vn←$kn(Ei))
28
Auswertungs-Algorithmus
Für Variable Y, die nicht in den normalen Prädikaten
vorkommt, gibt es zwei Möglichkeiten:

Sie kommt nur als Prädikat
Y=c
für eine Konstante c vor. Dann bilde einstellige Relation
DY := ρY←$1 ({[c]})

Sie kommt als Prädikat X = Y vor, und X kommt in
Prädikat qi(…,X,…) an k—ter Stelle vor. Dann bilde Relation
DY := ρY←$k (Π$k (Qi)) .
Donnerstag, 12. November 2009
29
Auswertungs-Algorithmus:
Details
Bilde Join aus den Ei und DY
E := E1 A ... A En A DY A...
und wende Selektion
σF (E)
an. F ist konjunktiven Verknüpfung der Vergleichsprädikate
X ФY
Projiziere auf die im Kopf der Regel vorkommenden Variablen:
ΠX
1,…, Xm
Donnerstag, 12. November 2009
(σF (E ))
30
Beispiel: nahe verwandte Vorlesungen
(r1) nvV(N1,N2) :- gV(N1,N2).
(r2) nvV(N1,N2) :- gV(M1,M2),vs(M1,N1),vs(M2,N2).
Für die erste Regel erhält man
Für die zweite Regel
Daraus ergibt sich dann durch die Vereinigung
Donnerstag, 12. November 2009
31
Vereinigung
•
Die Ausdrücke für alle Regeln eines Prädikats werden
vereinigt, um die Ergebnisrelation zu erhalten
•
Vereinigung und evtl. andere Regeln erfordern
einheitliches Schema
•
•
Also noch Umbenennung erforderlich
Sonderfall:Variablen, die im Kopf mehrfach vorkommen
•
Durch neue Variablen und Gleichheitsprädikate ersetzen
Donnerstag, 12. November 2009
32
Auswertung rekursiver Regeln
Aufbauen
V
N
5001
5041
5001
5043
5001
5049
a(V,N) :- vs(V,N).
5041
5216
5041
5052
a(V,N) :- a(V,M),vs(M,N).
5043
5052
5052
5259
5001
5216
5001
5052
5001
5259
5041
5259
5043
5259
Donnerstag, 12. November 2009
33
Auswertung rekursiver Regeln
Betrachten wir das Tupel [5001, 5052] aus der Relation
Aufbauen. Dieses Tupel kann wie folgt hergeleitet
werden:
1. a (5001, 5043) folgt aus der ersten Regel, da
vs (5001, 5043) gilt.
2. a (5001, 5052) folgt aus der zweiten Regel, da
a)
a (5001, 5043) nach Schritt 1. gilt und
b)
vs (5043, 5052) gemäß der EDB-Relation Voraussetzen gilt.
Donnerstag, 12. November 2009
34
Naive Auswertung durch Iteration
A := {}: /*Initialisierung auf die leere Menge */
repeat
A’:=A;
/* Erste Regel */
A:=Vs(V,N)
/* Zweite Regel */
A:=A∪ΠV,N(ρ$1→V,$2→M(A’)A ρ$1→M,$2→N(Vs)
until A‘ = A
output A;
Donnerstag, 12. November 2009
35
Naive Auswertung durch Iteration
1. Erster Durchlauf kopiert Voraussetzen nach A
2. Im zweiten Schritt kommen die Tupel [5001,5216],
[5001,5052], [5041,5259] und [5043,5259] hinzu.
3. Neues Tupel [5001,5259]
4. Abbruchbedingung A‘ = A erfüllt
Donnerstag, 12. November 2009
36
(Naive) Auswertung der rekursiven Regel aufbauen
Schritt
A
1
[5001,5041], [5001,5043], [5001,5049],
[5041,5216], [5041,5052], [5043,5052],
[5052,5259]
2
[5001,5041], [5001,5043], [5001,5049],
[5041,5216], [5041,5052], [5043,5052],
[5052,5259]
[5001,5216], [5001,5052], [5041,5259],
[5043,5259],
3
[5001,5041], [5001,5043], [5001,5049],
[5041,5216], [5041,5052], [5043,5052],
[5052,5259]
[5001,5216], [5001,5052], [5041,5259],
[5043,5259], [5001,5259]
4
wie in Schritt 3 (keine Veränderung, also
Terminierung des Algorithmus
Donnerstag, 12. November 2009
37
Inkrementelle (semi-naive)
Auswertung rekursiver Regeln
Beobachtung: Für die Generierung eines neuen Tupels t der rekursiv definierten IDBRelation P ist eine bestimmte Regel
p(...) :- q1(...), ..., qn(...).
„verantwortlich“ ist. Es wird in der iterativen Auswertung also ein Ausdruck der Art
E(Q1AQ2A…AQn)
iterativ ausgewertet. Es reicht aber aus
E(ΔQ1 A Q2 A…A Qn )∪ E(Q1 A ΔQ2 A…A Qn )∪ …∪
E(Q1 A Q2 A…A Δ Qn )
auszuwerten.
Donnerstag, 12. November 2009
38
Beispiel
Dieses Tupel wurde aus dem folgenden Join gebildet:
[
]A [ 5052 , 5259 ]
5001
,
5052
1 42 43
1 4 2 4 3
t1 ∈ A
Donnerstag, 12. November 2009
t 2 ∈ Vs
39
semi-naive Auswertung
ΔA := Vs(V,N) /* 1. Regel */
ΔA := ΔA ∪ ∏V,N( A(V,M) A Vs(M,N)) /* 2. Regel */
ΔVs =∅
A:= ΔA
repeat
ΔA’:= ΔA;
ΔA := Vs(V,N) /* 1. Regel */
ΔA := ΔA ∪ ∏V,N( A(V,M) AΔVs(M,N))
/* 2. Regel */
∪ ∏V,N(ΔA’(V,M) A Vs(M,N))
ΔA := ΔA - A
A := A ∪ ΔA
until ΔA=∅
Donnerstag, 12. November 2009
40
Illustration der semi-naiven
Auswertung von Aufbauen
Schritt
ΔA
Initialisierung
(Zeile 2. und 3.)
(sieben Tupel aus VS)
[5001,5042], [5001,5043] [5043,5052],
[5041,5052] [5001,5049], [5001,5216]
[5052,5259]
1. Iteration
(Pfade der Länge 2)
[5001,5216], [5001,5052] [5041,5259],
[5043,5259]
2. Iteration
(Pfade der Länge 3)
[5001,5259]
3. Iteration
∅
(Terminierung)
Donnerstag, 12. November 2009
41
Bottom-Up oder Top-Down
Auswertung
(r1) a (V,N) :- vs (V,N).
(r2) a (V,N) :-a (V,M),vs(M,N).
query (V ) :- A(V,5052).
Donnerstag, 12. November 2009
42
Rule/Goal-Baum zur Top-Down
Auswertung
a(V,5052)
r1 : a(V,5052) :- vs(V,5052)
vs(V,5052)
r1 : a(V,M1) :- vs(V,M1)
vs(V,M1)
Donnerstag, 12. November 2009
r2 : a(V,5052) :- a(V,M1),vs(M1,5052)
a(V,M1)
vs(M1,5052)
r2 : a(V,M1) :- a(V,M2),v2(M2,M1)
a(V,M2)
:
vs(M2,M1)
43
Rule/Goal-Baum mit Auswertung
a(V,5052)
r1 : a(V,5052) :- vs(V,5052)
vs(V,5052)
r2 : a(V,5052) :- a(V,M1),vs(M1,5052)
a(V,M1)
V ∈ {5041,5043}
r1 : a(V,M1) :- vs(V,M1)
vs(V,M1)
V ∈ {5001}
Donnerstag, 12. November 2009
vs(M1,5052)
M1 ∈ {5041,5043}
r2 : a(V,M1) :- a(V,M2),v2(M2,M1)
a(V,M2)
:
V∈ Ø
vs(M2,M1)
M2 ∈ {5001}
44
Negation im Regelrumpf
indirektAufbauen(V,N) :- aufbauen(V,N), ¬voraussetzen(V,N)
Stratifizierte Datalog-Programme
Programm heisst stratifiziert, wenn bei allen Regeln mit
negiertem Subgoal
p (...) :- q1 (...), ..., ¬qi (...), ..., qn (...).
gilt: Es gibt keine Pfade im Abhängigkeitsgraph von qi nach p.
Donnerstag, 12. November 2009
45
Auswertung von Regeln mit
Negation
Donnerstag, 12. November 2009
46
Ein etwas komplexeres Beispiel
Donnerstag, 12. November 2009
47
Ausdruckskraft von Datalog
•
Datalog, eingeschränkt auf nicht-rekursive
Programme mit Negation, wird auch als
Datalog ¬non-rec bezeichnet
•
Datalog¬ non-rec hat genau die gleiche
Ausdruckskraft wie die relationale Algebra
Donnerstag, 12. November 2009
48
Datalog-Formulierung der
relationalen Algebra-Operatoren
Selektion
Projektion
Join
Π
Titel , Name
(Vorlesunge nA
gelesenVon= PersNr
Professore n )
query (T , N ): −vorlesungen (V , T , S , R ), professore n (R , N , Rg , Ra ).
Donnerstag, 12. November 2009
49
Datalog-Formulierung der
relationalen Algebra-Operatoren
Kreuzprodukt
Vereinigung
(
)
(
)
∪Π
Assistente
n
Professore
n
PersNr Name
PersNr,Name
Π
,
query( PersNr , Name) : −assistenten( PersNr , Name, F , B ).
query( PersNr , Name) : − professoren( PersNr , Name, Rg , Ra ).
Donnerstag, 12. November 2009
50
Datalog-Formulierung der
relationalen Algebra-Operatoren
Mengendifferenz
Donnerstag, 12. November 2009
51