(V, N) :

Deduktive Datenbanken
 Deduktive Datenbanken schlagen eine Brücke zwischen
relationalen Datenbanken und den logik-basierten
Programmiersprachen (hier: Prolog).
Die persistent gespeicherten Relationen einer Datenbanken
werden hier als Prädikate der Logik erster Stufe angesehen:
Genau falls sich ein Tupel (x,y,z) in Relation R befindet, wird
das zugehörige Prädikat r(x,y,z) mit true bewertet.
Damit entsprechen die persistenten Relationen der
Datenbank der Faktenbasis in Prolog.
Eine Regelsprache, Datalog (Data & Logic), wird
verwendet, um aus diesen vorhandenen Fakten, neues
"Wissen" abzuleiten (zu deduzieren).
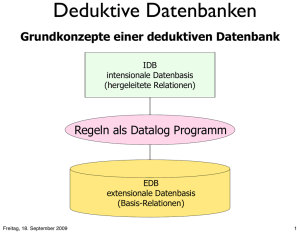
Deduktive Datenbanken
Grundkonzepte einer deduktiven Datenbank
IDB
intensionale Datenbasis
(hergeleitete Relationen)
Regeln als Datalog Programm
EDB
extensionale Datenbasis
(Basis-Relationen)
Deduktive Datenbanken:
Terminologie
 Die extensionale Datenbasis (EDB), die manchmal auch
Faktenbasis genannt wird. Die EDB besteht aus einer Menge
von Relationen(Ausprägungen) und entspricht einer „ganz
normalen“ relationalen Datenbasis.
 Die Deduktionskomponente, die aus einer Menge von
(Herleitungs-)Regeln besteht. Die Regelsprache heißt Datalog.
 Die intensionale Datenbasis (IDB), die aus einer Menge von
hergeleiteten Relationen(Ausprägungen) besteht. Die IDB wird
durch Auswertung des Datalog-Programms aus der EDB
generiert.
Beispiel: Rekursion in
Prolog/Datalog
5
1
2
3
4
6
 Faktenbasis zu diesem gerichteten Graphen:
kante(1,2).
kante(2,3).
kante(3,4).
kante(4,5).
kante(4,6).
kante(6,7).
kante(3,6).
7
Beispiel: Rekursion in
Prolog/Datalog
5
1
2
3
4
6
7
 Leite aus der Faktenbasis die Pfade in diesem gerichteten
Graphen ab:
kante(1,2).
kante(2,3).
kante(3,4).
kante(4,5).
kante(4,6).
kante(6,7).
kante(3,6).
pfad(V,N) :- kante(V,N).
pfad(V,N) :- kante(V,Z), pfad(Z,N).
Alternative Notation:
pfad(V,N)  kante(V,N).
 pfad(V,N)  kante(V,Z)  pfad(Z,N).
Rekursion in SQL(?)
 Bestimme die Voraussetzungen für die Vorlesung "Der Wiener
Kreis":
SELECT Vorgänger
FROM voraussetzen, Vorlesungen
WHERE VorlNr = Nachfolger
AND
Titel = "Der Wiener Kreis"
voraussetzen
Vorgänger Nachfolger
Vorlesungen
VorlNr
Titel
SWS gelesen
Von
5001
Grundzüge
4
2137
5041
Ethik
4
2125
5043
Erkenntnistheorie
3
2126
5001
5041
5049
Mäeutik
2
2125
5001
5043
4052
Logik
4
2125
5001
5049
5052 Wissenschaftstheorie
3
2126
5041
5216
5216
Bioethik
2
2126
5043
5052
5259
Der Wiener Kreis
2
2133
5041
5052
5022
Glaube und Wissen
2
2134
5052
5259
4630
Die 3 Kritiken
4
2137
Der Wiener Kreis
5259
Wissenschaftstheorie
5052
Erkenntnistheorie
5043
Bioethik
5216
Ethik
5041
Grundzüge
5001
Mäeutik
5049
Rekursion in SQL(?): Pfade der Länge 2
SELECT v1.Vorgänger
FROM
voraussetzen v1, voraussetzen v2, Vorlesungen v
WHERE v1.Nachfolger = v2.Vorgänger AND
v2.Nachfolger = v.VorlNr AND
v.Titel = "Der Wiener Kreis"
voraussetzen
voraussetzen
Vorgänger Nachfolger
Vorgänger Nachfolger
5001
5041
5001
5041
5001
5043
5001
5043
5001
5049
5001
5049
5041
5216
5041
5216
5043
5052
5043
5052
5041
5052
5041
5052
5052
5259
5052
5259
Vorlesungen
VorlNr
Titel
SWS gelesen
Von
5001
Grundzüge
4
2137
5041
Ethik
4
2125
5043
Erkenntnistheorie
3
2126
5049
Mäeutik
2
2125
4052
Logik
4
2125
5052 Wissenschaftstheorie
3
2126
5216
Bioethik
2
2126
5259
Der Wiener Kreis
2
2133
5022
Glaube und Wissen
2
2134
4630
Die 3 Kritiken
4
2137
Rekursion in SQL(?): Pfade der Länge n
SELECT
FROM
WHERE
v1.Vorgänger
voraussetzen v1

voraussetzen vn-1
voraussetzen vn,
Vorlesungen v
v1.Nachfolger= v2.Vorgänger and

vn-1.Nachfolger= vn.Vorgänger and
vn.Nachfolger = v.VorlNr and
v.Titel = "Der Wiener Kreis"
n-facher self join der Relation voraussetzen
Transitive Hülle der Relation R(A,B)
transA,B(R) = { (a,b)  k  IN (t1, ..., tk  R (
t1.A = t2.B


tk-1.A = tk.B

t1.A = a

tk.B = b))
}
Der Wiener Kreis
Wissenschaftstheorie
Erkenntnistheorie
Bioethik
Ethik
Grundzüge
Extensional
Intensional
Mäeutik
Rekursion(!) in DB2/SQL:1999: Alle
Voraussetzungen für "Der Wiener Kreis"
WITH TransVorl (Vorg, Nachf) AS (
SELECT Vorgänger, Nachfolger FROM voraussetzen
UNION ALL
Rekursion!
SELECT t.Vorg, v.Nachfolger
FROM TransVorl t, voraussetzen v
WHERE t.Nachf= v.Vorgänger)
Abbruch? Sobald View stabil.
SELECT Titel FROM Vorlesungen WHERE VorlNr IN
(SELECT Vorg FROM TransVorl WHERE Nachf in
(SELECT VorlNr FROM Vorlesungen
WHERE Titel = "Der Wiener Kreis") )
Datalog: Regeln, Literale
Regel:
sokLV(T,S) :- vorlesungen(V,T,S,P ), professoren(P, "Sokrates",R,Z ), >(S,2).
Äquivalenter Domänenkalkül-Ausdruck:
{ [t,s] | v,p ([v,t,s,p] Vorlesungen 
n,r,z ([p,n,r,z]  Professoren 
n = "Sokrates"  s > 2))}
Grundbausteine der Regeln sind atomare Formeln (oder Literale):
q(A1, ..., Am).
q ist dabei der Name einer Basisrelation, einer abgeleiteten Relation oder eines
eingebauten Prädikats: <,=,>,…
Beispiel: professoren(S, "Sokrates",R,Z ).
Datalog: Regeln
p( X 1 ,..., X m ) : - q1 ( A11,..., A1m1 ),..., qn ( An1 ,..., Anmn ).
 Jedes qj (...) ist eine atomare Formel. Die qj werden oft als
Subgoals bezeichnet.
 X1, ...,Xm sind Variablen, die mindestens einmal auch auf der
rechten Seite des Zeichens :- vorkommen müssen.
 Logisch äquivalente Form obiger Regel (Hornklausel):
p(...)  ¬q1 (...) … ...  ¬qn (...)
 Wir halten uns an folgende Notation:
Prädikate beginnen mit einem Kleinbuchstaben.
Die zugehörigen Relationen – seien es EDB- oder IDBRelationen – werden mit gleichem Namen, aber mit einem
Großbuchstaben beginnend, bezeichnet.
Beispiel: Datalog-Programm
 Zur Bestimmung von (thematisch) verwandten Vorlesungspaaren
 EDB-Relationen: Voraussetzen: {[Vorgänger, Nachfolger]}
Vorlesungen: {VorlNr, Titel, SWS, gelesenVon]}
geschwisterVorl(N1, N2) :- voraussetzen(V, N1),
voraussetzen(V, N2)), N1 < N2.
geschwisterThemen(T1, T2) :- geschwisterVorl(N1, N2),
vorlesungen(N1, T1, S1, R1),
vorlesungen(N2, T2, S2, R2).
aufbauen(V,N ) :- voraussetzen(V,N )
aufbauen(V,N ) :- aufbauen(V,M ), voraussetzen(M,N ).
verwandt(N,M ) :- aufbauen(N,M ).
verwandt(N,M ) :- aufbauen(M,N ).
verwandt(N,M ) :- aufbauen(V,N ), aufbauen(V,M ).
Analogie zur EDB/IDB in RDBMS
 Basis-Relationen entsprechen den EDB.
 Sichten entsprechen den IDB:
"aufbauen" als Regeln in einem deduktiven DBMS:
aufbauen(V,N ) :- voraussetzen(V,N )
aufbauen(V,N ) :- aufbauen(V,M ), voraussetzen(M,N ).
"aufbauen" als Sichtdefinition in DB2:
CREATE VIEW aufbauen(V,N) as
(SELECT Vorgaenger, Nachfolger
FROM
voraussetzen
UNION ALL
SELECT a.V, v.Nachfolger
FROM aufbauen a, voraussetzen v
WHERE a.N = v.Vorgaenger);
SELECT * FROM aufbauen;
Eigenschaften von Datalog-Programmen
Regel-Abhängigkeitsgraph (
verwandt
aufbauen
voraussetzen
= "wird verwendet von")
geschwisterThemen
geschwisterVorl
vorlesungen
 Ein Datalog-Programm ist rekursiv, wenn der
Abhängigkeitsgraph einen (oder mehrere) Zyklen hat
 Unser Beispielprogramm ist rekursiv: aufbauen  aufbauen
Sicherheit von Datalog-Regeln
 Es gibt unsichere Regeln, wie z.B.
ungleich(X, Y) :- X ≠ Y.
Diese definieren unendliche Relationen.
 Eine Datalog-Regel ist sicher, wenn alle Variablen im Kopf
eingeschränkt (range restricted) sind. Dies ist für eine
Variable X dann der Fall, wenn:
die Variable im Rumpf der Regel in mindestens einem
normalen Prädikat – also nicht nur in eingebauten
Vergleichsprädikaten – vorkommt oder
ein Prädikat der Form X = c mit einer Konstante c im Rumpf
der Regel existiert oder
ein Prädikat der Form X = Y im Rumpf vorkommt, und
nachgewiesen ist, dass Y eingeschränkt ist.
Ein zyklenfreier Abhängigkeitsgraph
 gV(N1, N2) :- vs(V, N1), vs(V, N2), N1 < N2.
 gT(T1, T2) :- gV(N1, N2), vL(N1, T1, S1, R1), vL(N2, T2, S2, R2)
gT
gV
vs
vL
 Eine mögliche topologische Sortierung ist: vs, gV, vL, gT.
 Auswertungsreihenfolge für Prädikate!
Auswertung nicht-rekursiver
Datalog-Programme
1.
Für jede Regel mit dem Kopf p(...) , also
p(...) :- q1(...), ..., qn(...).
bilde eine Relation, in der alle im Körper der Regel vorkommenden
Variablen als Attribute vorkommen. Diese Relation wird im
wesentlichen durch einen natürlichen Verbund der Relationen Q1,
..., Qn, die den Relationen der Prädikate q1, ..., qn entsprechen, gebildet.
Man beachte, dass diese Relationen Q1, ..., Qn wegen der Einhaltung
der topologischen Sortierung bereits ausgewertet (materialisiert) sind.
2.
Da das Prädikat p durch mehrere Regeln definiert sein kann, werden
die Relationen aus Schritt 1 vereinigt. Hierzu muss man vorher auf die
im Kopf der Regeln vorkommenden Attribute projizieren. Wir
nehmen an, dass alle Köpfe der Regeln für p dieselben Attributnamen
an derselben Stelle verwenden – durch Umformung der Regeln kann
man dies immer erreichen.
Auswertung von Geschwister
Vorlesungen und Geschwister Themen
 Die Relation zu Prädikat gV ergibt sich nach Schritt 1 aus folg.
Relationenalgebraausdruck:
 N1<N2 (Vs1(V, N1)
Vs2(V, N2))
Vs1(V, N1) := V$1(N1 $2 (Vs1(Voraussetzen)))
 Die dadurch definierte Relation enthält Tupel [v, n1, n2] mit:
 Das Tupel [v, n1] ist in der Relation Voraussetzen enthalten,
 das Tupel [v, n2] ist in der Relation Voraussetzen enthalten und
 n1 < n2.
 Gemäß Schritt 2. ergibt sich:
GV(N1, N2) := N1, N2 ( N1<N2 (Vs1(V, N1)
Vs2(V, N2)))
 Analog ergibt sich für die Herleitung von GT:
GT(T1,T2) := T1,T2(GV(N1,N2)
VL1(N1,T1,S1,R1)
VL2(N2,T2,S2,R2))
Veranschaulichung der EDB-Relation
Voraussetzen
5259 (WienerKreis)
5216 (Bioethik)
5052 (Wiss. Theorie)
5041 (Ethik)
5043 (Erk. Theorie)
5001 (Grundzüge)
5049 (Mäeutik)
Ausprägung der Relationen GeschwisterVorl
und GeschwisterThemen
GeschwisterVorl
GeschwisterThemen
N1
N2
T1
T2
5041
5043
5041
5052
5043
5049
5049
5216
Ethik
Erkenntnistheorie
Erkenntnistheorie
Mäeutik
Ethik
Wissenschaftstheorie
Mäeutik
Bioethik
Auswertung nicht-rekursiver
Datalog-Regeln
 Ziel: Auswertung der Datalog-Regel
p(X1,…,Xm) :- q1(A11,…,A1m1), …, qn(An1,…,Anmn).
 Topologische Sortierung: Prädikate qi seien schon zu Relationen
Qi ausgewertet. Schema: Qi: { [ $1,…,$mi ] }.
 Für jedes der Subgoals qi(Ai1,…,Aimi) bilde den folgenden
Ausdruck der Relationenalgebra:
Ei :=  … Vi $i … ( Pi (  Fi (Qi)))
 Die Pi sind die in qi(…) auftretenden Variablenpositionen, Vi ist
der im Subgoal an Position i benutzte Variablenname ($i  Pi)
und Fi ist eine konjunktive Selektionsbedingung, die wie folgt
gebildet wird (s. nächste Folien).
Auswertung nicht-rekursiver
Datalog-Regeln
 Falls in qi(...,c,...) eine Konstante c an der j-ten Stelle vorkommt,
füge die Bedingung
$j = c
zu Fi hinzu.
 Falls eine Variable X mehrfach an Positionen k und l in
qi(...,X,...,X,...) vorkommt, füge für jedes solches Paar die
Bedingung
$k = $l
zu Fi hinzu.
Auswertung nicht-rekursiver
Datalog-Regeln
Für eine Variable Y, die nicht in den normalen Prädikaten der
Regel vorkommt, gibt es zwei Möglichkeiten:
 Y kommt nur in einem Prädikat
Y=c
für eine Konstante c vor. Dann wird eine einstellige Relation mit
einem Tupel
QY := Y$1{[c]}
für dieses Prädikat gebildet.
 Y kommt in einem Prädikat
X=Y
vor, und X kommt in einem normalen Prädikat qi(…,X,…) an
k—ter Stelle vor. In diesem Fall setze
QY := Y$k ($k (Qi)) .
Auswertung nicht-rekursiver
Datalog-Regeln
 Bilde den natürlichen Verbund aller so entstandenen
Teilausdrücke:
E := E1
…
En
 Berechne dann F(E), wobei F die Konjunktion der Vergleiche
X  Y ist), die im Regelkörper vorkommen.
 Abschließend projiziere auf die Attribute, die als
Variablennamen im Kopf der Regeln (hier: p(X1,…Xm))
auftauchen:
 X1,…,Xm (F(E))
 Sollte p über mehrere Regeln definiert sein, vereinige die
entstandenen Algebraausdrücke via .
Beispiel: Nahe verwandte Vorlesungen
(r1) nvV(N1,N2) :- gV(N1,N2).
(r2) nvV(N1,N2) :- gV(M1,M2),vs(M1,N1),vs(M2,N2).
Dieses Beispielprogramm baut auf dem Prädikat gV auf und
ermittelt nahe verwandte Vorlesungen, die einen gemeinsamen
Vorgänger erster oder zweiter Stufe haben.
Er1 :=  N1$1,N2$2 ( $1,$2 ( TRUE (GV($1,$2))))
Kürzer: Er1 := GV(N1,N2)
Er2 := GV(M1,M2)
Ergebnis:
Vs(M1,N1)
Er1  Er2
Vs(M2,N2)
Auswertung rekursiver Regeln
(hier: Prädikat aufbauen)
a(V,N) :- vs(V,N).
a(V,N) :- a(V,M),vs(M,N).
Aufbauen
V
5001
5001
5001
5041
5041
5043
5052
5001
5001
5001
5041
5043
N
5041
5043
5049
5216
5052
5052
5259
5216
5052
5259
5259
5259
Auswertung rekursiver Regeln
Betrachten wir das Tupel [5001, 5052] aus der Relation Aufbauen.
Dieses Tupel kann wie folgt hergeleitet werden:
1.
2.
a (5001, 5043) folgt aus der ersten Regel, da
vs (5001, 5043) gemäß der EDB-Relation Voraussetzen gilt.
a(5001, 5052) folgt aus der zweiten (rekursiven) Regel, da
a)
a(5001, 5043) nach Schritt 1. gilt und
b) vs(5043, 5052) gemäß der EDB-Relation Voraussetzen gilt.
Zur Auswertung von a() benötigen wir also Tupel aus a()
selbst, die zuvor berechnet wurden.
"Naive" Auswertung durch Iteration
 Grundidee: IDB-Relationen schrittweise bestimmen. Starte mit
leerer IDB-Relation, füge auf Basis schon bekannter Tupel
iterativ neue Tupel hinzu.
 Abbruch der Iteration sobald Fixpunkt erreicht.
A(V,N) = Vs(V,N)  V,N (A(V,M)
Vs(M,N))
A := {};
repeat
A' := A;
A := Vs(V,N);
/* Regel 1 */
A := A  V,N (A'(V,M)
Vs(M,N)) /* Regel 2*/
until A' = A; /* Fixpunkt erreicht? */
output A;
"Naive" Auswertung durch Iteration
Iterationen:
1. Im ersten Durchlauf werden nur die 7 Tupel aus Voraussetzen
nach A "übertragen", da der Join leer ist (das linke Argument
A' des Joins wurde zur leeren Relation {} initialisiert).
2. Im zweiten Schritt kommen zusätzlich die Tupel [5001,5216],
[5001,5052], [5041,5259] und [5043,5259] hinzu.
3. Jetzt wird nur noch das Tupel [5001,5259] neu generiert.
4. In diesem Schritt kommt kein neues Tupel mehr hinzu, so dass
die Abbruchbedingung A' = A erfüllt ist.
(Naive) Auswertung der rekursiven
Regel für Prädikat aufbauen
Schritt
A
1
[5001,5041], [5001,5043],
[5001,5049], [5041,5216],
[5041,5052], [5043,5052],
[5052,5259]
[5001,5041], [5001,5043],
[5001,5049], [5041,5216],
[5041,5052], [5043,5052],
[5052,5259]
[5001,5216], [5001,5052],
[5041,5259], [5043,5259],
[5001,5041], [5001,5043],
[5001,5049], [5041,5216],
[5041,5052], [5043,5052],
[5052,5259]
[5001,5216], [5001,5052],
[5041,5259], [5043,5259],
[5001,5259]
wie in Schritt 3 (keine
Veränderung, also Terminierung
des Algorithmus
2
3
4
Der Wiener Kreis
5259
Wissenschaftstheorie
5052
Erkenntnistheorie
5043
Bioethik
5216
Ethik
5041
Grundzüge
5001
Mäeutik
5049
Inkrementelle (semi-naive)
Auswertung rekursiver Regeln
 Während der iterativen Auswertung des rekursiven Prädikates p
sei folgende Regel für die Generierung eines neuen Tupels t
"verantwortlich":
p(…) :- q1(…), …, qn(…).
 In der iterativen Auswertung wurde dazu ein RelationenalgebraAusdruck der Form
E(Q1
…
Qn)
ausgewertet.
 Das neue Tupel t entstehe in Iteration k auf Basis der Tupel
t1  Q1, …, tn  Qn. Dann muss eines dieser ti  Qi in Iteration
(k-1) neu generiert worden sein. Seien Qi die in Iteration
(k-1) erstmals generierten Tupel. Dann wird t also auch von
diesem Ausdruck erzeugt:
E(Q1
… Qi …
Qn)
Inkrementelle (semi-naive)
Auswertung rekursiver Regeln
 Aber aus welchem spezifischen Qi stammt dieses Tupel ti?
 Betrachte die  aller Subgoal-Relationen gesondert.
Berechne:
E(Q1
… Qi …
Qn)
 … E(Q1
…
Qi
E(Q1
…
Qi
…
…
Qn)  … 
Qn)
 In jedem Teilausdruck der Vereinigung darf jeweils nur ein 
einer Subgoal-Relation eingesetzt werden. Falls die t1,…,
ti-1,ti+1,…,tn in Schritten < k erzeugt wurden, ist sichergestellt,
daß t durch
E(Q1
… Qi …
Qn)
erzeugt wird.
Inkrementelle (semi-naive)
Auswertung rekursiver Regeln
 Beispiel: In der iterativen Auswertung von Prädikat aufbauen
(Relation A), wurde folgendes Tupel t in der 3. Iteration
generiert:
t = [5001, 5259]
 Tupel t entstand aus dem folgenden Join zweier Tupel:
[ 5001, 5052 ]
[ 5052, 5259 ]
Dabei wurde [ 5001, 5052 ]  A in Iteration 2 generiert. Tupel
[ 5052, 5259 ] ist der Teil der (invarianten) EDB-Relation Vs.
Algorithmus zur semi-naiven
Auswertung von Prädikat aufbauen
1. Vs(V,N) := {};
2. A(V,N) := Vs(V,N);
3. A(V,N) := A(V,N)   V,N (A(V,M)
Vs(M,N));
4. A(V,N) := A(V,N);
5. repeat
6.
A' (V,N):= A(V,N); /* A': im letzten Schritt neu gen. Tupel */
7.
A(V,N) := Vs(V,N);
8.
A(V,N) := A(V,N) 
9.
V,N (A'(V,M)
Vs(M,N)) 
10.
V,N (A(V,M)
Vs(M,N));
11.
A(V,N) := A(V,N) \ A(V,N); /* nur tatsächlich neue Tupel */
12.
A(V,N) := A(V,N)  A(V,N); /* akkumuliere Endergebnis */
13. until A(V,N) = {};
Bemerkung: Vs(V,N) bleibt während der Berechnung {}
(EDB-Relationen sind invariant).
Illustration der semi-naiven
Auswertung von aufbauen
Schritt
Initialisierung
(Zeile 2. und 3.)
1. Iteration
2. Iteration
3. Iteration
A
(7 Tupel aus Vs:)
[5001,5042], [5001,5043]
[5043,5052], [5041,5052]
[5001,5049], [5001,5216]
[5052,5259]
(Pfade der Länge 2)
[5001,5216], [5001,5052]
[5041,5259], [5043,5259]
(Pfade der Länge 3)
[5001,5259]
{}
(Terminierung)
Bottom-Up oder Top-Down
Auswertung?
Die bisher beschriebene bottom-up Auswertung leitet die IDB
aus den EDB-Relationen ab.
(Optimierbare) Ausdrücke der relationalen Algebra berechnen
neue Tupel der IDB aus vorhergehenden Ableitungen.
Achtung: Es wird aber jeweils die gesamte IDB abgeleitet 
obwohl für Beantwortung einer Query oft ein Ausschnitt
ausreichend ist:
(r1)
(r2)
a (V, N) :- vs (V, N).
a (V, N) :- a (V, M), vs (M, N).
query (V ) :- a (V, 5052).
Relevanter Ausschnitt der EDB-Relation
Voraussetzen für query(V) :- a(V, 5052)
5259 (WienerKreis)
5216 (Bioethik)
5052 (Wiss. Theorie)
5041 (Ethik)
5043 (Erk. Theorie)
5001 (Grundzüge)
5049 (Mäeutik)
Rule/Goal-Baum zur Top-Down
Auswertung
a(V,5052)
(r1) a(V,5052) :- vs(V,5052)
(r2) a(V,5052) :- a(V,M1),vs(M1,5052)
Bindungen für
V aus EDB
vs(V,5052)
(r1) a(V,M1) :- vs(V,M1)
vs(V,M1)
a(V,M1)
vs(M1,5052)
(r2) a(V,M1) :- a(V,M2),v2(M2,M1)
a(V,M2)
:
vs(M2,M1)
Rule/Goal-Baum mit Auswertung
a(V,5052)
(r1) a(V,5052) :- vs(V,5052)
vs(V,5052)
(r2) a(V,5052) :- a(V,M1),vs(M1,5052)
a(V,M1)
V  {5041,5043}
(r1) a(V,M1) :- vs(V,M1)
vs(V,M1)
V  {5001}
vs(M1,5052)
M1  {5041,5043}
(r2) a(V,M1) :- a(V,M2),v2(M2,M1)
a(V,M2)
vs(M2,M1)
:
M2  {5001}
VØ
Negation () im Regelrumpf und
Stratifikation
indirektAufbauen(V,N) :- aufbauen(V,N), voraussetzen(V,N).
Eine Regel r mit einem negierten Prädikat im Rumpf, wie z.B.
r  p (...) :- q1 (...), ..., qi (...), ..., qn (...).
kann nur dann sinnvoll ausgewertet werden, wenn Relation Qi
schon vollständig materialisiert ist (t  Qi?). Dazu müssen
zuerst alle Regeln mit Kopf
qi (...) :- ... ausgewertet sein.
Das ist nur möglich, falls qi nicht abhängig von p ist.
Also darf der Abhängigkeitsgraph keine Pfade von qi nach p
enthalten. Wenn das für alle Regeln und negierten Subgoals der
Fall ist, ist das Datalog-Programm stratifiziert.
Achtung, Sicherheit: In qi (…,V,…) ist Variable V nicht
beschränkt. (Warum?)
Beispiel: Auswertung einer Regel
mit Negation
 Auszuwertende Regel (ist das Programm stratifiziert?):
iA (V,N) :- a (V,N), vs (V,N).
 Ausdruck der relationalen Algebra hierzu:
IA (V,N) =  V,N ( A (V,N)
=* A(V,N)
Vs (V,N) )
- Vs (V,N)
Berechnung von IA(V,N) jetzt einfach aus Basis von bereits
materialsierter IDB-Relation A(V,N) und EDB-Relation Vs(V,N).
Wieso gilt eigentlich =* ?
Komplexeres Beispiel: Regel mit
Negation
grundlagen(V) :- voraussetzen(V,N).
spezialVorl(V) :- vorlesungen(V,T,S,R),  grundlagen(V).
 Äquivalente Ausdrücke der relationalen Algebra:
Grundlagen(V) = V (Voraussetzen(V,N))
SpezialVorl(V) = V (Vorlesungen(V,T,S,R)
Grundlagen(V))
 Wie ist hier das Komplement von Grundlagen(V) zu bestimmen?
(Projektion V unter den
verschieben: projection pushdown)
 Falls pushdown unmöglich ist: Konstruktion der aktiven
Domäne (DOM, s. Buch).
Ausdruckskraft von Datalog
 Die Sprache Datalog, eingeschränkt auf nicht-rekursive
Programme aber erweitert um Negation, wird in der Literatur
manchmal als Datalog non-rec bezeichnet
 Diese Sprache Datalog non-rec hat genau die gleiche
Ausdruckskraft wie die relationale Algebra – und damit
ist sie hinsichtlich Ausdruckskraft auch äquivalent zum
relationalen Tupel- und Domänenkalkül.
 Datalog mit Negation und Rekursion geht natürlich über die
Ausdruckskraft der relationalen Algebra hinaus – man konnte in
Datalog ja z.B. die transitive Hülle der Relation Voraussetzen
definieren (repeat … until nicht in relationaler Algebra
verfügbar).
Simulation der relationalen Algebra
in Datalog
 Selektion
 SWS > 3 (Vorlesungen)
 Titel = "Mäeutik" (Vorlesungen)
In Datalog:
query1(V,T,S,R) :- vorlesungen(V,T,S,R), S > 3.
query2(V,T,S,R) :- vorlesungen(V,"Mäeutik",S,R).
 Projektion
 Name, Rang (Professoren)
In Datalog:
query(Name,Rang) :- professoren(PersNr,Name, Rang, Raum).
Simulation der relationalen Algebra
in Datalog
 Kreuzprodukt
Professoren  Vorlesungen
In Datalog:
query(V1,V2,V3,V4,P1,P2,P3,P4) :- professoren(P1,P2,P3,P4),
vorlesungen(V1,V2,V3,V4).
 -Join (hier mit Projektion)
Titel,Name(Vorlesungen gelesenVon=PersNr Professoren)
In Datalog:
query(T,N) :- vorlesungen(V,T,S,R), professoren(R,N,Rg,Ra).
Simulation der relationalen Algebra
in Datalog
 Vereinigung (von Relationen identischer Schemata)
 PersNr, Name (Assistenten)   PersNr,Name (Professoren)
In Datalog:
query(PersNr,Name) :- assistenten(PersNr,Name,F,B).
query(PersNr,Name) :- professoren(PersNr,Name,Rg,Ra).
 Differenz
VorlNr (Vorlesungen)  VorlNr (Voraussetzen)
In Datalog:
query1(V) :- vorlesungen(V,T,S,R).
query2(V) :- voraussetzen(V,N).
query(V) :- query1(V),  query2(V).