Physik 1. Verformung fester Körper (technische Mechanik)
Werbung

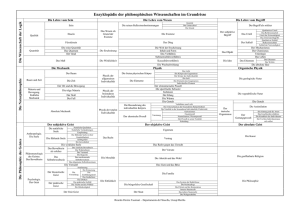
Physik verformbare Körper Physik 1. Verformung fester Körper (technische Mechanik) WS 15/16 | 1. Sem. | B.Sc. Oec. und B.Sc. CH | 10.2015 | Physik 1 | technische Mechanik | Großmann | 3 Physik Verformung fester Körper Themen • Anwendungsbeispiele • Physikalische Modellvorstellung • Berechnung der Materialeigenschaften • Zugspannung • Druckspannung • Torsionsspannung | 10.2015 | Physik 1 | technische Mechanik | Großmann | 5 Physik verformbare Körper Anwendungen Anwendungen • Lebensmittel • • • • Schnittkäse Nudeln (Master) Knäckebrot (IP II) Verpackungen • sicherer Transport • • • • leicht und sicher zu öffnen • • • Stöße Durchdringen Bruchfestigkeit (IP II) Verschlüsse Folien Maschinen und Material • • auftretende Belastungen Belastungsgrenzen kennen und beachten | 10.2015 | Physik 1 | technische Mechanik | Großmann | 6 Physik verformbare Körper Anwendungen Beispiel Verpackung (1/2) | 10.2015 | Physik 1 | technische Mechanik | Großmann | 7 Physik verformbare Körper Anwendungen Beispiel Verpackung (2/2) | 10.2015 | Physik 1 | technische Mechanik | Großmann | 8 Physik verformbare Körper Modellvorstellung Modellvorstellung eines Festkörpers • Festkörper sind • formstabil • elastisch • • Kugelmodell (Vorlesung Wärme, Versuch VIS im IP 2) unzureichend, muss für Festkörper erweitert werden Idealisierte Grundform eines Festkörpers: Kristall • Regelmäßige Struktur • Liegt bei allen Metallen vor • 80% aller natürlichen Elemente sind Metalle | 10.2015 | Physik 1 | technische Mechanik | Großmann | 9 Physik verformbare Körper Modellvorstellung Modellvorstellung Kristall (SP) • Atome als Kugeln • Bindungskräfte als Schraubenfedern • Äußerlich wirkende Kräfte bewirken kleine Abstandsänderungen zwischen den Atomen • Hooke‘sches Gesetz anwendbar Festkörper | 10.2015 | Physik 1 | technische Mechanik | Großmann | 10 Physik verformbare Körper Verformungsarten Welche Verformungen gibt es? • Reale Festkörper ändern ihre Form unter der Wirkung von • • • • • Druck Zug Schub (Scherung) Torsion (Verdrehung) Biegen (wird hier nicht weiter betrachtet) • Dabei wirkt eine Kraft auf die (Ober)Fläche des Körpers | 10.2015 | Physik 1 | technische Mechanik | Großmann | 12 Physik verformbare Körper Verformungsarten Mechanische Spannung • Kraft pro Fläche wird bei Verformungen als mechanische Spannung bezeichnet, gemessen in N/m² oder Pa*). Zerlegbar in • Kraft senkrecht zur Oberfläche: Normalspannungen Beispiele • • • Kraft parallel zur Oberfläche: Tangentialspannung Beispiele • • • Zug Druck Schub Torsion Für kleine Verformungen gilt • • *) Hooke‘sches Gesetz in unterschiedlichen Formen „Die Verformung ist proportional zur wirkenden Spannung“ nach Blaise Pascal, 1623 – 1662, französischer Philosoph, Physiker und Mathematiker | 10.2015 | Physik 1 | technische Mechanik | Großmann | 13 Physik verformbare Körper Verformungsarten Auswirkungen der Verformungen • Die Auswirkungen einer Verformung hängen ab vom • Material • Stärke der Verformung • • • elastische Verformung plastische Verformung Bruch • Wo liegen die Belastungsgrenzen für Geräte(teile)? Versuch KUE, IP 2 | 10.2015 | Physik 1 | technische Mechanik | Großmann | 14 Physik verformbare Körper Verformungsarten Elastische Verformung • Verformung bleibt nur solange bestehen wie die Spannung wirkt (reversibel) • Keine Umwandlung von mechanischer Energie in Wärme • Jeder Festkörper lässt sich in bestimmten Grenzen elastisch verformen • Wissenswert: Wo ist die (materialabhängige) Grenze? • Beispiel: Gummiband | 10.2015 | Physik 1 | technische Mechanik | Großmann | 15 Physik verformbare Körper Verformungsarten Plastische Verformung • Bei Überschreitung der Elastizitätsgrenze tritt eine bleibende (irreversibele) Formänderung ein • Plastische Verformung liegt vor, solange kein Bruch entsteht | 10.2015 | Physik 1 | technische Mechanik | Großmann | 16 Physik verformbare Körper Verformungsarten Bruch • Brüche entstehen durch • Überschreitung der Plastizitätsgrenze (z.B. Einkerbung, Überdehnung) • wiederholte Verformung z.B. durch Hin- und Herbiegen eines Drahts (Ermüdungsbruch) • Die Festigkeit eines Materials ist abhängig von • Belastungsart: Welche Art von Verformung liegt vor? • Belastungsdauer: besteht die Verformung kurzoder langzeitig? | 10.2015 | Physik 1 | technische Mechanik | Großmann | 17 Physik verformbare Körper Materialeigenschaften 18 BERECHNUNG DER MATERIALEIGENSCHAFTEN Zugspannung | 10.2015 | Physik 1 | technische Mechanik | Großmann | Physik verformbare Körper Verformungsarten Bungee Jumping • • • Nach dem Absprung kommt es zum freien Fall, solange das Gummiseil nicht gestrafft ist. Durch das Straffen wird das Gummiseil gedehnt, bis die dadurch entstehende Kraft den Fall vollständig abgebremst hat (Hooke‘sches Gesetz) Das Seil muss auf das Gewicht der springenden Person abgestimmt werden. | 10.2015 | Physik 1 | technische Mechanik | Großmann | Quelle: Wikipedia 19 Physik verformbare Körper Verformungsarten Verformung durch Zugspannung • Die Zugspannung • verlängert einen Körper in Richtung der Zugspannung • vermindert den Durchmesser des Köpers quer zur Richtung der Zugspannung (Querkontraktion) • vergrößert das Volumen des Körpers | 10.2015 | Physik 1 | technische Mechanik | Großmann | 20 Physik verformbare Körper Verformungsarten 21 Zugspannung in der Modellvorstellung ungestörter Festkörper (FK) | 10.2015 | Physik 1 | technische Mechanik | Großmann | plastisch verformter FK elastisch verformter FK Physik verformbare Körper Verformungsarten Hooke‘sche Gesetz für Längenänderung (SP) L : Längenänderung in m L0 : Anfangslänge in m • • • • : Zugspannung in Pa : Elastizitätsmodul in Pa Elastizitätsmodul E ist eine Materialkonstante Elastizitätsmodul von Festkörpern ist groß (1011 N/m²). Die Längenänderung daher gering. Ursache der Längenänderung ist eine Kraft, keine Temperaturänderung! | 10.2015 | Physik 1 | technische Mechanik | Großmann | E 23 Physik verformbare Körper Verformungsarten 24 Aufgabe Bungee Sprung • • Beim Sprung von der Europabrücke wird nach einem freien Fall das Gummiseil von 40 m auf 170 m gedehnt. Berechnen Sie • • • die Geschwindigkeit v nach dem Fall von 40 m. Berechnen Sie die Beschleunigung (Verzögerung) a, wenn der Fall nach 170 m gestoppt ist. Welche Größen benötigen Sie noch, um das richtige Gummiseil für die Person zu wählen? | 10.2015 | Physik 1 | technische Mechanik | Großmann | Europabrücke Quelle: Wikipedia Physik verformbare Körper Verformungsarten Lösung Bungee Sprung | 10.2015 | Physik 1 | technische Mechanik | Großmann | 25 Physik verformbare Körper Verformungsarten Bungee Seil • Wie verändert sich sein Durchmesser? • Qualitativ: Durchmesser wird durch die Querkontraktion geringer (vgl. Folie 20) • Beispiel: Gummiband • Quantitativ: Ohne weitere Informationen keine Aussage möglich | 10.2015 | Physik 1 | technische Mechanik | Großmann | 26 Physik verformbare Körper Verformungsarten Querkontraktion (SP) • Hooke‘sche Gesetz für die Längenänderung ergibt keine Aussage über die Querkontraktion d • Verhältnis der relativen Querkontraktion d/d0 zur relativen Längenänderung L/L0 ist eine Materialkonstante (Poisson-Zahl ) | 10.2015 | Physik 1 | technische Mechanik | Großmann | 28 Physik verformbare Körper Verformungsarten Aufgabe Längenänderung • Gegeben sei ein Kupferzylinder mit einer Länge L = 10 cm und einem Querschnitt d = 1 cm. Der Zylinder wird um 0,1% gelängt. a. Wird die Festigkeitsgrenze F überschritten? b. Wie verändert sich sein Querschnitt d? c. Wie ändert sich das Volumen V? • Materialkonstanten für weiches Kupfer: • E = 1,26•1011 N/m² • = 0,35 • F = 0,45•109 N/m² | 10.2015 | Physik 1 | technische Mechanik | Großmann | 29 Physik verformbare Körper Verformungsarten Lösung Längenänderung (SP) | 10.2015 | Physik 1 | technische Mechanik | Großmann | 30 Physik verformbare Körper Verformungsarten BERECHNUNG DER MATERIALEIGENSCHAFTEN DRUCKSPANNUNG | 10.2015 | Physik 1 | technische Mechanik | Großmann | 31 Physik verformbare Körper Verformungsarten Verformung durch Druckspannung • Volumenverkleinerung/-vergrößerung durch erhöhten bzw. niedrigeren Druck (Volumenelastizität) • Beispiel: Festkörper in Flüssigkeit • Druck wirkt immer senkrecht auf die Oberfläche des Körpers • Das Volumen nimmt proportional zum steigenden Druck ab | 10.2015 | Physik 1 | technische Mechanik | Großmann | 32 Physik verformbare Körper Verformungsarten 33 Modellvorstellung Druckspannung ungestörter Festkörper | 10.2015 | Physik 1 | technische Mechanik | Großmann | komprimierter Festkörper Physik verformbare Körper Verformungsarten Hooke‘sche Gesetz für Volumenänderung (SP) V : V0 : p : K : • • • • • Volumenänderung in m³ Anfangsvolumen in m³ Druck(spannung) in Pa Kompressionsmodul in Pa V < 0, da Druckzunahme das Volumen verkleinert Kompressionsmodul K ist eine Materialkonstante Kompressionsmodul von Festkörpern ist groß (1011 N/m²). Die Volumenänderung daher gering. In der Technik übliche Einheit: 105 N/mm2 Ursache der Volumenänderung ist eine Kraft, keine Temperaturänderung! | 10.2015 | Physik 1 | technische Mechanik | Großmann | 35 Physik verformbare Körper Verformungsarten Aufgabe Volumenänderung (SP) • Wie verändert sich das Volumen einer Kupferkugel ( =1,40•1011 N/m²), wenn der Druck um 1.000 Bar (= 108 Pa) zunimmt? | 10.2015 | Physik 1 | technische Mechanik | Großmann | 36 Physik verformbare Körper Verformungsarten Lösung Volumenänderung (SP) | 10.2015 | Physik 1 | technische Mechanik | Großmann | 37 Physik verformbare Körper Verformungsarten Beispiel Volumenänderung • Wie verändert sich das Volumen einer Kupferkugel ( =1,40•1011 N/m²), wenn der Druck um 1.000 Bar (= 108 Pa) zunimmt? • Zum Vergleich: Die gleiche Volumenänderung würde durch eine Abkühlung von 14 K erreicht! | 10.2015 | Physik 1 | technische Mechanik | Großmann | 38 Physik verformbare Körper Materialeigenschaften BERECHNUNG DER MATERIALEIGENSCHAFTEN SCHUBSPANNUNG | 10.2015 | Physik 1 | technische Mechanik | Großmann | 39 Physik verformbare Körper Materialeigenschaften Verformung durch Schubspannung • Schubspannung kann als Scherung oder als Torsion auftreten • Kraft greift tangential am Körper an • Die Gestalt des Körpers ändert sich • Das Volumen bleibt unverändert | 10.2015 | Physik 1 | technische Mechanik | Großmann | 40 Physik verformbare Körper Materialeigenschaften 41 Schubspannung in der Modellvorstellung ungestörter elastisch Festkörper (FK) verformter FK | 10.2015 | Physik 1 | technische Mechanik | Großmann | plastisch verformter FK Physik verformbare Körper Materialeigenschaften Hooke‘sche Gesetz für Scherung (SP) G : Schubmodul [N/m 2 ] • Die Schubspannung bewirkt bei einem Würfel, bei dem die Kräfte F an der Fläche A der Ober- oder Unterseite angreifen, eine Scherung • Die Oberseite wird gegenüber der Unterseite verschoben • Die senkrechten Kanten werden um einen Winkel gekippt • Für kleine Winkel ( in rad!) gilt das Hooke‘sche Gesetz • Schubmodul G ist eine Materialkonstante (1011 N/m²) | 10.2015 | Physik 1 | technische Mechanik | Großmann | 43 Physik verformbare Körper Materialeigenschaften Beispiele Scherung • Schwämme bei der Reinigung von Oberflächen (reversibel) • Schneiden mit Schere/Messer (irreversibel) | 10.2015 | Physik 1 | technische Mechanik | Großmann | 44 Physik verformbare Körper Materialeigenschaften Torsion • Zwei entgegengesetzte Drehmomente verdrehen die Endflächen z.B. bei einem Zylinder • Der Zylinder wird um einen Winkel axial verdreht (tordiert) • Gedachte senkrechte Linien auf der Zylinderoberfläche werden um einen Winkel gekippt | 10.2015 | Physik 1 | technische Mechanik | Großmann | 45 Physik verformbare Körper Materialeigenschaften 47 Erforderliches Drehmoment (SP) • Für kleine Winkel ( in rad!) gilt T : Drehmoment in Nm G : Schubmodul in N/m 2 R : Radius des Zylinders in m L : Länge des Zylinders in m : Drehwinkel in rad | 10.2015 | Physik 1 | technische Mechanik | Großmann | Physik verformbare Körper Materialeigenschaften Beispiele Torsion | 10.2015 | Physik 1 | technische Mechanik | Großmann | 48 Physik verformbare Körper Materialeigenschaften Aufgabe Torsion • Ein Rührer wird über eine 10 mm starke und 1 m lange V2A-Achse (G = 81010 N/m2) von einem Motor angetrieben. • Wie groß darf das Drehmoment des Motors maximal sein, wenn die Achse um maximal 5° tordiert werden soll? • Um welchen Faktor würde sich das maximal zulässige Drehmoment verändern, • • wenn die Achse 20 mm stark wäre? wenn die Achse 1,5 m lang wäre | 10.2015 | Physik 1 | technische Mechanik | Großmann | 49 Physik verformbare Körper Materialeigenschaften Lösung Torsion (SP) | 10.2015 | Physik 1 | technische Mechanik | Großmann | 50