W - KIT

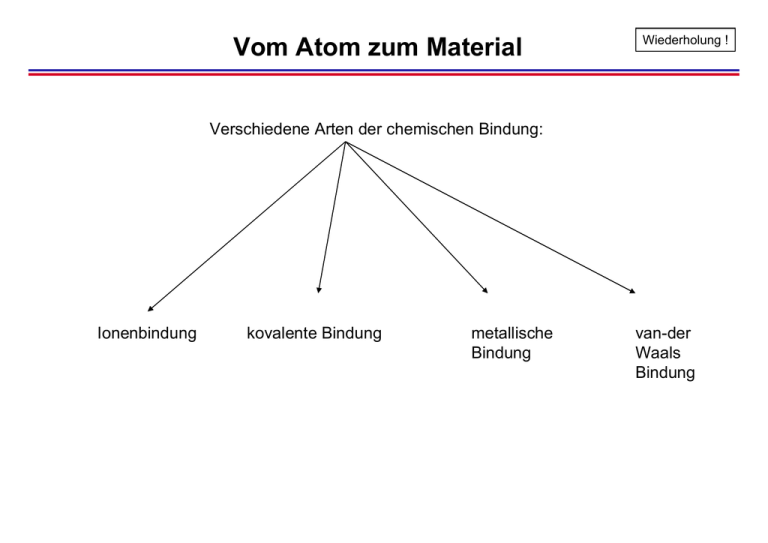
Vom Atom zum Material
Wiederholung !
Verschiedene Arten der chemischen Bindung:
Ionenbindung
kovalente Bindung
metallische
Bindung
van-der
Waals
Bindung
Vom Atom zum Material: Die Ionenbindung Wiederholung !
Na: 1s22s22p63s1
Cl: 1s22s22p63s23p5
Energetische Betrachtung:
Ionisierungsenergie: Na+5.1eV=Na++e
Elektronenaffinität: Cl+e=Cl-+3.6eV
Nettoaufwand: 1.5 eV
Wiederholung !
Vom Atom zum Material: Die kovalente Bindung
Variation des Kernabstandes:
Gebundener Zustand beim Energieminimum
E
anti-bindend
antiE1S
bindend
Energiegewinn pro Atom
bei Si: 4.64 eV
Wiederholung !
Vom Molekül zum Festkörper
Verallgemeinerung von zwei auf 1023 Atome
Energiezustände des Gitters
Wiederholung !
Temperatur = 0 K:
Aufspaltung der
Energiezustände
Für N Atome Aufspaltung in
N Energiezustände
Diese energetisch nahe
zusammenliegenden
Zustände bilden “Bänder”
von erlaubten Zuständen.
Komplexes Verhalten durch
Überkreuzungen
Kristallstruktur von Si und Ge
Wiederholung !
Si und Ge bilden Diamantgitter
Die Diamantstruktur hat ein fcc-Gitter mit einer Einheitszelle, die aus
zwei Atomen bei (0,0,0) und (1/4,1/4,1/4)a besteht. a ist die Länge der
Einheitszelle.
z.B. Si, Ge
z.B. GaAs
Periodische Potentiale
Wiederholung !
Periodische Anordnung von Atomen → Periodisches Potential V(x)
Schematische Darstellung eines
quantenmechanischen Elektrons in
einem periodischen Potential eines
kristallinen Festkörpers
Drastische Effekte, wenn die halbe Wellenlänge der Elektronen (oder ein
ganzzahliges Vielfaches) gleich der Periode des Potentials ist
Ausbildung von stehenden Wellen
Wiederholung !
Vom freien Elektron zum Kristallelektron
E
-π/a
π/a
Dispersionsrelation
des freien Elektrons
=2k 2
E =
2m
gestreute
Teilwellen
einfallendes
Elektron
a
a
a
Konstruktive Überlagerung
der Teilwellen falls λ/2=a
oder k=π/a
Wiederholung !
Vom freien Elektron zum Kristallelektron
c) Ψ*Ψ(x) obere „Bandkante“
b) Ψ*Ψ(x) untere „Bandkante“
Dispersionsrelation
des Kristallelektrons
Aufspaltung der
Parabeläste bei IkI=π/a, Ausbildung von
stehenden Wellen
-bei einer Wellenlänge zwei qualitativ
unterschiedliche Möglichkeiten
die stehende Welle im Verhältnis zu den
Atomrümpfen zu platzieren.
Periodische Bandstruktur
Wiederholung !
Es genügt, den Bereich von -0.5K bis 0.5K darzustellen. Diesen Bereich
nennt man die erste Brillouin-Zone.
Einfachere
Darstellung
Wiederholung !
Bloch-Elektronen
GG
G
G
ikr
Ψ nk (r ) = e unkG (r )
http://fermi.la.asu.edu/ccli/applets/kp/kp.html
Richtungsabhängigkeit des Potentials
Bisher haben wir nicht bedacht, dass das Potential für die verschiedenen
Raumrichtungen verschieden ist.
Nehmen wir z.B. an wir haben ein 2D-Gitter. Die Atome sind entlang der
X-Richtung näher zusammen als entlang der L-Richtung.
Daher erwarten wir, dass durch den unterschiedlichen Potentialverlauf
auch die Energiezustände unterschiedlich sind.
z.B. beim quadratischen
Gitter in 2D:
X
L
Γ
Γ: K=(0,0)
X: K=(0,1)
L: K=(1,1)
Richtungsabhängigkeit des Potentials
In der Tat zeigen Berechnungen, dass die Energiezustände
richtungsabhängig sind.
Oft werden deshalb in einem Bandstruktur-Diagramm die
Energiezustände für verschiedene relevante Richtungen gezeigt:
Γ
K=(0,0)
X
Γ
L
K=(0,1)
(0,0)
k=K(1,1)
L
Γ X
Bandstruktur von Silizium
Darstellung der Eigenzustände in
Bandstrukturen. Gibt wieder die
Abhängigkeit von ω (bzw. W ) von
k an. Allerdings handelt es sich
nicht mehr um einzelne ebene
Wellen sondern um komplexe
Überlagerungen.
Die neuen Eigenzustände heissen
Blochzustände.
Bandstruktur von Germanium
Bandstruktur von GaAs
Elektronische Eigenschaften von Halbleitern
•
In der Vorlesung “Elektronische Schaltungen” haben Sie das Verhalten
verschiedener Halbleiterbauelemente kennen gelernt:
– Dioden, Bipolare Transistoren, Feldeffekttransistoren
Source: ES-Skript
•
•
Warum verhalten sich die Bauelemente so ?
Wie designt man neuartige Bauelemente ?
Beweglichkeit von Kristallelektronen
•
Wie bewegen sich Elektronen in Kristallen?
HL
E
makroskopisch:
J = σE
bzw.
JG
JG
J = σE
Wie berechnet man σ ??
Geschwindigkeit von Materiewellen
JG
E
Gruppengeschwindigkeit
(Geschwindigkeit, mit der
sich der
Schwerpunkt eines
Wellenpaketes bewegt)
∂ω
vg =
∂k
Abb.: Wellenpaket im periodischen Potential
Dieser Zusammenhang gilt
auch für Blochelektronen !
Lassen wir also einmal ein elektrisches Feld
auf ein Wellenpaket einwirken ...
Beschleunigung von Materiewellen
Für die Gruppengeschwindigkeit gilt:
vg =
∂ω 1 ∂W (k )
=
;
∂k = ∂k
Ziel: Ableitung einer Bewegungsgleichung für ein
Elektron im Kristall:
Klassische Änderung der Energie pro infinitesimaler Zeiteinheit:
dW
= F ⋅v
dt
für ein Blochelektron:
...um W zu ändern, muss k
geändert werden
dW 1 ∂W (k ) d ( =k )
=
dt
=
∂k
dt
D.h. äußere Kraft verschiebt den k-Vektor des
Wellenpaketes gemäß
vg
dk 1
= F
dt =
Beschleunigung von Materiewellen
Wie sieht es mit der Beschleunigung aus ?
1 d ⎛ ∂W
=
a=
= dt ⎜⎝ ∂k
dt
dv g
2
⎛
∂
W
1
⎞
⎟ = =⎜ 2
⎠
⎝ ∂k
⎞ dk
1 ⎛ ∂ 2W
= 2⎜ 2
⎟
⎠ dt = ⎝ ∂k
⎞
⎟F
⎠
Analog zum klassischen F=ma kann also eine Masse des
Blochelektrons definiert werden:
1
1 ∂ W (k )
= 2
*
=
∂k 2
m
⎛ ∂ W (k ) ⎞
m* = =2 ⎜
⎟
2
⎝ ∂k
⎠
2
2
bzw.
-1
„Masse“ des Kristallelektrons wird bestimmt durch die Bandstruktur !!!
Elektronen in Kristallen
•
Transporteigenschaften von Kristallelektronen werden bestimmt durch
die Bandstruktur
•
(Gruppen)Geschwindigkeit ist
gegeben durch
1 ∂W (k )
vg =
;
= ∂k
•
Die effektive Masse dieser
Elektronen ist:
⎛ ∂ W (k ) ⎞
m == ⎜
⎟
2
∂
k
⎝
⎠
*
•
2
2
-1
Kristallelektronen benehmen sich
bei Beschleunigung wie Teilchen
der Masse m* (meff)!
W
Beispiel: Kosinusförmiges Band I (W(k)=E(k))
•
Bsp.: kosinusförmiges
Band
Beispiel: Kosinusförmiges Band II
•
Eine konst. Kraft F
bewirkt das folgende k(t):
in vg(t)
..und in x(t)
•
Nach diesem Modell erwarten wir eine oszillierende Bewegung der
Elektronen (Bloch-Oszillationen) mit einer Periode von ca. 0,8 ps.
Aber: Einfluss von Störungen
•
In einem realen Kristall wird die Bewegung des Elektrons
unterbrochen durch z.B.
– Stöße mit Gitterschwingungen (Wechselwirkung mit Phononen)
– Streuung an Defekten
– Elektron-Elektron-Streuung
•
Die Zeit τ für diese Störungen ist
typischerweise viel kürzer als die
Periode der Bloch-Oszillation.
•
Bloch-Oszillationen können nur in speziell hergestellten künstlichen
Kristallen beobachtet werden.
– THz-Technik
Ströme in Halbleitern
Strom im Halbleiter:
Abfolge von Phasen der Beschleunigung und abrupten Stößen
Elektronen werden durch den Halbleiter getrieben
„Drift“ströme
Elektronenbahn
ohne/mit Feld
Driftströme
Elektronen werden im Mittel nach der Zeit τ durch
Stoß mit Atomrumpf abrupt abgebremst.
Damit ergibt sich als mittlere Geschwindigkeit:
Damit ergibt sich eine zentrale Größe der
Halbleiterelektronik, die Beweglichkeit µ:
v=
F
qEτ −eEτ
τ= * =
≡ −µE
*
m
m
m
eτ
µ= *
m
Sie ist ein Maß dafür, wie schnell sich ein Elektron im Halbleiter unter
Einwirkung des elektrischen Feldes bewirkt
Driftströme
Stromdichte durch ein Volumenelement:
J = q ⋅ n ⋅v
mittlere Geschwindigkeit
Einheit: m/s
Ladung pro
Teilchen
(Einheit: C)
Dichte der Ladungen
(Einheit: m-3 bzw cm-3)
Die Stromdichte ist direkt proportional zur Beweglichkeit:
J = qnv = qnµE
-hohe Beweglichkeiten
-hohe Stromdichten
-geringe Schaltzeiten
GaAs Bandstruktur und Beweglichkeit
• Die effektive Masse der
Ladungsträger ist eine
Funktion des k-Wertes und
des Bandes.
• Die Zeitkonstante τ ist
ebenfalls nicht konstant.
• Deshalb ist die
Beweglichkeit nicht für alle
Elektronenzustände gleich.
Si Bandstruktur und Beweglichkeit
• Die Träger relaxieren durch
Stöße zu den niedrig
gelegenen Zuständen im Band.
• Deshalb heißt τ auch
Intrabandimpulsrelaxationszeit.
• Die Elektronenbeweglichkeit im
Leitungsband ist bei Si kleiner
als bei GaAs.
• Dies sieht man an der
geringeren Bandkrümmung im
Minimum.
eτ
µ=
m eff
Beweglichkeit in Si, Ge und GaAs
Source:[5]
• Elektronen hoher Energie haben z.B. eine geringere Beweglichkeit
Halbleiter mit hoher Beweglichkeit
Für Hochfrequenzbauelemente
(optische Nachrichtentechnik,
Mobilfunk) sind die Si-Elektronen
u. U. nicht schnell genug.
Erforschung und Einsatz von
anderen Halbleitermaterialien
z.B. GaAs, InP, SiGe
Quelle: Infineon Corporate Research
Halbleiter mit hoher Beweglichkeit
Quelle: Infineon Corporate Research
Beweglichkeiten
Die Beweglichkeit ist nicht naturgegeben:
Wird bestimmt durch:
- Reinheit des Halbleiters (wenige Streuprozesse)
- Wahl des Materials
- den k-Zustand (Energie) des Elektrons
Beweglichkeit in Si, Ge und GaAs
v = −µ E
eτ
µ=
m eff
Source:[5]
• Für kleine Feldstärken ist die Beweglichkeit der Ladungsträger und
die effektive Masse ungefähr konstant. In diesem Bereich ist die
Parabelnäherung zur Bandstruktur anwendbar.
Parabolische Näherung
• Da die Bandstruktur in diesen Bereichen symmetrisch ist, können wir
sie durch eine Parabel annähern.
• Die Elektronen verhalten sich wie freie Elektronen mit einer
konstanten effektiven Masse.
Direkter Halbleiter
z.B. GaAs
Indirekter Halbleiter
z.B. Si, Ge
Parabolische Näherung
W
=2 k 2
WC (k ) = WG +
2me
WG
me,h: Effektive Elektron(Loch)masse
G
G qE
a=
me,h
G
1
1 ∂ Wn (k )
= 2
me,h =
∂k 2
2
=2 k 2
WV = −
2mh
Parabelnäherung: Löcherbewegung
- Strombeiträge einzelner Elektronen in einem vollbesetzten Band
kompensieren sich paarweise:
- Strom wird nur getragen von teilweise gefüllten Bändern
Autobahn-Analogie
•
•
•
•
Wir wollen Pakete per Auto von Karlsruhe nach Frankfurt bringen.
Jedes Auto kann ein Paket mitnehmen.
Wenn wir kein Auto haben, können wir nichts transportieren.
Je mehr Autos wir auf die Straße schicken, desto mehr Pakete
können wir transportieren…. aber irgendwann gibt es einen Stau.
• Aber wenn alles voll
ist, geht auch nichts
mehr (Elektronen sind
Fermionen !)
Primitives Bändermodell
• Für die meisten Berechnungen in Halbleiterbauelementen sind nur
wenige Bänder wichtig:
– die (fast) gefüllten Bänder mit der höchsten Energie
– die (fast) leeren Bänder mit der niedrigsten Energie
• Die Bandstruktur wird dann in einem vereinfachten Bändermodell
dargestellt:
W
=2 k 2
WC (k ) = WG +
2me
WG
WG
WC
WV
=2 k 2
WV = −
2mh
Primitives Bändermodell
• Für die meisten Berechnungen in Halbleiterbauelementen sind nur
wenige Bänder wichtig:
– die (fast) gefüllten Bänder mit der höchsten Energie
– die (fast) leeren Bänder mit der niedrigsten Energie
• Die Bandstruktur wird dann in einem vereinfachten Bändermodell
dargestellt:
WC: Minimum des Leitungsbands
(Conduction band)
WV: Maximum des Valenzbandes
(Valence band)
WG: Energielücke
(Energy gap)
WG
WC
WV
Besetzung der Bänder mit Elektronen
• Die Verteilung von Elektronen auf die Bänder sieht bei Metallen,
Halbleitern und Isolatoren bei Raumtemperatur folgendermaßen aus:
W
Source: B. Van Zeghbroeck
Defektelektronen (Löcher) im Valenzband
• Anstatt die vielen unbeweglichen (im Stau stehenden) Elektronen im
Valenzband zu betrachten, ist es einfacher die wenigen beweglichen
Defektelektronen (Löcher) zu analysieren.
• Fehlende Elektronen im fast vollständig besetzten Valenzband sind
beweglich (Analogie: Wasserblasen, Bierkasten mit einer fehlenden
Flasche, …)
• Löcher können als einzelne Teilchen mit einer positiven Ladung und
• im Vorzeichen geänderter effektiver Masse (positiv wenn
Elektronenmasse negativ !) angesehen werden
Berechnung der Leitfähigkeit
• Quantitativ wird die Leitfähigkeit σ berechnet durch:
Anzahl der
Defektelektronen
im Valenzband
Ladung des Elektrons
Beweglichkeit der
Ladungsträger im
Leitungsband
Anzahl der
Ladungsträger im
Leitungsband
Beweglichkeit der
Ladungsträger im
Valenzband
• Wie kommen die Elektronen bei Halbleitern eigentlich ins
Leitungsband und wie viele gibt es dort?