Übungsblatt 3

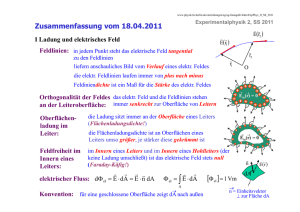
Übungsblatt 2
zur Vorlesung EP2 (Prof. Grüner) im SS 2011
20. Mai 2010
Aufgabe 1: Feldlinien
a) Richtig oder falsch?
• Das elektrische Feld einer Punktladung zeigt immer von der Ladung
weg.
Falsch! Bei negativen Ladungen zeigen die Feldlinien hin.
• Alle makroskopishcen Ladungen q können als q = ±ne geschrieben
werden, wobei n eine ganze Zahl und e die Ladung des Elektrons ist.
Richtig!
• Elektrische Feldlinien divergieren niemals von einem Raumpunkt.
Falsch! Feldlinien divergieren immer von der positiven Ladung.
• Elektrische Feldlinien kreuzen sich nie in einem Raumpunkt.
Richtig! Feldlinien zeigen in die Richtung der Kraft und die muÿ eindeutig sein.
• Alle Moleküle haben in Gegenwart eines äuÿeren elektrischen Feldes
elektrische Dipolmomente.
Richtig!
b) Zwei gleich groÿe positive Ladungen benden sich in kleinem Abstand
voneinander. Skizzieren Sie sowohl die Äquipotentiallinien als auch die Feldlinien.
Lösung: Abbildung ?? c) ist richtig
Aufgabe 2: Elektrisches Feld einer geladenen Linie
Gegeben ist eine geladene Linie mit der konstanten Linienladungsdichte λ
und der Länge l, die auf der x-Achse liegt. Berechnen Sie die y-Komponente
des elektrischen Feldes an einem Punkt P der im Abstand d senkrecht über
dem Mittelpunkt der Linie liegt.
1
Abbildung 1: Rot - Equipotentiallinien
Lösung:
Das Koordinatensystem wird so gewählt, daÿ der Ursprung mit der Mitte der Ladungsverteilung übereinstimmt und die Linienladung selbst auf
der x-Achse liegt (siehe Abbildung ??). Das Feld besitzt eine x- und eine
y-Komponente allerdings existiert aus Symmetriegründen für jedes rechts
des Ursprungs liegende Ladungselement ein entsprechendes Ladungselement
~
links des Ursprungs. Dadurch heben sich die x-Komponenten des Feldes dE
~ ) brau~ (Integration über die Feldelemente dE
auf. Bei der Berechnung von E
chen daher nur die y-Komponenten berücksichtigt werden.
Die Stärke des Feldes, das durch ein Ladungselement dq = λdx erzeugt
wird, ist:
|dE| =
1 λdx
1 dq
=
2
4π0 r
4π0 r2
(1)
Die y-Komponente des Feldes ist:
dEy =
1 λdx
cosΘ
4π0 r2
(2)
Das Gesamtfeld Ey der Linienladung mit der Länge l erhält man durch Integration entlang der Geraden von x = − 21 l bis x = + 21 l. Wegen der Symmetrie
2
Abbildung 2: Skizze zu Aufgabe 2)
der Ladungsverteilung genügt es, von x = 0 bis x = 21 l zu integrieren und
das Resultat zu verdoppeln:
x=+ 12 l
x=+ 21 l
Z
Z
dEy = 2
Ey =
dEy
(3)
x=0
x=− 12 l
Ersetzt man die Variable x durch Θ, so vereinfacht sich die Integration. Die
Ortsvariablen x und y hängen mit dem Winkel Θ über
x = y tanΘ
(4)
zusammen, wobei y den Abstand von P zur Linienladung angibt. Wir erhal3
ten:
1
dx
=y 2 =y
dΘ
cos Θ
2
r
.
y
(5)
Der Zuwachs dx steht somit durch dx = ry dΘ mit dem Zuwachs dΘ in
2
Beziehung. Ersetzt man in Gleichung (??) dx durch ry dΘ, so ist:
2
dEy =
1 λ
cos ΘdΘ.
4π0 y
(6)
Gleichung (??) ergibt Θ = 0 für x = 0 und Θ = Θ0 für x = 21 l. Es gilt:
tan Θ0 =
1
l
2
y
(7)
.
Integration der Gleichung (??) von Θ = 0 bis Θ = Θ0 und Verdoppelung des
Ergebnisses ergibt die gesamte y-Komponente des Feldes:
1 λ
Ey =
2π0 y
ZΘ0
(8)
cos ΘdΘ,
0
oder
1 λ
1 λ
q
Ey =
sin Θ0 =
2π0 y
2π0 y
1
l
2
1 2
l
2
,
(9)
+ y2
wobei sin Θ0 mit l und y durch:
sin Θ0 = q
1
l
2
1 2
l
2
(10)
+
y2
verknüpft ist. Ist y sehr viel gröÿer als l, so ergibt sich als Näherung:
sin Θ≈
1
l
2
y
für y l,
(11)
und Ey beträgt dann angenähert:
Ey ≈
1 λl
1 Q
=
,
2
4π0 y
4π0 y 2
(12)
wobei Q = λl die Gesamtladung ist. Wie erwartet, wirkt die endliche Linienladung in groÿer Entfernung wie eine Punktladung.
4
Aufgabe 3: Potentielle Energie von Punktladungen
Drei Punktladungen der Werte 1 C, 2 C und 3 C benden sich an den Ecken
eines gleichseiteigen Dreiecks mit Kantenlänge 1 m. Welche Arbeit muss man
aufwenden, um die drei Ladungen zu einem gleichseitigen Dreieck mit halber
Kantenlänge zusammenzuschieben?
Lösung:
Betrachte Ausgangskonguration: Wieviel Energie steckt schon im System?
Erste Ladung sei da. Zweite Ladung zur ersten bringen:
Z
Epot = −
Z1m
∆Epot,1 = −
∞
~
F~ dl
1 1C · 2C
1
dr =
2
4π0 r
4π0
1C · 2C
1m
(13)
Dritte Ladung kommt dazu:
Z1m
∆Epot,2
Z1m
1 1C · 3C
1 2C · 3C
= −
dr −
dr
2
4π0 r
4π0 r2
∞
∞
1C · 3C
1
2C · 3C
1
+
=
4π0
1m
4π0
1m
⇒ ∆Epot,ges = ∆Epot,1 + ∆Epot,2 =
11 2
C /m.
4π0
(14)
(15)
(16)
→ Halbe Kantenlänge → 1m wird zu 0.5m → Energie verdoppelt sich. Daraus
folgt, daÿ nochmals ∆Epot,ges aufgewendet werden muÿ.
Besprechung der Aufgaben am 27.05.11