Astronomie und Astrophysik I, 7

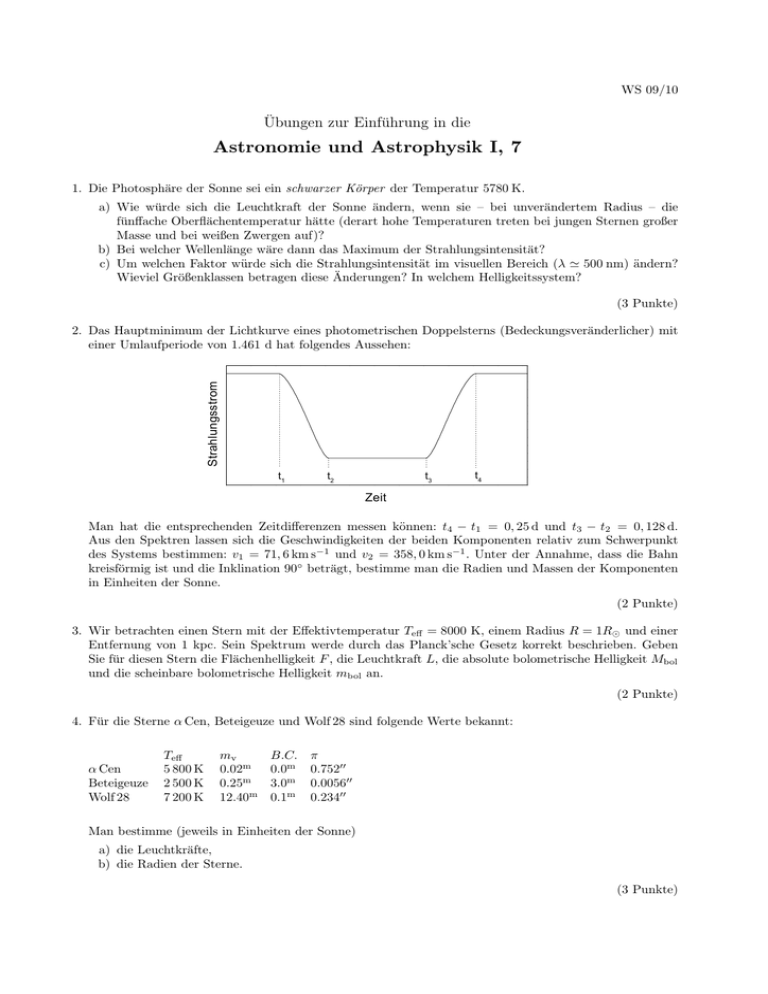
WS 09/10
Übungen zur Einführung in die
Astronomie und Astrophysik I, 7
1. Die Photosphäre der Sonne sei ein schwarzer Körper der Temperatur 5780 K.
a) Wie würde sich die Leuchtkraft der Sonne ändern, wenn sie – bei unverändertem Radius – die
fünffache Oberflächentemperatur hätte (derart hohe Temperaturen treten bei jungen Sternen großer
Masse und bei weißen Zwergen auf)?
b) Bei welcher Wellenlänge wäre dann das Maximum der Strahlungsintensität?
c) Um welchen Faktor würde sich die Strahlungsintensität im visuellen Bereich (λ ' 500 nm) ändern?
Wieviel Größenklassen betragen diese Änderungen? In welchem Helligkeitssystem?
(3 Punkte)
Strahlungsstrom
2. Das Hauptminimum der Lichtkurve eines photometrischen Doppelsterns (Bedeckungsveränderlicher) mit
einer Umlaufperiode von 1.461 d hat folgendes Aussehen:
t1
t2
t3
t4
Zeit
Man hat die entsprechenden Zeitdifferenzen messen können: t4 − t1 = 0, 25 d und t3 − t2 = 0, 128 d.
Aus den Spektren lassen sich die Geschwindigkeiten der beiden Komponenten relativ zum Schwerpunkt
des Systems bestimmen: v1 = 71, 6 km s−1 und v2 = 358, 0 km s−1 . Unter der Annahme, dass die Bahn
kreisförmig ist und die Inklination 90◦ beträgt, bestimme man die Radien und Massen der Komponenten
in Einheiten der Sonne.
(2 Punkte)
3. Wir betrachten einen Stern mit der Effektivtemperatur Teff = 8000 K, einem Radius R = 1R¯ und einer
Entfernung von 1 kpc. Sein Spektrum werde durch das Planck’sche Gesetz korrekt beschrieben. Geben
Sie für diesen Stern die Flächenhelligkeit F , die Leuchtkraft L, die absolute bolometrische Helligkeit Mbol
und die scheinbare bolometrische Helligkeit mbol an.
(2 Punkte)
4. Für die Sterne α Cen, Beteigeuze und Wolf 28 sind folgende Werte bekannt:
α Cen
Beteigeuze
Wolf 28
Teff
5 800 K
2 500 K
7 200 K
mv
0.02m
0.25m
12.40m
B.C.
0.0m
3.0m
0.1m
π
0.75200
0.005600
0.23400
Man bestimme (jeweils in Einheiten der Sonne)
a) die Leuchtkräfte,
b) die Radien der Sterne.
(3 Punkte)